Nearly Linear Sparsification of $\ell_p$ Subspace Approximation

The $\ell_p$ subspace approximation problem is an NP-hard low rank approximation problem that generalizes the median hyperplane problem ($p = 1$), principal component analysis ($p = 2$), and the center hyperplane problem ($p = \infty$). A popular approach to cope with the NP-hardness of this problem is to compute a strong coreset, which is a small weighted subset of the input points which simultaneously approximates the cost of every $k$-dimensional subspace, typically to $(1+\varepsilon)$ relative error for a small constant $\varepsilon$. We obtain the first algorithm for constructing a strong coreset for $\ell_p$ subspace approximation with a nearly optimal dependence on the rank parameter $k$, obtaining a nearly linear bound of $\tilde O(k)\mathrm{poly}(\varepsilon^{-1})$ for $p<2$ and $\tilde O(k^{p/2})\mathrm{poly}(\varepsilon^{-1})$ for $p>2$. Prior constructions either achieved a similar size bound but produced a coreset with a modification of the original points [SW18, FKW21], or produced a coreset of the original points but lost $\mathrm{poly}(k)$ factors in the coreset size [HV20, WY23]. Our techniques also lead to the first nearly optimal online strong coresets for $\ell_p$ subspace approximation with similar bounds as the offline setting, resolving a problem of [WY23]. All prior approaches lose $\mathrm{poly}(k)$ factors in this setting, even when allowed to modify the original points.

Reweighted Solutions for Weighted Low Rank Approximation

Weighted low rank approximation (WLRA) is an important yet computationally challenging primitive with applications ranging from statistical analysis, model compression, and signal processing. To cope with the NP-hardness of this problem, prior work considers heuristics, bicriteria, or fixed parameter tractable algorithms to solve this problem. In this work, we introduce a new relaxed solution to WLRA which outputs a matrix that is not necessarily low rank, but can be stored using very few parameters and gives provable approximation guarantees when the weight matrix has low rank. Our central idea is to use the weight matrix itself to reweight a low rank solution, which gives an extremely simple algorithm with remarkable empirical performance in applications to model compression and on synthetic datasets. Our algorithm also gives nearly optimal communication complexity bounds for a natural distributed problem associated with this problem, for which we show matching communication lower bounds. Together, our communication complexity bounds show that the rank of the weight matrix provably parameterizes the communication complexity of WLRA. We also obtain the first relative error guarantees for feature selection with a weighted objective.

SequentialAttention++ for Block Sparsification: Differentiable Pruning Meets Combinatorial Optimization

Neural network pruning is a key technique towards engineering large yet scalable, interpretable, and generalizable models. Prior work on the subject has developed largely along two orthogonal directions: (1) differentiable pruning for efficiently and accurately scoring the importance of parameters, and (2) combinatorial optimization for efficiently searching over the space of sparse models. We unite the two approaches, both theoretically and empirically, to produce a coherent framework for structured neural network pruning in which differentiable pruning guides combinatorial optimization algorithms to select the most important sparse set of parameters. Theoretically, we show how many existing differentiable pruning techniques can be understood as nonconvex regularization for group sparse optimization, and prove that for a wide class of nonconvex regularizers, the global optimum is unique, group-sparse, and provably yields an approximate solution to a sparse convex optimization problem. The resulting algorithm that we propose, SequentialAttention++, advances the state of the art in large-scale neural network block-wise pruning tasks on the ImageNet and Criteo datasets.

Sketching Algorithms for Sparse Dictionary Learning: PTAS and Turnstile Streaming

Sketching algorithms have recently proven to be a powerful approach both for designing low-space streaming algorithms as well as fast polynomial time approximation schemes (PTAS). In this work, we develop new techniques to extend the applicability of sketching-based approaches to the sparse dictionary learning and the Euclidean $k$-means clustering problems. In particular, we initiate the study of the challenging setting where the dictionary/clustering assignment for each of the $n$ input points must be output, which has surprisingly received little attention in prior work. On the fast algorithms front, we obtain a new approach for designing PTAS's for the $k$-means clustering problem, which generalizes to the first PTAS for the sparse dictionary learning problem. On the streaming algorithms front, we obtain new upper bounds and lower bounds for dictionary learning and $k$-means clustering. In particular, given a design matrix $\mathbf A\in\mathbb R^{n\times d}$ in a turnstile stream, we show an $\tilde O(nr/\epsilon^2 + dk/\epsilon)$ space upper bound for $r$-sparse dictionary learning of size $k$, an $\tilde O(n/\epsilon^2 + dk/\epsilon)$ space upper bound for $k$-means clustering, as well as an $\tilde O(n)$ space upper bound for $k$-means clustering on random order row insertion streams with a natural "bounded sensitivity" assumption. On the lower bounds side, we obtain a general $\tilde\Omega(n/\epsilon + dk/\epsilon)$ lower bound for $k$-means clustering, as well as an $\tilde\Omega(n/\epsilon^2)$ lower bound for algorithms which can estimate the cost of a single fixed set of candidate centers.

Performance of $\ell_1$ Regularization for Sparse Convex Optimization

Despite widespread adoption in practice, guarantees for the LASSO and Group LASSO are strikingly lacking in settings beyond statistical problems, and these algorithms are usually considered to be a heuristic in the context of sparse convex optimization on deterministic inputs. We give the first recovery guarantees for the Group LASSO for sparse convex optimization with vector-valued features. We show that if a sufficiently large Group LASSO regularization is applied when minimizing a strictly convex function $l$, then the minimizer is a sparse vector supported on vector-valued features with the largest $\ell_2$ norm of the gradient. Thus, repeating this procedure selects the same set of features as the Orthogonal Matching Pursuit algorithm, which admits recovery guarantees for any function $l$ with restricted strong convexity and smoothness via weak submodularity arguments. This answers open questions of Tibshirani et al. and Yasuda et al. Our result is the first to theoretically explain the empirical success of the Group LASSO for convex functions under general input instances assuming only restricted strong convexity and smoothness. Our result also generalizes provable guarantees for the Sequential Attention algorithm, which is a feature selection algorithm inspired by the attention mechanism proposed by Yasuda et al. As an application of our result, we give new results for the column subset selection problem, which is well-studied when the loss is the Frobenius norm or other entrywise matrix losses. We give the first result for general loss functions for this problem that requires only restricted strong convexity and smoothness.

Sharper Bounds for $\ell_p$ Sensitivity Sampling

In large scale machine learning, random sampling is a popular way to approximate datasets by a small representative subset of examples. In particular, sensitivity sampling is an intensely studied technique which provides provable guarantees on the quality of approximation, while reducing the number of examples to the product of the VC dimension $d$ and the total sensitivity $\mathfrak S$ in remarkably general settings. However, guarantees going beyond this general bound of $\mathfrak S d$ are known in perhaps only one setting, for $\ell_2$ subspace embeddings, despite intense study of sensitivity sampling in prior work. In this work, we show the first bounds for sensitivity sampling for $\ell_p$ subspace embeddings for $p\neq 2$ that improve over the general $\mathfrak S d$ bound, achieving a bound of roughly $\mathfrak S^{2/p}$ for $1\leq p<2$ and $\mathfrak S^{2-2/p}$ for $2<p<\infty$. For $1\leq p<2$, we show that this bound is tight, in the sense that there exist matrices for which $\mathfrak S^{2/p}$ samples is necessary. Furthermore, our techniques yield further new results in the study of sampling algorithms, showing that the root leverage score sampling algorithm achieves a bound of roughly $d$ for $1\leq p<2$, and that a combination of leverage score and sensitivity sampling achieves an improved bound of roughly $d^{2/p}\mathfrak S^{2-4/p}$ for $2<p<\infty$. Our sensitivity sampling results yield the best known sample complexity for a wide class of structured matrices that have small $\ell_p$ sensitivity.

Sequential Attention for Feature Selection

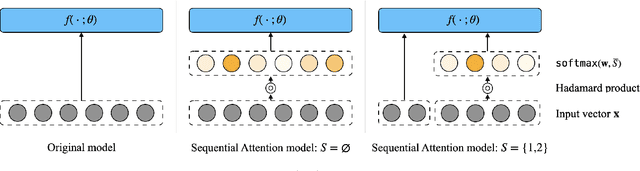
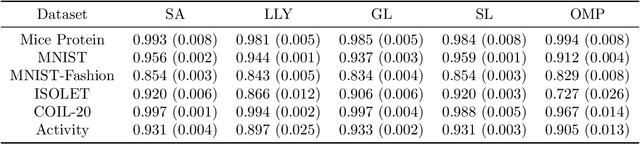
Feature selection is the problem of selecting a subset of features for a machine learning model that maximizes model quality subject to a resource budget constraint. For neural networks, prior methods, including those based on $\ell_1$ regularization, attention, and stochastic gates, typically select all of the features in one evaluation round, ignoring the residual value of the features during selection (i.e., the marginal contribution of a feature conditioned on the previously selected features). We propose a feature selection algorithm called Sequential Attention that achieves state-of-the-art empirical results for neural networks. This algorithm is based on an efficient implementation of greedy forward selection and uses attention weights at each step as a proxy for marginal feature importance. We provide theoretical insights into our Sequential Attention algorithm for linear regression models by showing that an adaptation to this setting is equivalent to the classical Orthogonal Matching Pursuit algorithm [PRK1993], and thus inherits all of its provable guarantees. Lastly, our theoretical and empirical analyses provide new explanations towards the effectiveness of attention and its connections to overparameterization, which might be of independent interest.

Online Lewis Weight Sampling

The seminal work of Cohen and Peng introduced Lewis weight sampling to the theoretical computer science community, yielding fast row sampling algorithms for approximating $d$-dimensional subspaces of $\ell_p$ up to $(1+\epsilon)$ error. Several works have extended this important primitive to other settings, including the online coreset, sliding window, and adversarial streaming models. However, these results are only for $p\in\{1,2\}$, and results for $p=1$ require a suboptimal $\tilde O(d^2/\epsilon^2)$ samples. In this work, we design the first nearly optimal $\ell_p$ subspace embeddings for all $p\in(0,\infty)$ in the online coreset, sliding window, and the adversarial streaming models. In all three models, our algorithms store $\tilde O(d^{1\lor(p/2)}/\epsilon^2)$ rows. This answers a substantial generalization of the main open question of [BDMMUWZ2020], and gives the first results for all $p\notin\{1,2\}$. Towards our result, we give the first analysis of "one-shot'' Lewis weight sampling of sampling rows proportionally to their Lewis weights, with sample complexity $\tilde O(d^{p/2}/\epsilon^2)$ for $p>2$. Previously, this scheme was only known to have sample complexity $\tilde O(d^{p/2}/\epsilon^5)$, whereas $\tilde O(d^{p/2}/\epsilon^2)$ is known if a more sophisticated recursive sampling is used. The recursive sampling cannot be implemented online, thus necessitating an analysis of one-shot Lewis weight sampling. Our analysis uses a novel connection to online numerical linear algebra. As an application, we obtain the first one-pass streaming coreset algorithms for $(1+\epsilon)$ approximation of important generalized linear models, such as logistic regression and $p$-probit regression. Our upper bounds are parameterized by a complexity parameter $\mu$ introduced by [MSSW2018], and we show the first lower bounds showing that a linear dependence on $\mu$ is necessary.

Active Sampling for Linear Regression Beyond the $\ell_2$ Norm

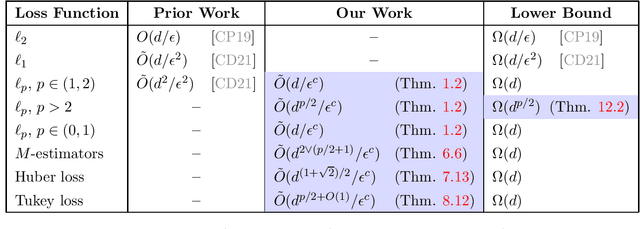
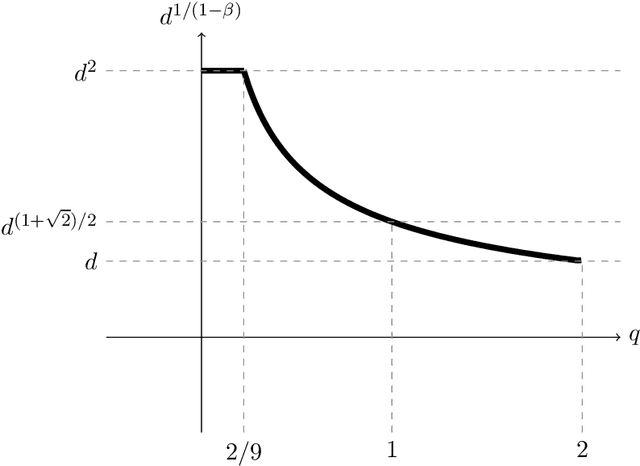
We study active sampling algorithms for linear regression, which aim to query only a small number of entries of a target vector $b\in\mathbb{R}^n$ and output a near minimizer to $\min_{x\in\mathbb{R}^d}\|Ax-b\|$, where $A\in\mathbb{R}^{n \times d}$ is a design matrix and $\|\cdot\|$ is some loss function. For $\ell_p$ norm regression for any $0<p<\infty$, we give an algorithm based on Lewis weight sampling that outputs a $(1+\epsilon)$ approximate solution using just $\tilde{O}(d^{\max(1,{p/2})}/\mathrm{poly}(\epsilon))$ queries to $b$. We show that this dependence on $d$ is optimal, up to logarithmic factors. Our result resolves a recent open question of Chen and Derezi\'{n}ski, who gave near optimal bounds for the $\ell_1$ norm, and suboptimal bounds for $\ell_p$ regression with $p\in(1,2)$. We also provide the first total sensitivity upper bound of $O(d^{\max\{1,p/2\}}\log^2 n)$ for loss functions with at most degree $p$ polynomial growth. This improves a recent result of Tukan, Maalouf, and Feldman. By combining this with our techniques for the $\ell_p$ regression result, we obtain an active regression algorithm making $\tilde O(d^{1+\max\{1,p/2\}}/\mathrm{poly}(\epsilon))$ queries, answering another open question of Chen and Derezi\'{n}ski. For the important special case of the Huber loss, we further improve our bound to an active sample complexity of $\tilde O(d^{(1+\sqrt2)/2}/\epsilon^c)$ and a non-active sample complexity of $\tilde O(d^{4-2\sqrt 2}/\epsilon^c)$, improving a previous $d^4$ bound for Huber regression due to Clarkson and Woodruff. Our sensitivity bounds have further implications, improving a variety of previous results using sensitivity sampling, including Orlicz norm subspace embeddings and robust subspace approximation. Finally, our active sampling results give the first sublinear time algorithms for Kronecker product regression under every $\ell_p$ norm.

Tight Kernel Query Complexity of Kernel Ridge Regression and Kernel $k$-means Clustering

We present tight lower bounds on the number of kernel evaluations required to approximately solve kernel ridge regression (KRR) and kernel $k$-means clustering (KKMC) on $n$ input points. For KRR, our bound for relative error approximation to the minimizer of the objective function is $\Omega(nd_{\mathrm{eff}}^\lambda/\varepsilon)$ where $d_{\mathrm{eff}}^\lambda$ is the effective statistical dimension, which is tight up to a $\log(d_{\mathrm{eff}}^\lambda/\varepsilon)$ factor. For KKMC, our bound for finding a $k$-clustering achieving a relative error approximation of the objective function is $\Omega(nk/\varepsilon)$, which is tight up to a $\log(k/\varepsilon)$ factor. Our KRR result resolves a variant of an open question of El Alaoui and Mahoney, asking whether the effective statistical dimension is a lower bound on the sampling complexity or not. Furthermore, for the important practical case when the input is a mixture of Gaussians, we provide a KKMC algorithm which bypasses the above lower bound.