A Polynomial-Time Algorithm for Variational Inequalities under the Minty Condition

Solving (Stampacchia) variational inequalities (SVIs) is a foundational problem at the heart of optimization, with a host of critical applications ranging from engineering to economics. However, this expressivity comes at the cost of computational hardness. As a result, most research has focused on carving out specific subclasses that elude those intractability barriers. A classical property that goes back to the 1960s is the Minty condition, which postulates that the Minty VI (MVI) problem -- the weak dual of the SVI problem -- admits a solution. In this paper, we establish the first polynomial-time algorithm -- that is, with complexity growing polynomially in the dimension $d$ and $\log(1/\epsilon)$ -- for solving $\epsilon$-SVIs for Lipschitz continuous mappings under the Minty condition. Prior approaches either incurred an exponentially worse dependence on $1/\epsilon$ (and other natural parameters of the problem) or made overly restrictive assumptions -- such as strong monotonicity. To do so, we introduce a new variant of the ellipsoid algorithm wherein separating hyperplanes are obtained after taking a gradient descent step from the center of the ellipsoid. It succeeds even though the set of SVIs can be nonconvex and not fully dimensional. Moreover, when our algorithm is applied to an instance with no MVI solution and fails to identify an SVI solution, it produces a succinct certificate of MVI infeasibility. We also show that deciding whether the Minty condition holds is $\mathsf{coNP}$-complete. We provide several extensions and new applications of our main results. Specifically, we obtain the first polynomial-time algorithms for i) solving monotone VIs, ii) globally minimizing a (potentially nonsmooth) quasar-convex function, and iii) computing Nash equilibria in multi-player harmonic games.

Learning and Computation of $Φ$-Equilibria at the Frontier of Tractability

$\Phi$-equilibria -- and the associated notion of $\Phi$-regret -- are a powerful and flexible framework at the heart of online learning and game theory, whereby enriching the set of deviations $\Phi$ begets stronger notions of rationality. Recently, Daskalakis, Farina, Fishelson, Pipis, and Schneider (STOC '24) -- abbreviated as DFFPS -- settled the existence of efficient algorithms when $\Phi$ contains only linear maps under a general, $d$-dimensional convex constraint set $\mathcal{X}$. In this paper, we significantly extend their work by resolving the case where $\Phi$ is $k$-dimensional; degree-$\ell$ polynomials constitute a canonical such example with $k = d^{O(\ell)}$. In particular, positing only oracle access to $\mathcal{X}$, we obtain two main positive results: i) a $\text{poly}(n, d, k, \text{log}(1/\epsilon))$-time algorithm for computing $\epsilon$-approximate $\Phi$-equilibria in $n$-player multilinear games, and ii) an efficient online algorithm that incurs average $\Phi$-regret at most $\epsilon$ using $\text{poly}(d, k)/\epsilon^2$ rounds. We also show nearly matching lower bounds in the online learning setting, thereby obtaining for the first time a family of deviations that captures the learnability of $\Phi$-regret. From a technical standpoint, we extend the framework of DFFPS from linear maps to the more challenging case of maps with polynomial dimension. At the heart of our approach is a polynomial-time algorithm for computing an expected fixed point of any $\phi : \mathcal{X} \to \mathcal{X}$ based on the ellipsoid against hope (EAH) algorithm of Papadimitriou and Roughgarden (JACM '08). In particular, our algorithm for computing $\Phi$-equilibria is based on executing EAH in a nested fashion -- each step of EAH itself being implemented by invoking a separate call to EAH.

Expected Variational Inequalities

Variational inequalities (VIs) encompass many fundamental problems in diverse areas ranging from engineering to economics and machine learning. However, their considerable expressivity comes at the cost of computational intractability. In this paper, we introduce and analyze a natural relaxation -- which we refer to as expected variational inequalities (EVIs) -- where the goal is to find a distribution that satisfies the VI constraint in expectation. By adapting recent techniques from game theory, we show that, unlike VIs, EVIs can be solved in polynomial time under general (nonmonotone) operators. EVIs capture the seminal notion of correlated equilibria, but enjoy a greater reach beyond games. We also employ our framework to capture and generalize several existing disparate results, including from settings such as smooth games, and games with coupled constraints or nonconcave utilities.

Computing Game Symmetries and Equilibria That Respect Them

Strategic interactions can be represented more concisely, and analyzed and solved more efficiently, if we are aware of the symmetries within the multiagent system. Symmetries also have conceptual implications, for example for equilibrium selection. We study the computational complexity of identifying and using symmetries. Using the classical framework of normal-form games, we consider game symmetries that can be across some or all players and/or actions. We find a strong connection between game symmetries and graph automorphisms, yielding graph automorphism and graph isomorphism completeness results for characterizing the symmetries present in a game. On the other hand, we also show that the problem becomes polynomial-time solvable when we restrict the consideration of actions in one of two ways. Next, we investigate when exactly game symmetries can be successfully leveraged for Nash equilibrium computation. We show that finding a Nash equilibrium that respects a given set of symmetries is PPAD- and CLS-complete in general-sum and team games respectively -- that is, exactly as hard as Brouwer fixed point and gradient descent problems. Finally, we present polynomial-time methods for the special cases where we are aware of a vast number of symmetries, or where the game is two-player zero-sum and we do not even know the symmetries.

Imperfect-Recall Games: Equilibrium Concepts and Their Complexity

We investigate optimal decision making under imperfect recall, that is, when an agent forgets information it once held before. An example is the absentminded driver game, as well as team games in which the members have limited communication capabilities. In the framework of extensive-form games with imperfect recall, we analyze the computational complexities of finding equilibria in multiplayer settings across three different solution concepts: Nash, multiselves based on evidential decision theory (EDT), and multiselves based on causal decision theory (CDT). We are interested in both exact and approximate solution computation. As special cases, we consider (1) single-player games, (2) two-player zero-sum games and relationships to maximin values, and (3) games without exogenous stochasticity (chance nodes). We relate these problems to the complexity classes P, PPAD, PLS, $\Sigma_2^P$ , $\exists$R, and $\exists \forall$R.

Sparsified Linear Programming for Zero-Sum Equilibrium Finding

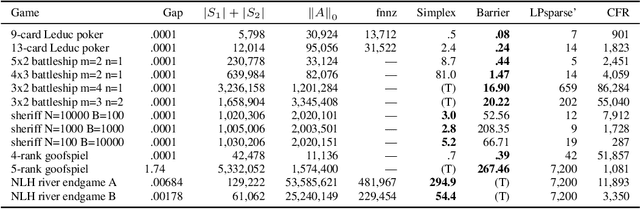
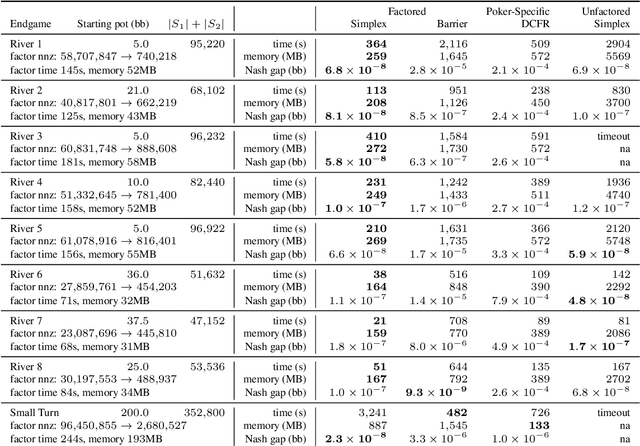
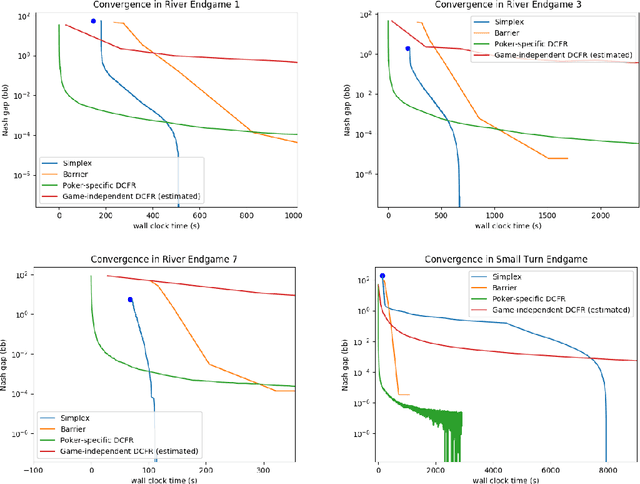
Computational equilibrium finding in large zero-sum extensive-form imperfect-information games has led to significant recent AI breakthroughs. The fastest algorithms for the problem are new forms of counterfactual regret minimization [Brown and Sandholm, 2019]. In this paper we present a totally different approach to the problem, which is competitive and often orders of magnitude better than the prior state of the art. The equilibrium-finding problem can be formulated as a linear program (LP) [Koller et al., 1994], but solving it as an LP has not been scalable due to the memory requirements of LP solvers, which can often be quadratically worse than CFR-based algorithms. We give an efficient practical algorithm that factors a large payoff matrix into a product of two matrices that are typically dramatically sparser. This allows us to express the equilibrium-finding problem as a linear program with size only a logarithmic factor worse than CFR, and thus allows linear program solvers to run on such games. With experiments on poker endgames, we demonstrate in practice, for the first time, that modern linear program solvers are competitive against even game-specific modern variants of CFR in solving large extensive-form games, and can be used to compute exact solutions unlike iterative algorithms like CFR.

A Spectral View of Adversarially Robust Features

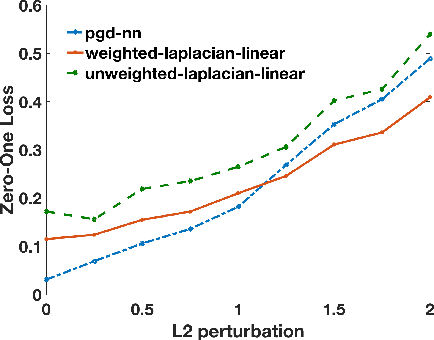
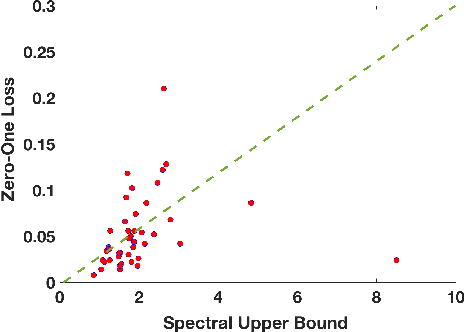
Given the apparent difficulty of learning models that are robust to adversarial perturbations, we propose tackling the simpler problem of developing adversarially robust features. Specifically, given a dataset and metric of interest, the goal is to return a function (or multiple functions) that 1) is robust to adversarial perturbations, and 2) has significant variation across the datapoints. We establish strong connections between adversarially robust features and a natural spectral property of the geometry of the dataset and metric of interest. This connection can be leveraged to provide both robust features, and a lower bound on the robustness of any function that has significant variance across the dataset. Finally, we provide empirical evidence that the adversarially robust features given by this spectral approach can be fruitfully leveraged to learn a robust (and accurate) model.

Mitigating Unwanted Biases with Adversarial Learning

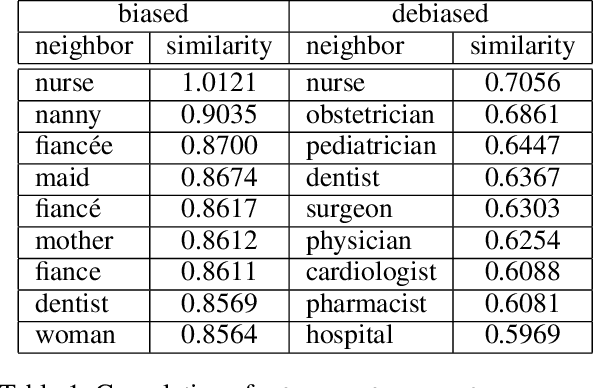
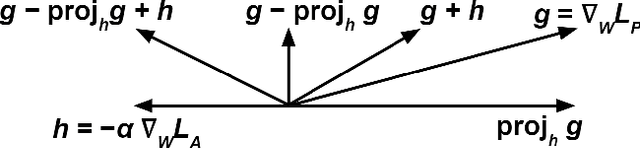
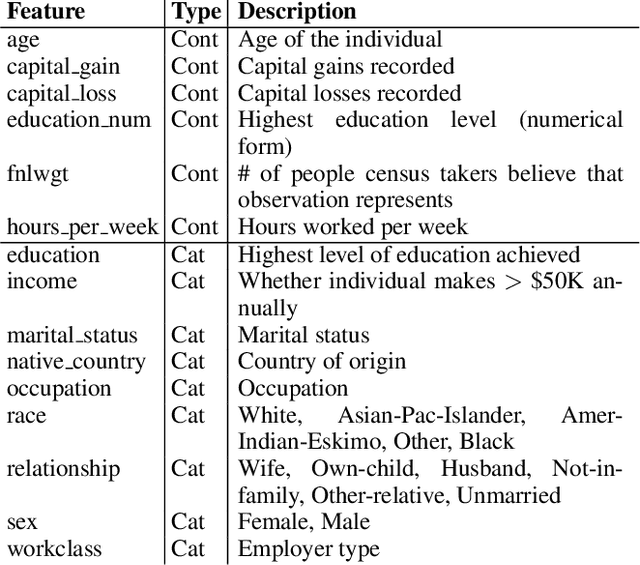
Machine learning is a tool for building models that accurately represent input training data. When undesired biases concerning demographic groups are in the training data, well-trained models will reflect those biases. We present a framework for mitigating such biases by including a variable for the group of interest and simultaneously learning a predictor and an adversary. The input to the network X, here text or census data, produces a prediction Y, such as an analogy completion or income bracket, while the adversary tries to model a protected variable Z, here gender or zip code. The objective is to maximize the predictor's ability to predict Y while minimizing the adversary's ability to predict Z. Applied to analogy completion, this method results in accurate predictions that exhibit less evidence of stereotyping Z. When applied to a classification task using the UCI Adult (Census) Dataset, it results in a predictive model that does not lose much accuracy while achieving very close to equality of odds (Hardt, et al., 2016). The method is flexible and applicable to multiple definitions of fairness as well as a wide range of gradient-based learning models, including both regression and classification tasks.