Polynomial Time Reinforcement Learning in Correlated FMDPs with Linear Value Functions

Many reinforcement learning (RL) environments in practice feature enormous state spaces that may be described compactly by a "factored" structure, that may be modeled by Factored Markov Decision Processes (FMDPs). We present the first polynomial-time algorithm for RL with FMDPs that does not rely on an oracle planner, and instead of requiring a linear transition model, only requires a linear value function with a suitable local basis with respect to the factorization. With this assumption, we can solve FMDPs in polynomial time by constructing an efficient separation oracle for convex optimization. Importantly, and in contrast to prior work, we do not assume that the transitions on various factors are independent.

Safe Learning of Lifted Action Models

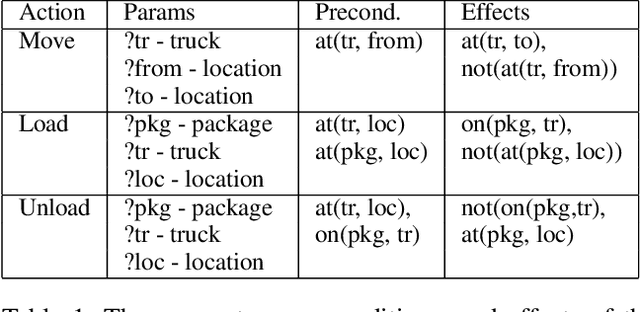
Creating a domain model, even for classical, domain-independent planning, is a notoriously hard knowledge-engineering task. A natural approach to solve this problem is to learn a domain model from observations. However, model learning approaches frequently do not provide safety guarantees: the learned model may assume actions are applicable when they are not, and may incorrectly capture actions' effects. This may result in generating plans that will fail when executed. In some domains such failures are not acceptable, due to the cost of failure or inability to replan online after failure. In such settings, all learning must be done offline, based on some observations collected, e.g., by some other agents or a human. Through this learning, the task is to generate a plan that is guaranteed to be successful. This is called the model-free planning problem. Prior work proposed an algorithm for solving the model-free planning problem in classical planning. However, they were limited to learning grounded domains, and thus they could not scale. We generalize this prior work and propose the first safe model-free planning algorithm for lifted domains. We prove the correctness of our approach, and provide a statistical analysis showing that the number of trajectories needed to solve future problems with high probability is linear in the potential size of the domain model. We also present experiments on twelve IPC domains showing that our approach is able to learn the real action model in all cases with at most two trajectories.

One Network Fits All? Modular versus Monolithic Task Formulations in Neural Networks

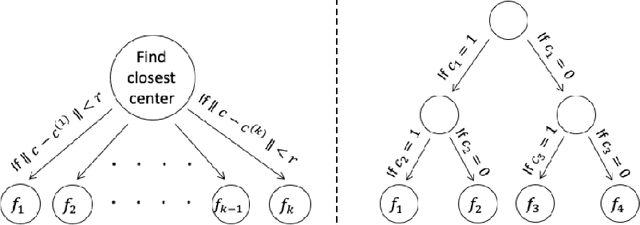
Can deep learning solve multiple tasks simultaneously, even when they are unrelated and very different? We investigate how the representations of the underlying tasks affect the ability of a single neural network to learn them jointly. We present theoretical and empirical findings that a single neural network is capable of simultaneously learning multiple tasks from a combined data set, for a variety of methods for representing tasks -- for example, when the distinct tasks are encoded by well-separated clusters or decision trees over certain task-code attributes. More concretely, we present a novel analysis that shows that families of simple programming-like constructs for the codes encoding the tasks are learnable by two-layer neural networks with standard training. We study more generally how the complexity of learning such combined tasks grows with the complexity of the task codes; we find that combining many tasks may incur a sample complexity penalty, even though the individual tasks are easy to learn. We provide empirical support for the usefulness of the learning bounds by training networks on clusters, decision trees, and SQL-style aggregation.

Probabilistic Generating Circuits

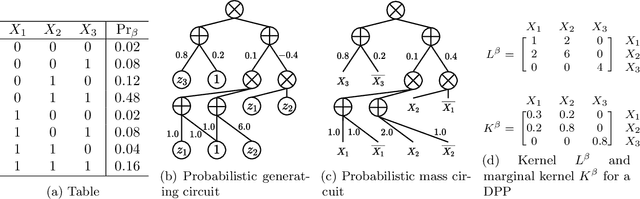
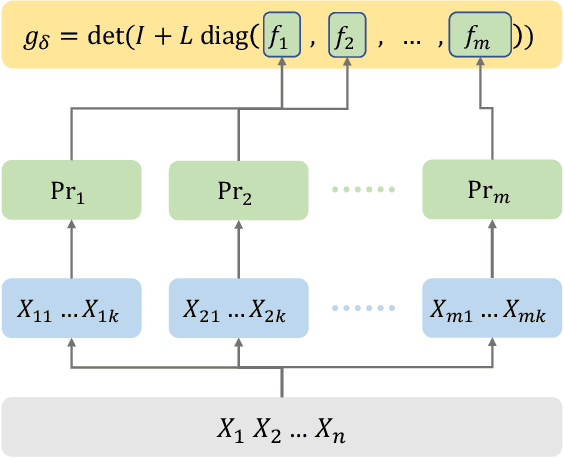
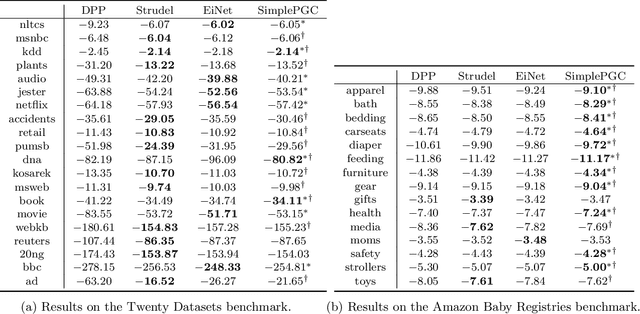
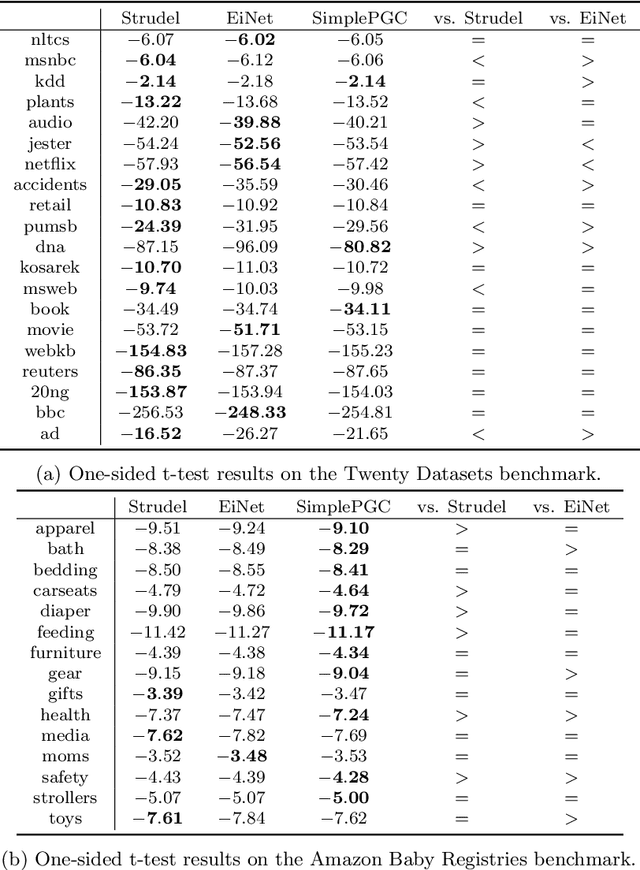
Generating functions, which are widely used in combinatorics and probability theory, encode function values into the coefficients of a polynomial. In this paper, we explore their use as a tractable probabilistic model, and propose probabilistic generating circuits (PGCs) for their efficient representation. PGCs strictly subsume many existing tractable probabilistic models, including determinantal point processes (DPPs), probabilistic circuits (PCs) such as sum-product networks, and tractable graphical models. We contend that PGCs are not just a theoretical framework that unifies vastly different existing models, but also show huge potential in modeling realistic data. We exhibit a simple class of PGCs that are not trivially subsumed by simple combinations of PCs and DPPs, and obtain competitive performance on a suite of density estimation benchmarks. We also highlight PGCs' connection to the theory of strongly Rayleigh distributions.

Learning Implicitly with Noisy Data in Linear Arithmetic

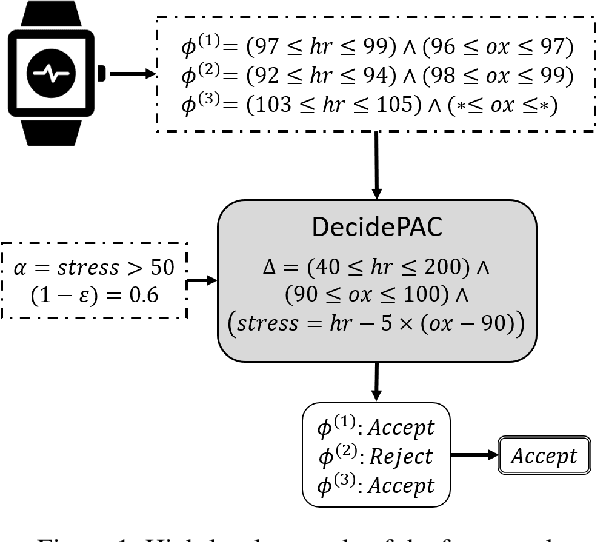
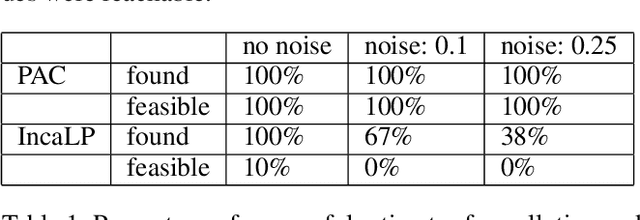
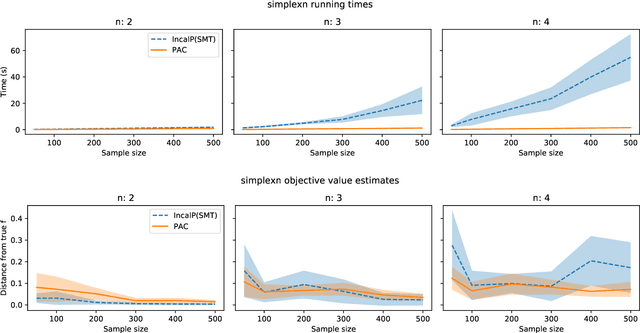
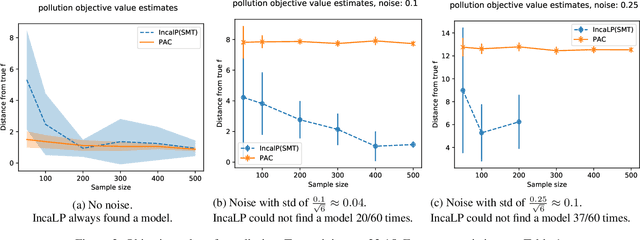
Robustly learning in expressive languages with real-world data continues to be a challenging task. Numerous conventional methods appeal to heuristics without any assurances of robustness. While PAC-Semantics offers strong guarantees, learning explicit representations is not tractable even in a propositional setting. However, recent work on so-called "implicit" learning has shown tremendous promise in terms of obtaining polynomial-time results for fragments of first-order logic. In this work, we extend implicit learning in PAC-Semantics to handle noisy data in the form of intervals and threshold uncertainty in the language of linear arithmetic. We prove that our extended framework keeps the existing polynomial-time complexity guarantees. Furthermore, we provide the first empirical investigation of this hitherto purely theoretical framework. Using benchmark problems, we show that our implicit approach to learning optimal linear programming objective constraints significantly outperforms an explicit approach in practice.

List Learning with Attribute Noise

We introduce and study the model of list learning with attribute noise. Learning with attribute noise was introduced by Shackelford and Volper (COLT 1988) as a variant of PAC learning, in which the algorithm has access to noisy examples and uncorrupted labels, and the goal is to recover an accurate hypothesis. Sloan (COLT 1988) and Goldman and Sloan (Algorithmica 1995) discovered information-theoretic limits to learning in this model, which have impeded further progress. In this article we extend the model to that of list learning, drawing inspiration from the list-decoding model in coding theory, and its recent variant studied in the context of learning. On the positive side, we show that sparse conjunctions can be efficiently list learned under some assumptions on the underlying ground-truth distribution. On the negative side, our results show that even in the list-learning model, efficient learning of parities and majorities is not possible regardless of the representation used.

Query-driven PAC-Learning for Reasoning

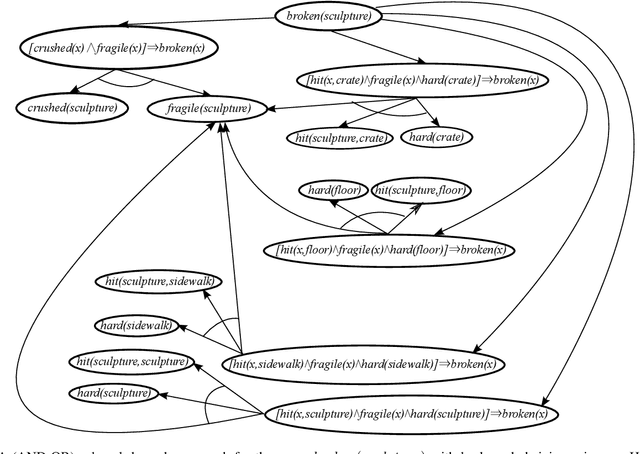
We consider the problem of learning rules from a data set that support a proof of a given query, under Valiant's PAC-Semantics. We show how any backward proof search algorithm that is sufficiently oblivious to the contents of its knowledge base can be modified to learn such rules while it searches for a proof using those rules. We note that this gives such algorithms for standard logics such as chaining and resolution.

Implicitly Learning to Reason in First-Order Logic

We consider the problem of answering queries about formulas of first-order logic based on background knowledge partially represented explicitly as other formulas, and partially represented as examples independently drawn from a fixed probability distribution. PAC semantics, introduced by Valiant, is one rigorous, general proposal for learning to reason in formal languages: although weaker than classical entailment, it allows for a powerful model theoretic framework for answering queries while requiring minimal assumptions about the form of the distribution in question. To date, however, the most significant limitation of that approach, and more generally most machine learning approaches with robustness guarantees, is that the logical language is ultimately essentially propositional, with finitely many atoms. Indeed, the theoretical findings on the learning of relational theories in such generality have been resoundingly negative. This is despite the fact that first-order logic is widely argued to be most appropriate for representing human knowledge. In this work, we present a new theoretical approach to robustly learning to reason in first-order logic, and consider universally quantified clauses over a countably infinite domain. Our results exploit symmetries exhibited by constants in the language, and generalize the notion of implicit learnability to show how queries can be computed against (implicitly) learned first-order background knowledge.

Polynomial-time probabilistic reasoning with partial observations via implicit learning in probability logics

Standard approaches to probabilistic reasoning require that one possesses an explicit model of the distribution in question. But, the empirical learning of models of probability distributions from partial observations is a problem for which efficient algorithms are generally not known. In this work we consider the use of bounded-degree fragments of the "sum-of-squares" logic as a probability logic. Prior work has shown that we can decide refutability for such fragments in polynomial-time. We propose to use such fragments to answer queries about whether a given probability distribution satisfies a given system of constraints and bounds on expected values. We show that in answering such queries, such constraints and bounds can be implicitly learned from partial observations in polynomial-time as well. It is known that this logic is capable of deriving many bounds that are useful in probabilistic analysis. We show here that it furthermore captures useful polynomial-time fragments of resolution. Thus, these fragments are also quite expressive.

Conditional Sparse $\ell_p$-norm Regression With Optimal Probability

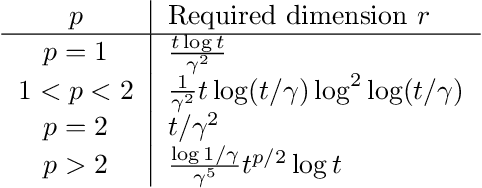
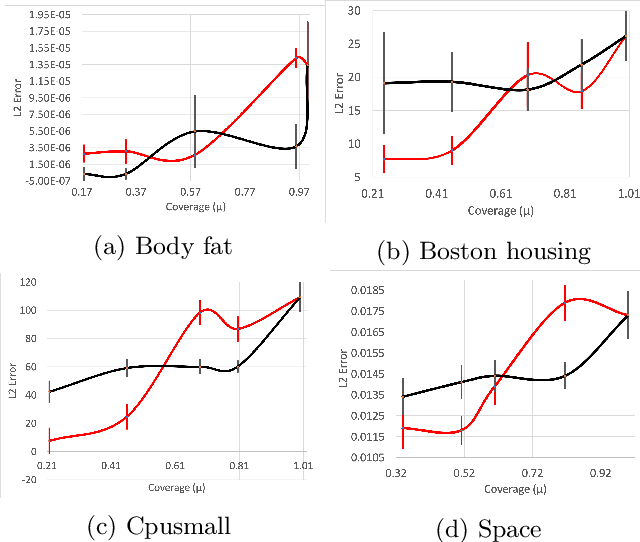
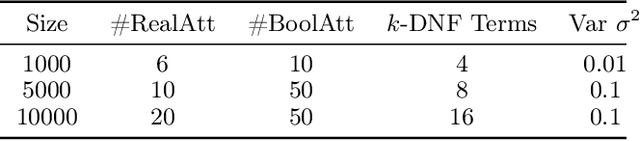
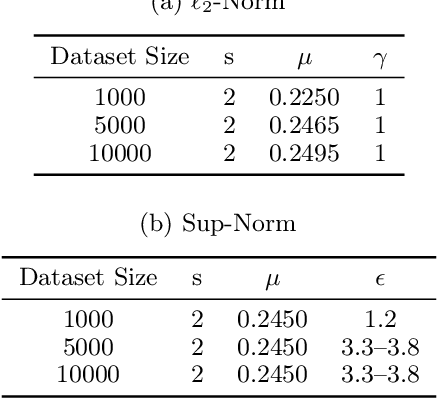
We consider the following conditional linear regression problem: the task is to identify both (i) a $k$-DNF condition $c$ and (ii) a linear rule $f$ such that the probability of $c$ is (approximately) at least some given bound $\mu$, and $f$ minimizes the $\ell_p$ loss of predicting the target $z$ in the distribution of examples conditioned on $c$. Thus, the task is to identify a portion of the distribution on which a linear rule can provide a good fit. Algorithms for this task are useful in cases where simple, learnable rules only accurately model portions of the distribution. The prior state-of-the-art for such algorithms could only guarantee finding a condition of probability $\Omega(\mu/n^k)$ when a condition of probability $\mu$ exists, and achieved an $O(n^k)$-approximation to the target loss, where $n$ is the number of Boolean attributes. Here, we give efficient algorithms for solving this task with a condition $c$ that nearly matches the probability of the ideal condition, while also improving the approximation to the target loss. We also give an algorithm for finding a $k$-DNF reference class for prediction at a given query point, that obtains a sparse regression fit that has loss within $O(n^k)$ of optimal among all sparse regression parameters and sufficiently large $k$-DNF reference classes containing the query point.