Safe Learning of Lifted Action Models

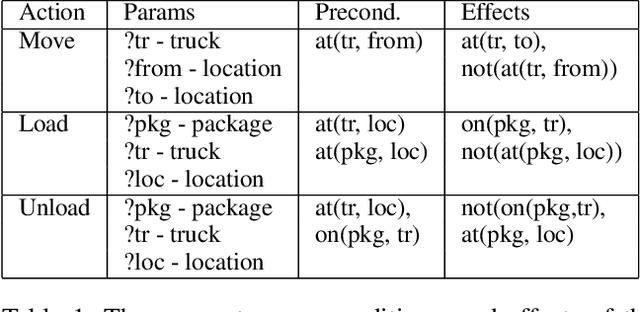
Creating a domain model, even for classical, domain-independent planning, is a notoriously hard knowledge-engineering task. A natural approach to solve this problem is to learn a domain model from observations. However, model learning approaches frequently do not provide safety guarantees: the learned model may assume actions are applicable when they are not, and may incorrectly capture actions' effects. This may result in generating plans that will fail when executed. In some domains such failures are not acceptable, due to the cost of failure or inability to replan online after failure. In such settings, all learning must be done offline, based on some observations collected, e.g., by some other agents or a human. Through this learning, the task is to generate a plan that is guaranteed to be successful. This is called the model-free planning problem. Prior work proposed an algorithm for solving the model-free planning problem in classical planning. However, they were limited to learning grounded domains, and thus they could not scale. We generalize this prior work and propose the first safe model-free planning algorithm for lifted domains. We prove the correctness of our approach, and provide a statistical analysis showing that the number of trajectories needed to solve future problems with high probability is linear in the potential size of the domain model. We also present experiments on twelve IPC domains showing that our approach is able to learn the real action model in all cases with at most two trajectories.

Conditional Sparse $\ell_p$-norm Regression With Optimal Probability

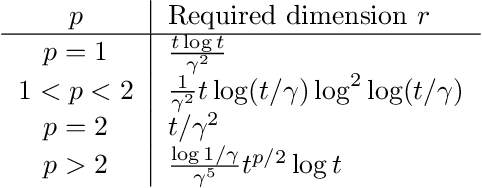
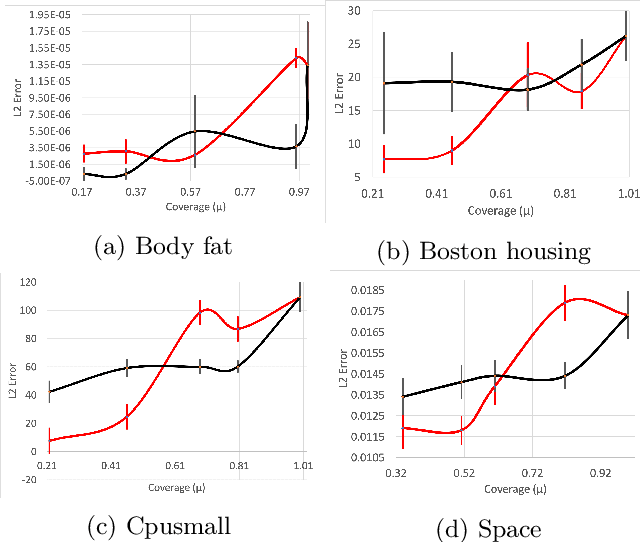
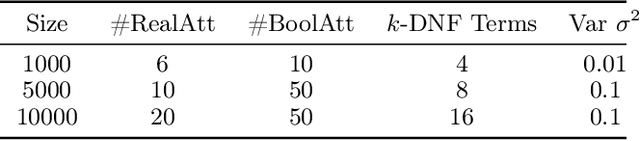
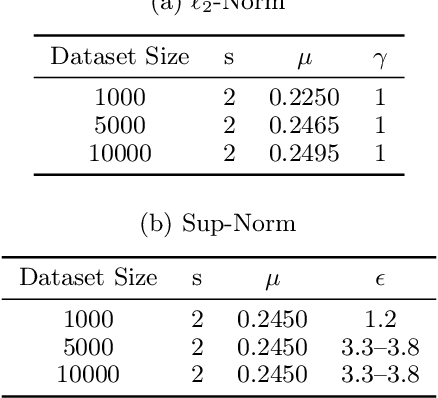
We consider the following conditional linear regression problem: the task is to identify both (i) a $k$-DNF condition $c$ and (ii) a linear rule $f$ such that the probability of $c$ is (approximately) at least some given bound $\mu$, and $f$ minimizes the $\ell_p$ loss of predicting the target $z$ in the distribution of examples conditioned on $c$. Thus, the task is to identify a portion of the distribution on which a linear rule can provide a good fit. Algorithms for this task are useful in cases where simple, learnable rules only accurately model portions of the distribution. The prior state-of-the-art for such algorithms could only guarantee finding a condition of probability $\Omega(\mu/n^k)$ when a condition of probability $\mu$ exists, and achieved an $O(n^k)$-approximation to the target loss, where $n$ is the number of Boolean attributes. Here, we give efficient algorithms for solving this task with a condition $c$ that nearly matches the probability of the ideal condition, while also improving the approximation to the target loss. We also give an algorithm for finding a $k$-DNF reference class for prediction at a given query point, that obtains a sparse regression fit that has loss within $O(n^k)$ of optimal among all sparse regression parameters and sufficiently large $k$-DNF reference classes containing the query point.