John Hainline
Conditional Sparse $\ell_p$-norm Regression With Optimal Probability
Jun 26, 2018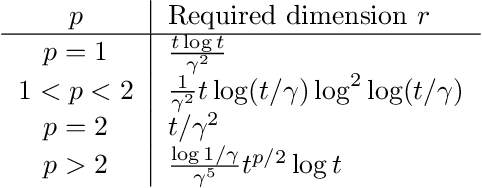
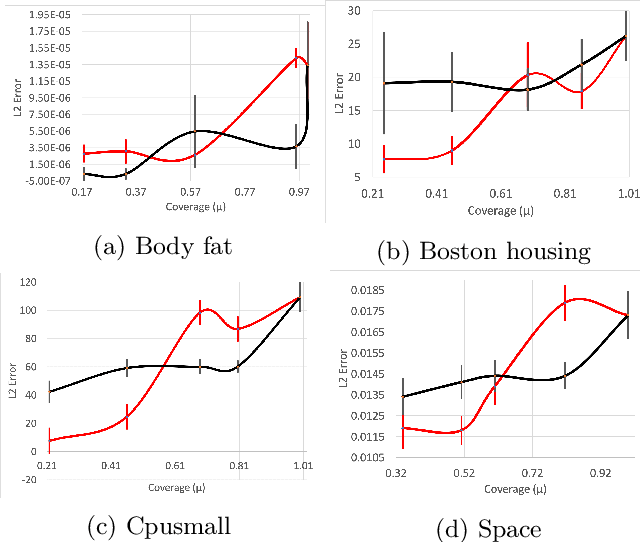
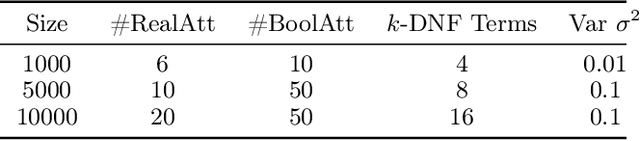
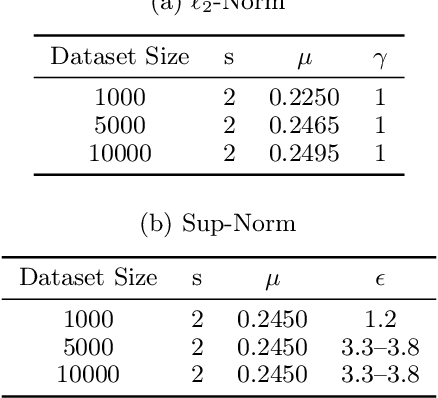
Abstract:We consider the following conditional linear regression problem: the task is to identify both (i) a $k$-DNF condition $c$ and (ii) a linear rule $f$ such that the probability of $c$ is (approximately) at least some given bound $\mu$, and $f$ minimizes the $\ell_p$ loss of predicting the target $z$ in the distribution of examples conditioned on $c$. Thus, the task is to identify a portion of the distribution on which a linear rule can provide a good fit. Algorithms for this task are useful in cases where simple, learnable rules only accurately model portions of the distribution. The prior state-of-the-art for such algorithms could only guarantee finding a condition of probability $\Omega(\mu/n^k)$ when a condition of probability $\mu$ exists, and achieved an $O(n^k)$-approximation to the target loss, where $n$ is the number of Boolean attributes. Here, we give efficient algorithms for solving this task with a condition $c$ that nearly matches the probability of the ideal condition, while also improving the approximation to the target loss. We also give an algorithm for finding a $k$-DNF reference class for prediction at a given query point, that obtains a sparse regression fit that has loss within $O(n^k)$ of optimal among all sparse regression parameters and sufficiently large $k$-DNF reference classes containing the query point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge