A fully automated urban PV parameterization framework for improved estimation of energy production profiles

Accurate parameterization of rooftop photovoltaic (PV) installations is critical for effective grid management and strategic large-scale solar deployment. The lack of high-fidelity datasets for PV configuration parameters often compels practitioners to rely on coarse assumptions, undermining both the temporal and numerical accuracy of large-scale PV performance modeling. This study introduces a fully automated framework that innovatively integrates remote sensing data, semantic segmentation, polygon-vector refinement, tilt-azimuth estimation, and module layout inference to produce a richly attributed GIS dataset of distributed PV. Applied to Eindhoven (the Netherlands), the method achieves a correlation ($R^2$) of 0.92 with Distribution System Operator (DSO) records, while capacity estimates for 73$\%$ of neighborhoods demonstrate agreement within a $\pm$25$\%$ margin of recorded data. Additionally, by accurately capturing actual system configuration parameters (e.g., tilt, azimuth, module layout) and seamlessly linking them to advanced performance models, the method yields more reliable PV energy generation forecasts within the distribution networks. Centering our experiments toward a high PV-penetration community, configuration-aware simulations help to reduce Mean Absolute Percentage Error (MAPE) of energy generation modeling by up to 160$\%$ compared to the conventional assumption-based approaches. Furthermore, owing to its modular design and reliance on readily available geospatial resources, the workflow can be extended across diverse regions, offering a scalable solution for robust urban solar integration.

Best Practices for Distilling Large Language Models into BERT for Web Search Ranking

Recent studies have highlighted the significant potential of Large Language Models (LLMs) as zero-shot relevance rankers. These methods predominantly utilize prompt learning to assess the relevance between queries and documents by generating a ranked list of potential documents. Despite their promise, the substantial costs associated with LLMs pose a significant challenge for their direct implementation in commercial search systems. To overcome this barrier and fully exploit the capabilities of LLMs for text ranking, we explore techniques to transfer the ranking expertise of LLMs to a more compact model similar to BERT, using a ranking loss to enable the deployment of less resource-intensive models. Specifically, we enhance the training of LLMs through Continued Pre-Training, taking the query as input and the clicked title and summary as output. We then proceed with supervised fine-tuning of the LLM using a rank loss, assigning the final token as a representative of the entire sentence. Given the inherent characteristics of autoregressive language models, only the final token </s> can encapsulate all preceding tokens. Additionally, we introduce a hybrid point-wise and margin MSE loss to transfer the ranking knowledge from LLMs to smaller models like BERT. This method creates a viable solution for environments with strict resource constraints. Both offline and online evaluations have confirmed the efficacy of our approach, and our model has been successfully integrated into a commercial web search engine as of February 2024.

Wolf2Pack: The AutoFusion Framework for Dynamic Parameter Fusion

In the rapidly evolving field of deep learning, specialized models have driven significant advancements in tasks such as computer vision and natural language processing. However, this specialization leads to a fragmented ecosystem where models lack the adaptability for broader applications. To overcome this, we introduce AutoFusion, an innovative framework that fuses distinct model parameters(with the same architecture) for multi-task learning without pre-trained checkpoints. Using an unsupervised, end-to-end approach, AutoFusion dynamically permutes model parameters at each layer, optimizing the combination through a loss-minimization process that does not require labeled data. We validate AutoFusion's effectiveness through experiments on commonly used benchmark datasets, demonstrating superior performance over established methods like Weight Interpolation, Git Re-Basin, and ZipIt. Our framework offers a scalable and flexible solution for model integration, positioning it as a powerful tool for future research and practical applications.

PEPL: Precision-Enhanced Pseudo-Labeling for Fine-Grained Image Classification in Semi-Supervised Learning

Fine-grained image classification has witnessed significant advancements with the advent of deep learning and computer vision technologies. However, the scarcity of detailed annotations remains a major challenge, especially in scenarios where obtaining high-quality labeled data is costly or time-consuming. To address this limitation, we introduce Precision-Enhanced Pseudo-Labeling(PEPL) approach specifically designed for fine-grained image classification within a semi-supervised learning framework. Our method leverages the abundance of unlabeled data by generating high-quality pseudo-labels that are progressively refined through two key phases: initial pseudo-label generation and semantic-mixed pseudo-label generation. These phases utilize Class Activation Maps (CAMs) to accurately estimate the semantic content and generate refined labels that capture the essential details necessary for fine-grained classification. By focusing on semantic-level information, our approach effectively addresses the limitations of standard data augmentation and image-mixing techniques in preserving critical fine-grained features. We achieve state-of-the-art performance on benchmark datasets, demonstrating significant improvements over existing semi-supervised strategies, with notable boosts in accuracy and robustness.Our code has been open sourced at https://github.com/TianSuya/SemiFG.

QUITO-X: An Information Bottleneck-based Compression Algorithm with Cross-Attention

Generative LLM have achieved significant success in various industrial tasks and can effectively adapt to vertical domains and downstream tasks through ICL. However, with tasks becoming increasingly complex, the context length required by ICL is also getting longer, and two significant issues arise: (i) The excessively long context leads to high costs and inference delays. (ii) A substantial amount of task-irrelevant information introduced by long contexts exacerbates the "lost in the middle" problem. Recently, compressing prompts by removing tokens according to some metric obtained from some causal language models, such as llama-7b, has emerged as an effective approach to mitigate these issues. However, the metric used by prior method such as self-information or PPL do not fully align with the objective of distinuishing the most important tokens when conditioning on query. In this work, we introduce information bottleneck theory to carefully examine the properties required by the metric. Inspired by this, we use cross-attention in encoder-decoder architecture as a new metric. Our simple method leads to significantly better performance in smaller models with lower latency. We evaluate our method on four datasets: DROP, CoQA, SQuAD, and Quoref. The experimental results show that, while maintaining the same performance, our compression rate can improve by nearly 25% over previous SOTA. Remarkably, in experiments where 25% of the tokens are removed, our model's EM score for answers sometimes even exceeds that of the control group using uncompressed text as context.

Leveraging Contaminated Datasets to Learn Clean-Data Distribution with Purified Generative Adversarial Networks

Generative adversarial networks (GANs) are known for their strong abilities on capturing the underlying distribution of training instances. Since the seminal work of GAN, many variants of GAN have been proposed. However, existing GANs are almost established on the assumption that the training dataset is clean. But in many real-world applications, this may not hold, that is, the training dataset may be contaminated by a proportion of undesired instances. When training on such datasets, existing GANs will learn a mixture distribution of desired and contaminated instances, rather than the desired distribution of desired data only (target distribution). To learn the target distribution from contaminated datasets, two purified generative adversarial networks (PuriGAN) are developed, in which the discriminators are augmented with the capability to distinguish between target and contaminated instances by leveraging an extra dataset solely composed of contamination instances. We prove that under some mild conditions, the proposed PuriGANs are guaranteed to converge to the distribution of desired instances. Experimental results on several datasets demonstrate that the proposed PuriGANs are able to generate much better images from the desired distribution than comparable baselines when trained on contaminated datasets. In addition, we also demonstrate the usefulness of PuriGAN on downstream applications by applying it to the tasks of semi-supervised anomaly detection on contaminated datasets and PU-learning. Experimental results show that PuriGAN is able to deliver the best performance over comparable baselines on both tasks.

Anomaly Detection by Leveraging Incomplete Anomalous Knowledge with Anomaly-Aware Bidirectional GANs

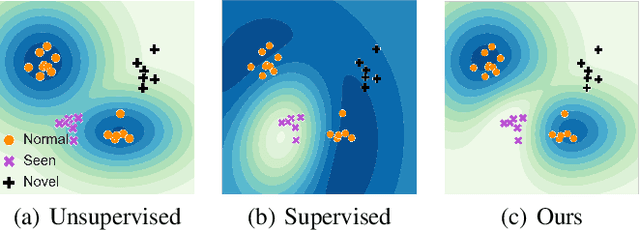
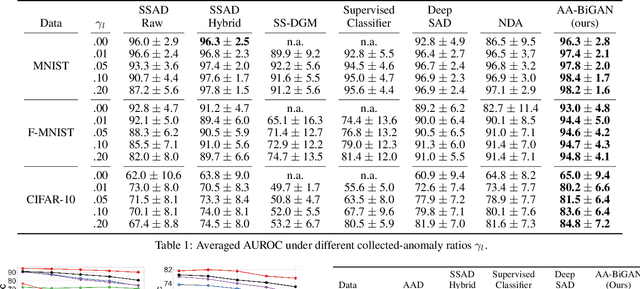
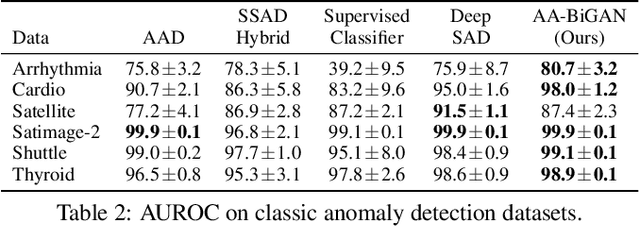
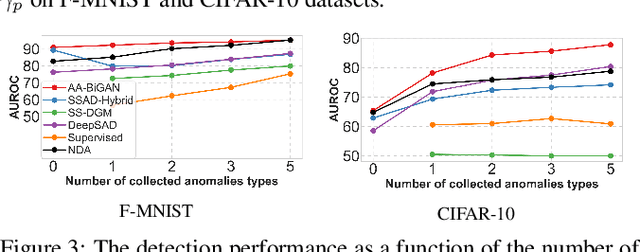
The goal of anomaly detection is to identify anomalous samples from normal ones. In this paper, a small number of anomalies are assumed to be available at the training stage, but they are assumed to be collected only from several anomaly types, leaving the majority of anomaly types not represented in the collected anomaly dataset at all. To effectively leverage this kind of incomplete anomalous knowledge represented by the collected anomalies, we propose to learn a probability distribution that can not only model the normal samples, but also guarantee to assign low density values for the collected anomalies. To this end, an anomaly-aware generative adversarial network (GAN) is developed, which, in addition to modeling the normal samples as most GANs do, is able to explicitly avoid assigning probabilities for collected anomalous samples. Moreover, to facilitate the computation of anomaly detection criteria like reconstruction error, the proposed anomaly-aware GAN is designed to be bidirectional, attaching an encoder for the generator. Extensive experimental results demonstrate that our proposed method is able to effectively make use of the incomplete anomalous information, leading to significant performance gains compared to existing methods.

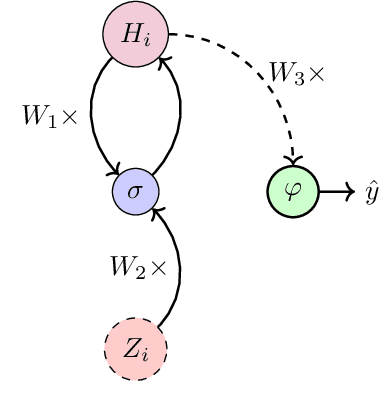
Global Convergence and Stability of Stochastic Gradient Descent

In machine learning, stochastic gradient descent (SGD) is widely deployed to train models using highly non-convex objectives with equally complex noise models. Unfortunately, SGD theory often makes restrictive assumptions that fail to capture the non-convexity of real problems, and almost entirely ignore the complex noise models that exist in practice. In this work, we make substantial progress on this shortcoming. First, we establish that SGD's iterates will either globally converge to a stationary point or diverge under nearly arbitrary nonconvexity and noise models. Under a slightly more restrictive assumption on the joint behavior of the non-convexity and noise model that generalizes current assumptions in the literature, we show that the objective function cannot diverge, even if the iterates diverge. As a consequence of our results, SGD can be applied to a greater range of stochastic optimization problems with confidence about its global convergence behavior and stability.