KeystoneML: Optimizing Pipelines for Large-Scale Advanced Analytics

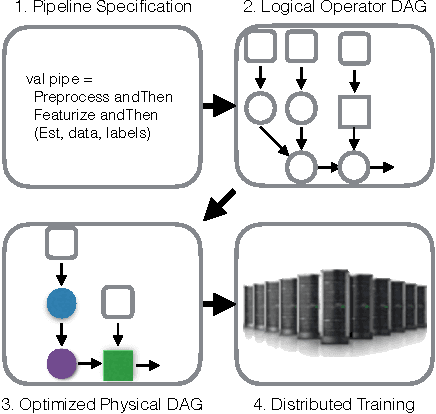
Modern advanced analytics applications make use of machine learning techniques and contain multiple steps of domain-specific and general-purpose processing with high resource requirements. We present KeystoneML, a system that captures and optimizes the end-to-end large-scale machine learning applications for high-throughput training in a distributed environment with a high-level API. This approach offers increased ease of use and higher performance over existing systems for large scale learning. We demonstrate the effectiveness of KeystoneML in achieving high quality statistical accuracy and scalable training using real world datasets in several domains. By optimizing execution KeystoneML achieves up to 15x training throughput over unoptimized execution on a real image classification application.

Gradient Descent Learns Linear Dynamical Systems

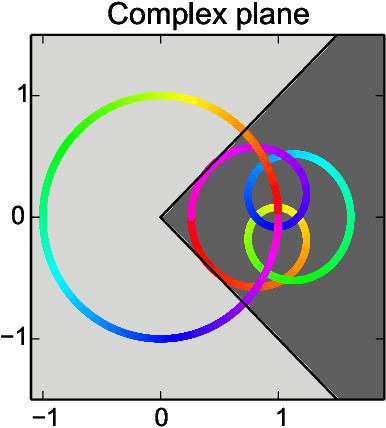
We prove that gradient descent efficiently converges to the global optimizer of the maximum likelihood objective of an unknown linear time-invariant dynamical system from a sequence of noisy observations generated by the system. Even though the objective function is non-convex, we provide polynomial running time and sample complexity bounds under strong but natural assumptions. Linear systems identification has been studied for many decades, yet, to the best of our knowledge, these are the first polynomial guarantees for the problem we consider.

CYCLADES: Conflict-free Asynchronous Machine Learning

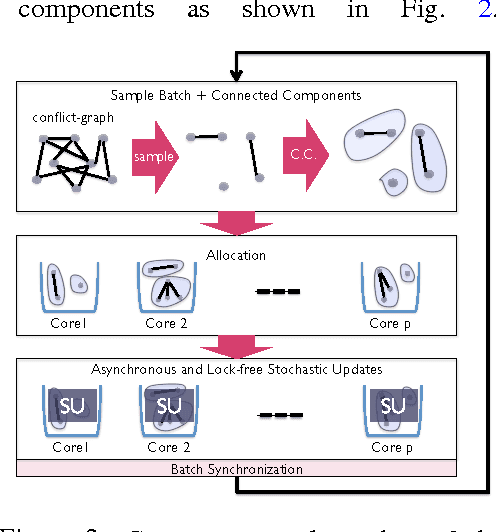
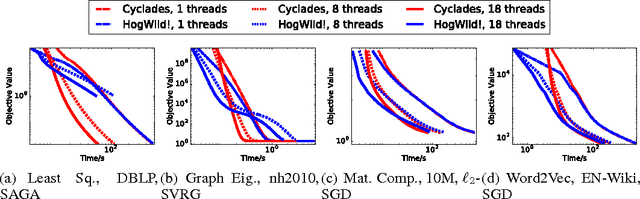
We present CYCLADES, a general framework for parallelizing stochastic optimization algorithms in a shared memory setting. CYCLADES is asynchronous during shared model updates, and requires no memory locking mechanisms, similar to HOGWILD!-type algorithms. Unlike HOGWILD!, CYCLADES introduces no conflicts during the parallel execution, and offers a black-box analysis for provable speedups across a large family of algorithms. Due to its inherent conflict-free nature and cache locality, our multi-core implementation of CYCLADES consistently outperforms HOGWILD!-type algorithms on sufficiently sparse datasets, leading to up to 40% speedup gains compared to the HOGWILD! implementation of SGD, and up to 5x gains over asynchronous implementations of variance reduction algorithms.

Perturbed Iterate Analysis for Asynchronous Stochastic Optimization

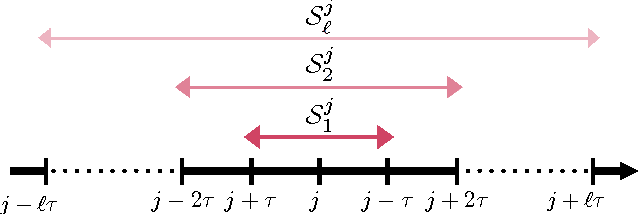
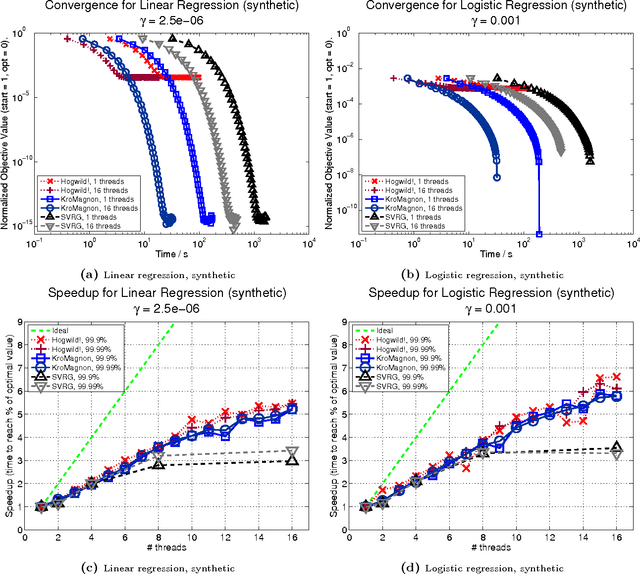
We introduce and analyze stochastic optimization methods where the input to each gradient update is perturbed by bounded noise. We show that this framework forms the basis of a unified approach to analyze asynchronous implementations of stochastic optimization algorithms.In this framework, asynchronous stochastic optimization algorithms can be thought of as serial methods operating on noisy inputs. Using our perturbed iterate framework, we provide new analyses of the Hogwild! algorithm and asynchronous stochastic coordinate descent, that are simpler than earlier analyses, remove many assumptions of previous models, and in some cases yield improved upper bounds on the convergence rates. We proceed to apply our framework to develop and analyze KroMagnon: a novel, parallel, sparse stochastic variance-reduced gradient (SVRG) algorithm. We demonstrate experimentally on a 16-core machine that the sparse and parallel version of SVRG is in some cases more than four orders of magnitude faster than the standard SVRG algorithm.

Best-of-K Bandits

This paper studies the Best-of-K Bandit game: At each time the player chooses a subset S among all N-choose-K possible options and observes reward max(X(i) : i in S) where X is a random vector drawn from a joint distribution. The objective is to identify the subset that achieves the highest expected reward with high probability using as few queries as possible. We present distribution-dependent lower bounds based on a particular construction which force a learner to consider all N-choose-K subsets, and match naive extensions of known upper bounds in the bandit setting obtained by treating each subset as a separate arm. Nevertheless, we present evidence that exhaustive search may be avoided for certain, favorable distributions because the influence of high-order order correlations may be dominated by lower order statistics. Finally, we present an algorithm and analysis for independent arms, which mitigates the surprising non-trivial information occlusion that occurs due to only observing the max in the subset. This may inform strategies for more general dependent measures, and we complement these result with independent-arm lower bounds.

Gradient Descent Converges to Minimizers

We show that gradient descent converges to a local minimizer, almost surely with random initialization. This is proved by applying the Stable Manifold Theorem from dynamical systems theory.

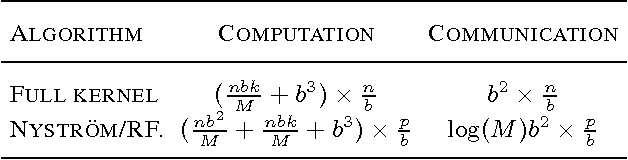
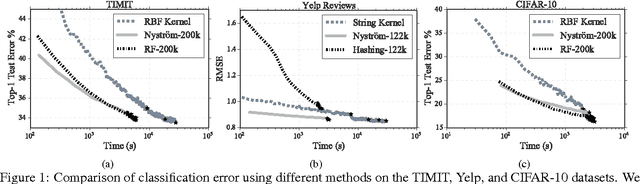
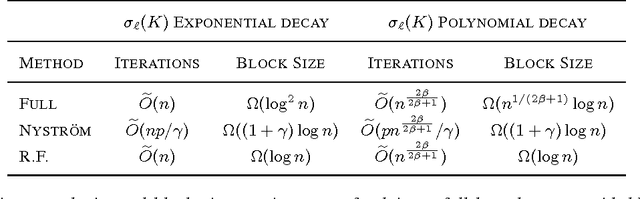
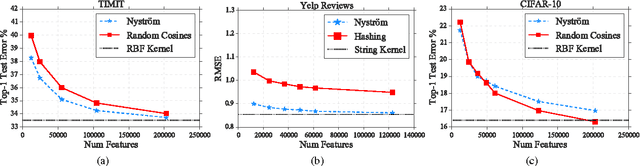
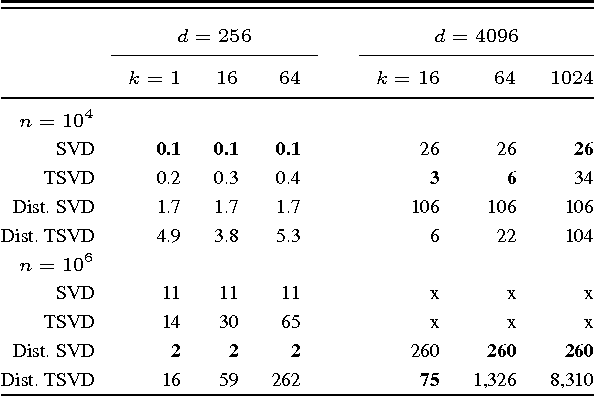
Large Scale Kernel Learning using Block Coordinate Descent

We demonstrate that distributed block coordinate descent can quickly solve kernel regression and classification problems with millions of data points. Armed with this capability, we conduct a thorough comparison between the full kernel, the Nystr\"om method, and random features on three large classification tasks from various domains. Our results suggest that the Nystr\"om method generally achieves better statistical accuracy than random features, but can require significantly more iterations of optimization. Lastly, we derive new rates for block coordinate descent which support our experimental findings when specialized to kernel methods.

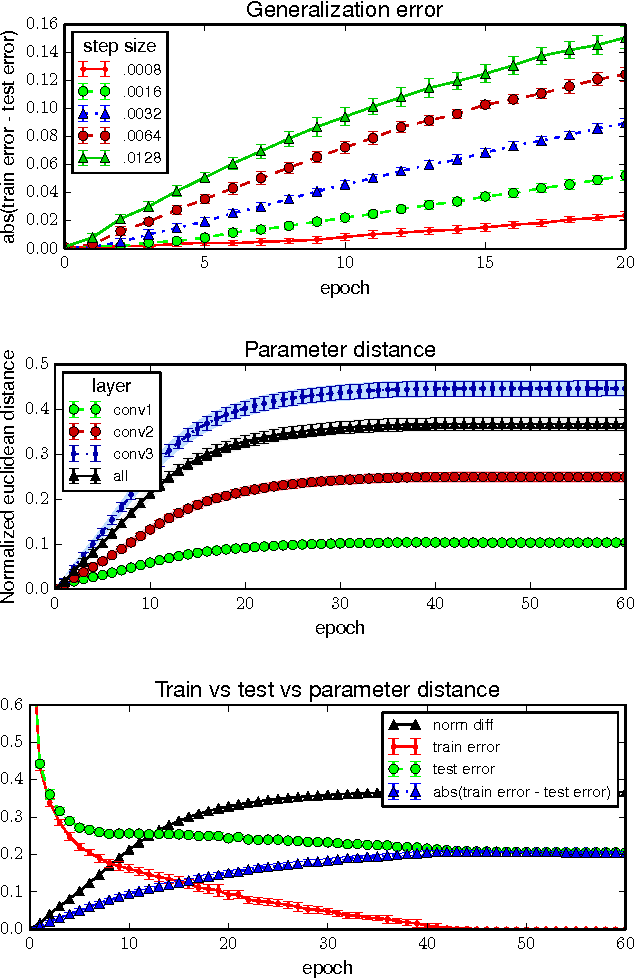
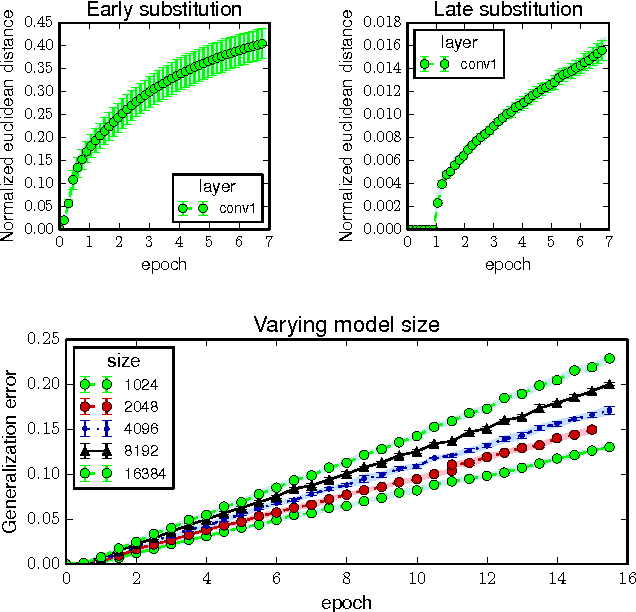
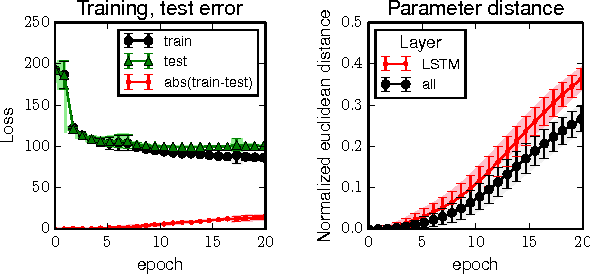
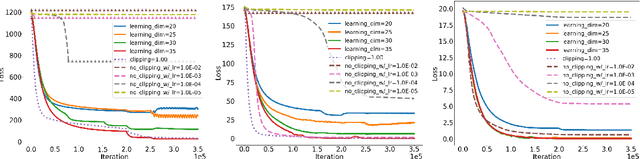
Train faster, generalize better: Stability of stochastic gradient descent

We show that parametric models trained by a stochastic gradient method (SGM) with few iterations have vanishing generalization error. We prove our results by arguing that SGM is algorithmically stable in the sense of Bousquet and Elisseeff. Our analysis only employs elementary tools from convex and continuous optimization. We derive stability bounds for both convex and non-convex optimization under standard Lipschitz and smoothness assumptions. Applying our results to the convex case, we provide new insights for why multiple epochs of stochastic gradient methods generalize well in practice. In the non-convex case, we give a new interpretation of common practices in neural networks, and formally show that popular techniques for training large deep models are indeed stability-promoting. Our findings conceptually underscore the importance of reducing training time beyond its obvious benefit.

Sharp Time--Data Tradeoffs for Linear Inverse Problems

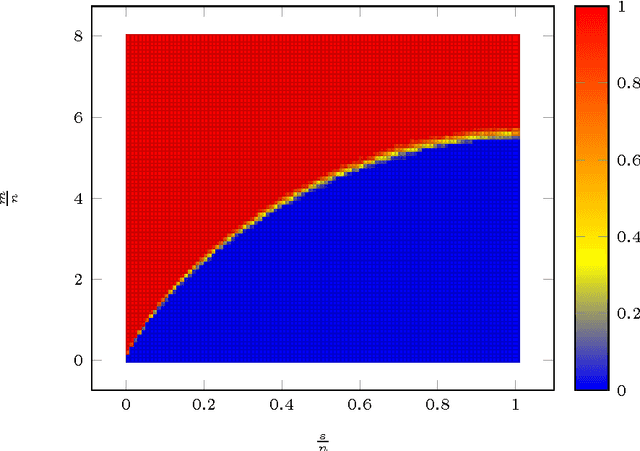
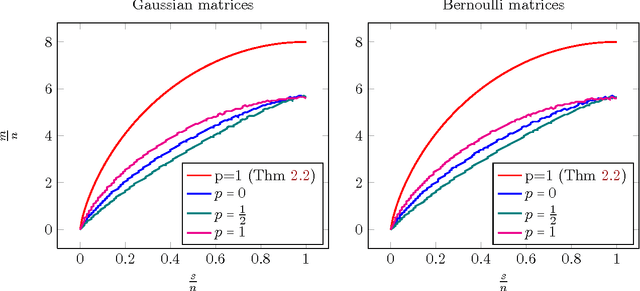
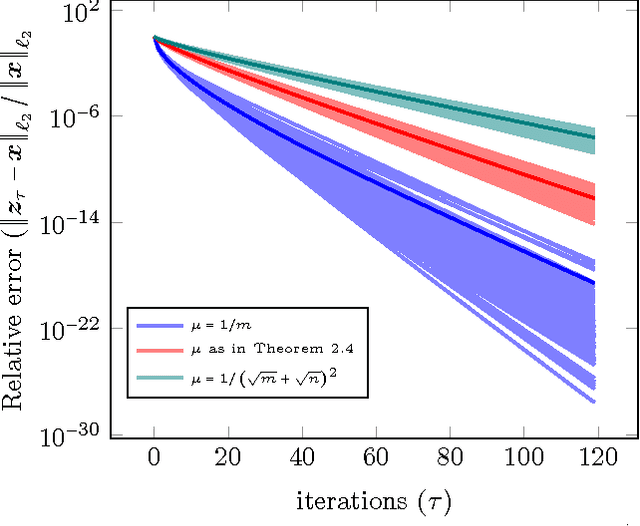
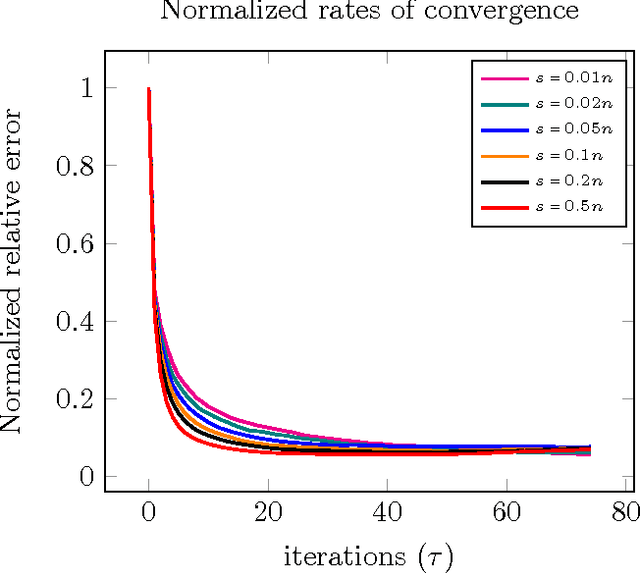
In this paper we characterize sharp time-data tradeoffs for optimization problems used for solving linear inverse problems. We focus on the minimization of a least-squares objective subject to a constraint defined as the sub-level set of a penalty function. We present a unified convergence analysis of the gradient projection algorithm applied to such problems. We sharply characterize the convergence rate associated with a wide variety of random measurement ensembles in terms of the number of measurements and structural complexity of the signal with respect to the chosen penalty function. The results apply to both convex and nonconvex constraints, demonstrating that a linear convergence rate is attainable even though the least squares objective is not strongly convex in these settings. When specialized to Gaussian measurements our results show that such linear convergence occurs when the number of measurements is merely 4 times the minimal number required to recover the desired signal at all (a.k.a. the phase transition). We also achieve a slower but geometric rate of convergence precisely above the phase transition point. Extensive numerical results suggest that the derived rates exactly match the empirical performance.

Isometric sketching of any set via the Restricted Isometry Property

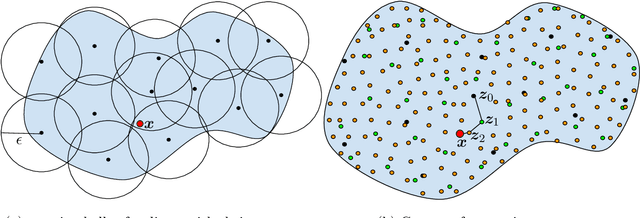
In this paper we show that for the purposes of dimensionality reduction certain class of structured random matrices behave similarly to random Gaussian matrices. This class includes several matrices for which matrix-vector multiply can be computed in log-linear time, providing efficient dimensionality reduction of general sets. In particular, we show that using such matrices any set from high dimensions can be embedded into lower dimensions with near optimal distortion. We obtain our results by connecting dimensionality reduction of any set to dimensionality reduction of sparse vectors via a chaining argument.