Benjamin Recht
Simple random search provides a competitive approach to reinforcement learning
Mar 19, 2018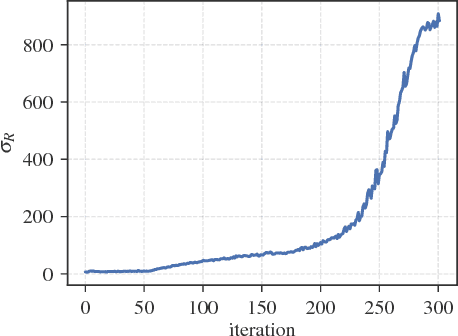
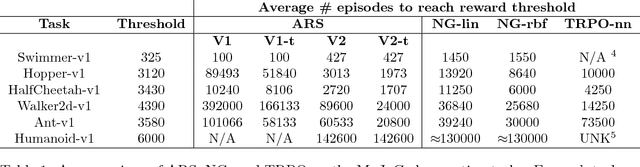
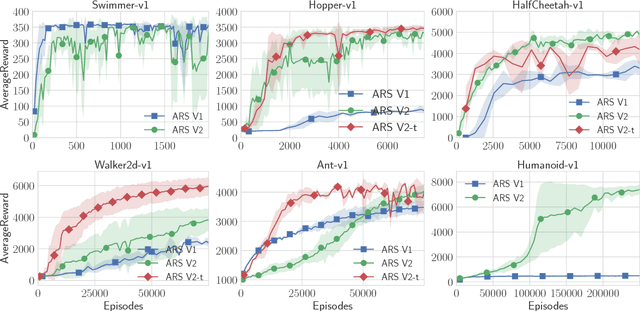
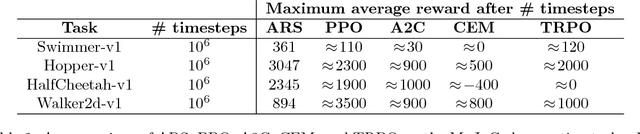
Abstract:A common belief in model-free reinforcement learning is that methods based on random search in the parameter space of policies exhibit significantly worse sample complexity than those that explore the space of actions. We dispel such beliefs by introducing a random search method for training static, linear policies for continuous control problems, matching state-of-the-art sample efficiency on the benchmark MuJoCo locomotion tasks. Our method also finds a nearly optimal controller for a challenging instance of the Linear Quadratic Regulator, a classical problem in control theory, when the dynamics are not known. Computationally, our random search algorithm is at least 15 times more efficient than the fastest competing model-free methods on these benchmarks. We take advantage of this computational efficiency to evaluate the performance of our method over hundreds of random seeds and many different hyperparameter configurations for each benchmark task. Our simulations highlight a high variability in performance in these benchmark tasks, suggesting that commonly used estimations of sample efficiency do not adequately evaluate the performance of RL algorithms.
On the Sample Complexity of the Linear Quadratic Regulator
Jan 25, 2018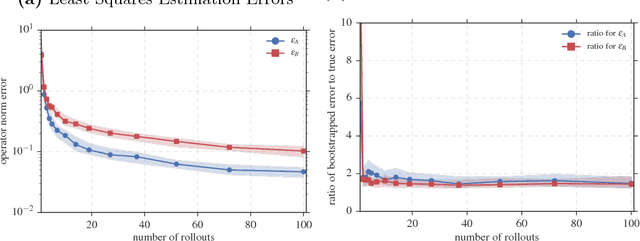
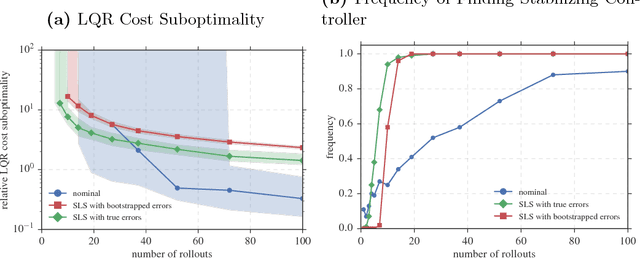
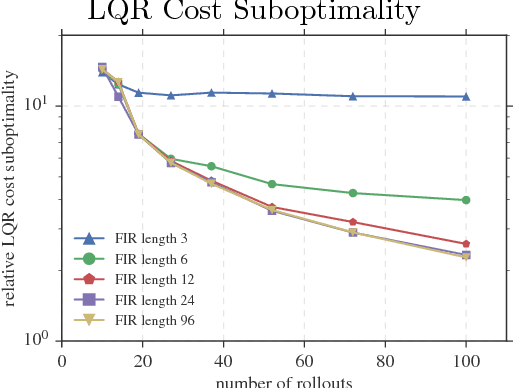
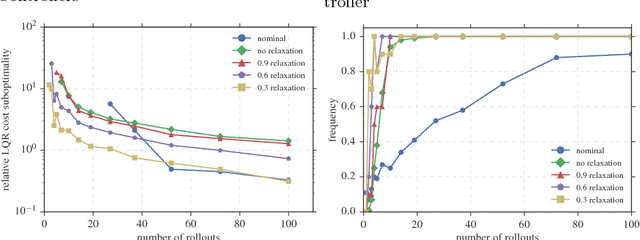
Abstract:This paper addresses the optimal control problem known as the Linear Quadratic Regulator in the case when the dynamics are unknown. We propose a multi-stage procedure, called Coarse-ID control, that estimates a model from a few experimental trials, estimates the error in that model with respect to the truth, and then designs a controller using both the model and uncertainty estimate. Our technique uses contemporary tools from random matrix theory to bound the error in the estimation procedure. We also employ a recently developed approach to control synthesis called System Level Synthesis that enables robust control design by solving a convex optimization problem. We provide end-to-end bounds on the relative error in control cost that are nearly optimal in the number of parameters and that highlight salient properties of the system to be controlled such as closed-loop sensitivity and optimal control magnitude. We show experimentally that the Coarse-ID approach enables efficient computation of a stabilizing controller in regimes where simple control schemes that do not take the model uncertainty into account fail to stabilize the true system.
Least-Squares Temporal Difference Learning for the Linear Quadratic Regulator
Dec 22, 2017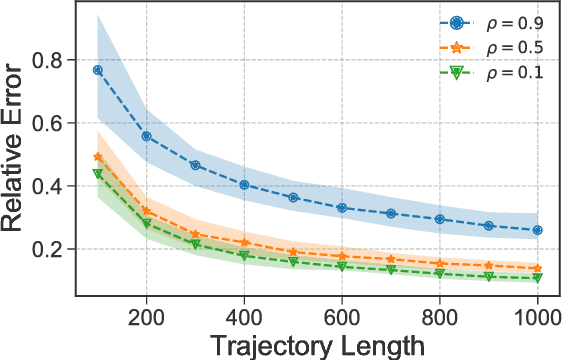
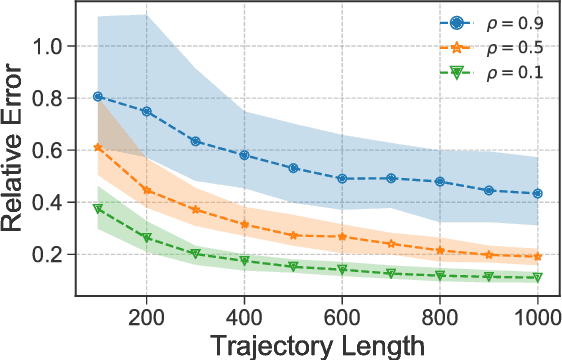
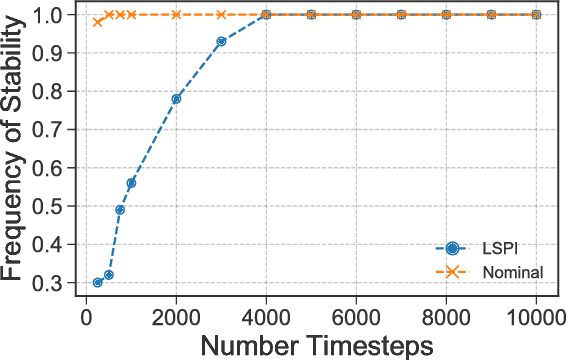
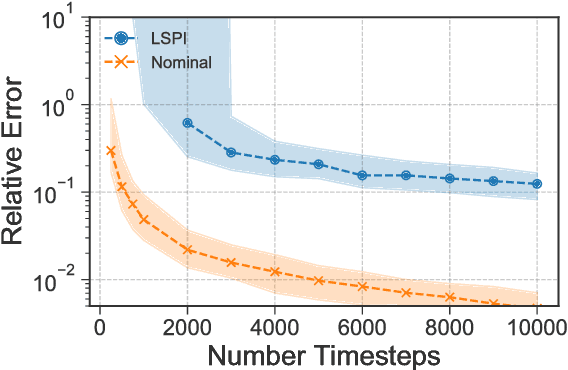
Abstract:Reinforcement learning (RL) has been successfully used to solve many continuous control tasks. Despite its impressive results however, fundamental questions regarding the sample complexity of RL on continuous problems remain open. We study the performance of RL in this setting by considering the behavior of the Least-Squares Temporal Difference (LSTD) estimator on the classic Linear Quadratic Regulator (LQR) problem from optimal control. We give the first finite-time analysis of the number of samples needed to estimate the value function for a fixed static state-feedback policy to within $\varepsilon$-relative error. In the process of deriving our result, we give a general characterization for when the minimum eigenvalue of the empirical covariance matrix formed along the sample path of a fast-mixing stochastic process concentrates above zero, extending a result by Koltchinskii and Mendelson in the independent covariates setting. Finally, we provide experimental evidence indicating that our analysis correctly captures the qualitative behavior of LSTD on several LQR instances.
Saturating Splines and Feature Selection
Dec 04, 2017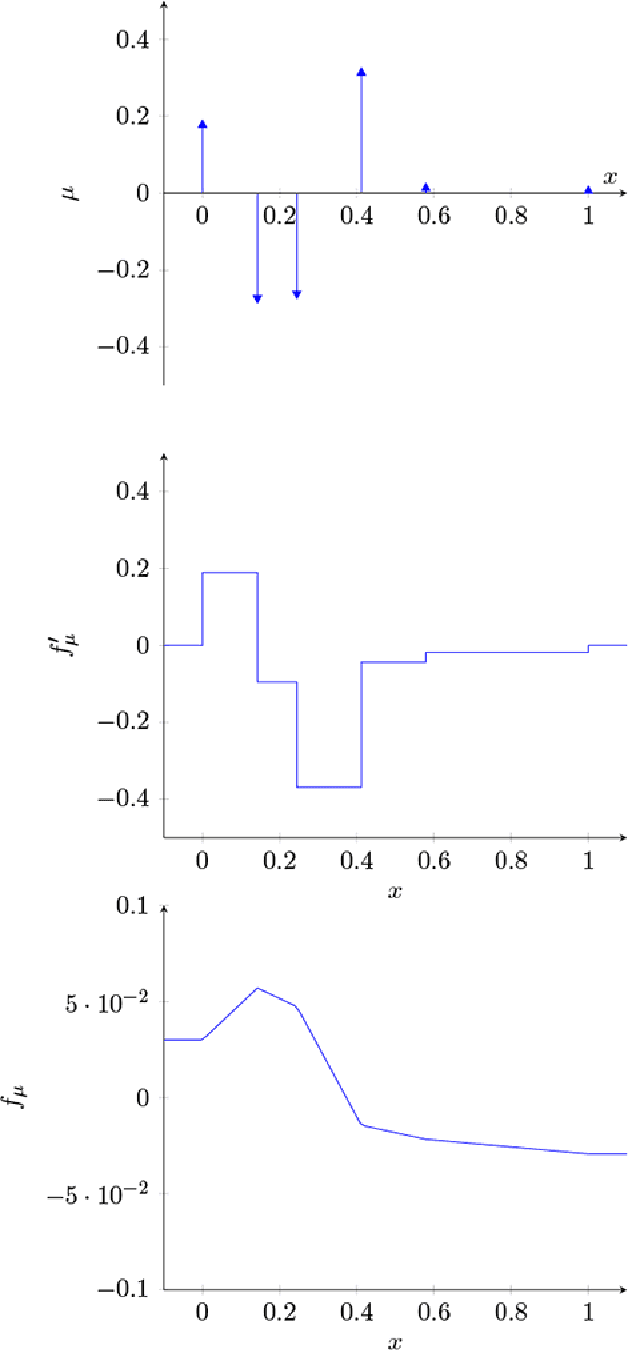
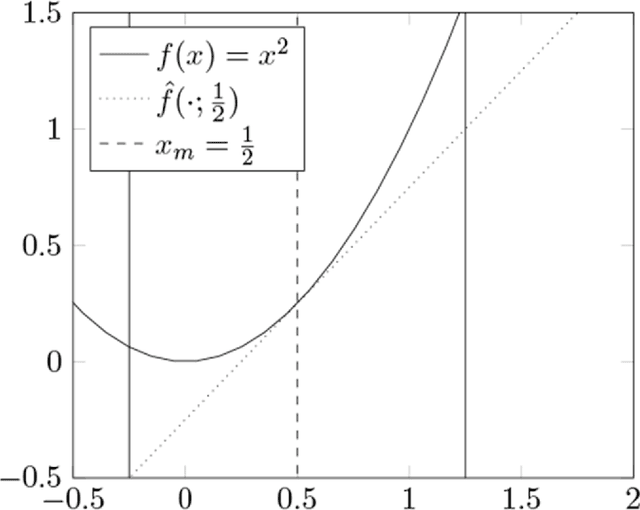
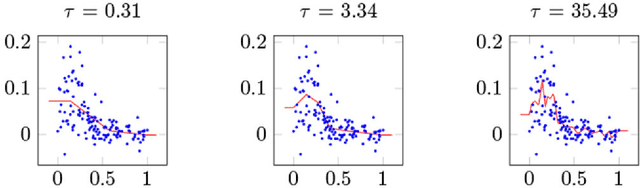
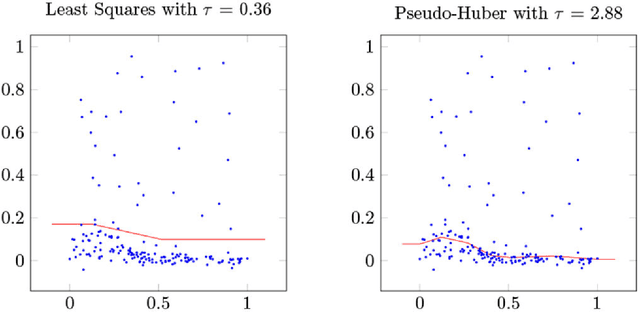
Abstract:We extend the adaptive regression spline model by incorporating saturation, the natural requirement that a function extend as a constant outside a certain range. We fit saturating splines to data using a convex optimization problem over a space of measures, which we solve using an efficient algorithm based on the conditional gradient method. Unlike many existing approaches, our algorithm solves the original infinite-dimensional (for splines of degree at least two) optimization problem without pre-specified knot locations. We then adapt our algorithm to fit generalized additive models with saturating splines as coordinate functions and show that the saturation requirement allows our model to simultaneously perform feature selection and nonlinear function fitting. Finally, we briefly sketch how the method can be extended to higher order splines and to different requirements on the extension outside the data range.
Non-Asymptotic Analysis of Robust Control from Coarse-Grained Identification
Nov 30, 2017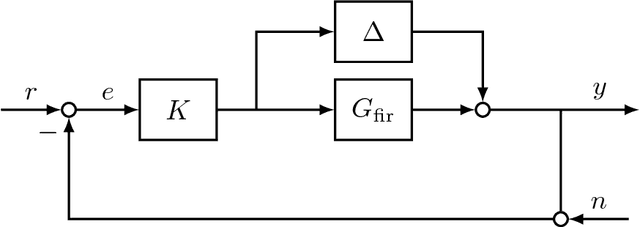
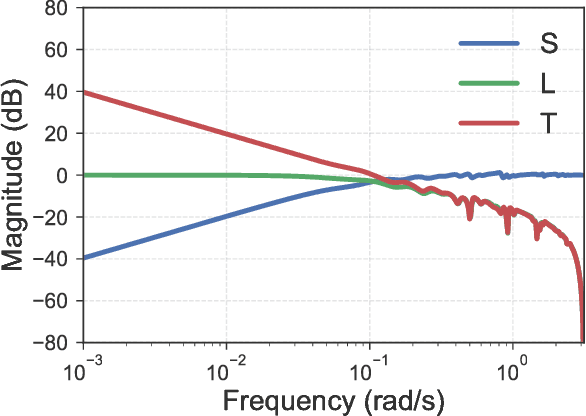
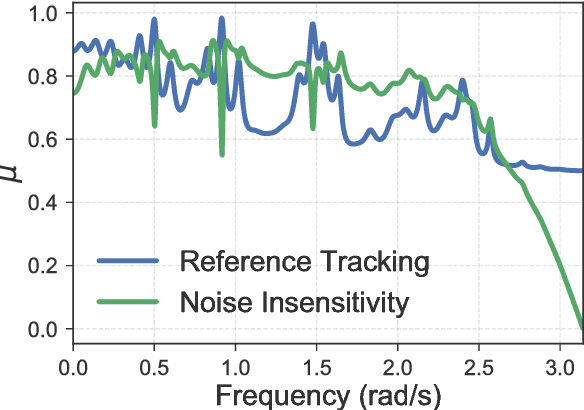
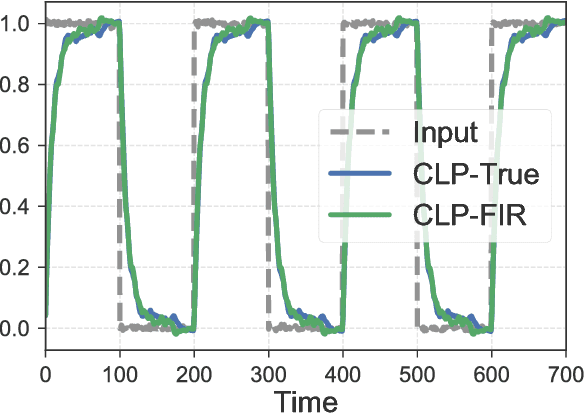
Abstract:This work explores the trade-off between the number of samples required to accurately build models of dynamical systems and the degradation of performance in various control objectives due to a coarse approximation. In particular, we show that simple models can be easily fit from input/output data and are sufficient for achieving various control objectives. We derive bounds on the number of noisy input/output samples from a stable linear time-invariant system that are sufficient to guarantee that the corresponding finite impulse response approximation is close to the true system in the $\mathcal{H}_\infty$-norm. We demonstrate that these demands are lower than those derived in prior art which aimed to accurately identify dynamical models. We also explore how different physical input constraints, such as power constraints, affect the sample complexity. Finally, we show how our analysis fits within the established framework of robust control, by demonstrating how a controller designed for an approximate system provably meets performance objectives on the true system.
First-order Methods Almost Always Avoid Saddle Points
Oct 20, 2017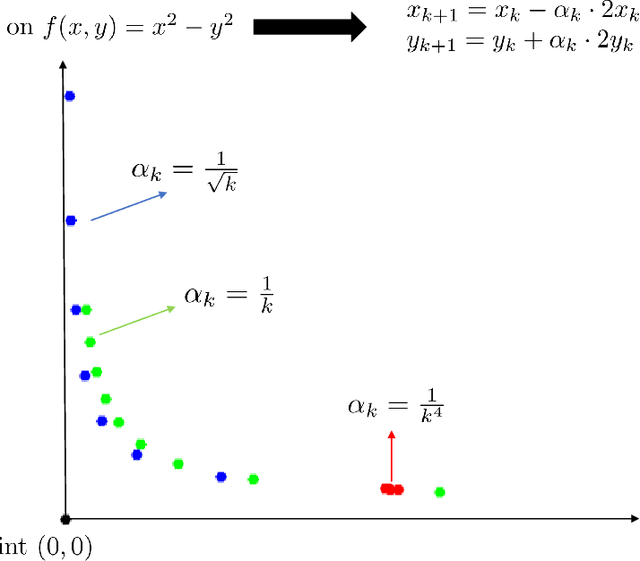
Abstract:We establish that first-order methods avoid saddle points for almost all initializations. Our results apply to a wide variety of first-order methods, including gradient descent, block coordinate descent, mirror descent and variants thereof. The connecting thread is that such algorithms can be studied from a dynamical systems perspective in which appropriate instantiations of the Stable Manifold Theorem allow for a global stability analysis. Thus, neither access to second-order derivative information nor randomness beyond initialization is necessary to provably avoid saddle points.
Flare Prediction Using Photospheric and Coronal Image Data
Aug 03, 2017
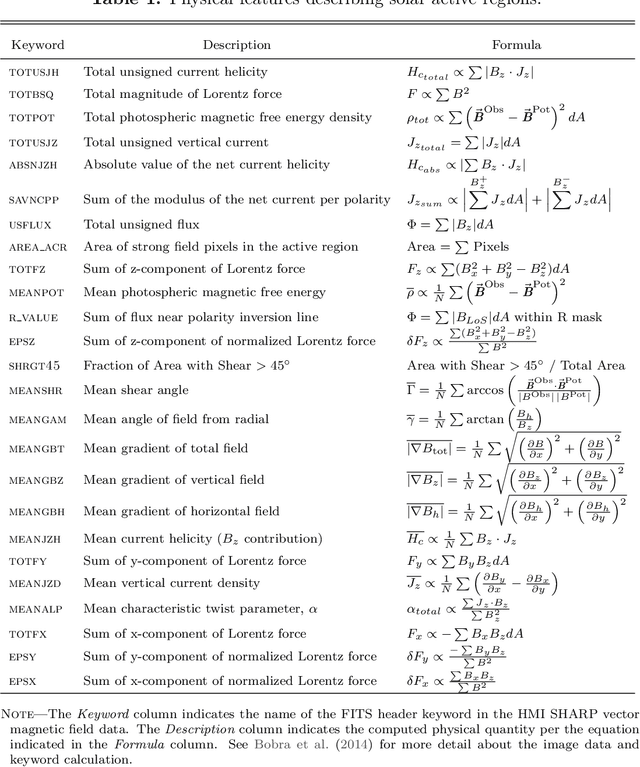
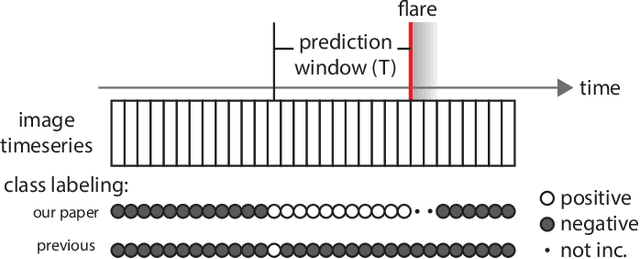

Abstract:The precise physical process that triggers solar flares is not currently understood. Here we attempt to capture the signature of this mechanism in solar image data of various wavelengths and use these signatures to predict flaring activity. We do this by developing an algorithm that [1] automatically generates features in 5.5 TB of image data taken by the Solar Dynamics Observatory of the solar photosphere, chromosphere, transition region, and corona during the time period between May 2010 and May 2014, [2] combines these features with other features based on flaring history and a physical understanding of putative flaring processes, and [3] classifies these features to predict whether a solar active region will flare within a time period of $T$ hours, where $T$ = 2 and 24. We find that when optimizing for the True Skill Score (TSS), photospheric vector magnetic field data combined with flaring history yields the best performance, and when optimizing for the area under the precision-recall curve, all the data are helpful. Our model performance yields a TSS of $0.84 \pm 0.03$ and $0.81 \pm 0.03$ in the $T$ = 2 and 24 hour cases, respectively, and a value of $0.13 \pm 0.07$ and $0.43 \pm 0.08$ for the area under the precision-recall curve in the $T$ = 2 and 24 hour cases, respectively. These relatively high scores are similar to, but not greater than, other attempts to predict solar flares. Given the similar values of algorithm performance across various types of models reported in the literature, we conclude that we can expect a certain baseline predictive capacity using these data. This is the first attempt to predict solar flares using photospheric vector magnetic field data as well as multiple wavelengths of image data from the chromosphere, transition region, and corona.
On kernel methods for covariates that are rankings
Jul 20, 2017Abstract:Permutation-valued features arise in a variety of applications, either in a direct way when preferences are elicited over a collection of items, or an indirect way in which numerical ratings are converted to a ranking. To date, there has been relatively limited study of regression, classification, and testing problems based on permutation-valued features, as opposed to permutation-valued responses. This paper studies the use of reproducing kernel Hilbert space methods for learning from permutation-valued features. These methods embed the rankings into an implicitly defined function space, and allow for efficient estimation of regression and test functions in this richer space. Our first contribution is to characterize both the feature spaces and spectral properties associated with two kernels for rankings, the Kendall and Mallows kernels. Using tools from representation theory, we explain the limited expressive power of the Kendall kernel by characterizing its degenerate spectrum, and in sharp contrast, we prove that Mallows' kernel is universal and characteristic. We also introduce families of polynomial kernels that interpolate between the Kendall (degree one) and Mallows' (infinite degree) kernels. We show the practical effectiveness of our methods via applications to Eurobarometer survey data as well as a Movielens ratings dataset.
Understanding deep learning requires rethinking generalization
Feb 26, 2017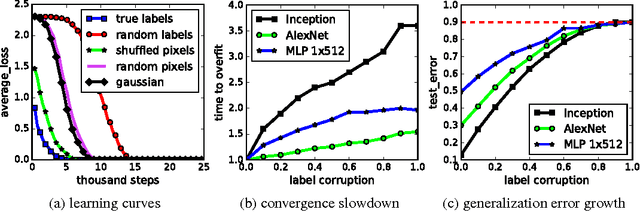
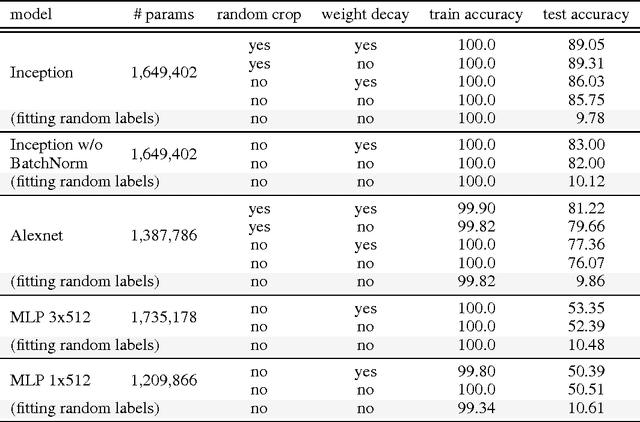
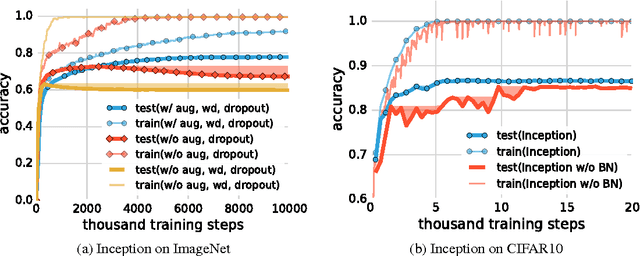
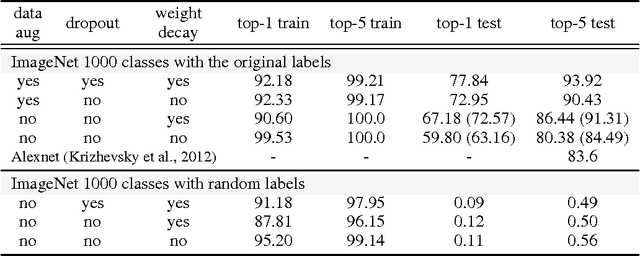
Abstract:Despite their massive size, successful deep artificial neural networks can exhibit a remarkably small difference between training and test performance. Conventional wisdom attributes small generalization error either to properties of the model family, or to the regularization techniques used during training. Through extensive systematic experiments, we show how these traditional approaches fail to explain why large neural networks generalize well in practice. Specifically, our experiments establish that state-of-the-art convolutional networks for image classification trained with stochastic gradient methods easily fit a random labeling of the training data. This phenomenon is qualitatively unaffected by explicit regularization, and occurs even if we replace the true images by completely unstructured random noise. We corroborate these experimental findings with a theoretical construction showing that simple depth two neural networks already have perfect finite sample expressivity as soon as the number of parameters exceeds the number of data points as it usually does in practice. We interpret our experimental findings by comparison with traditional models.
The Simulator: Understanding Adaptive Sampling in the Moderate-Confidence Regime
Feb 16, 2017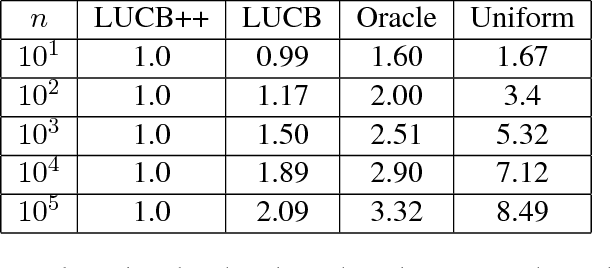
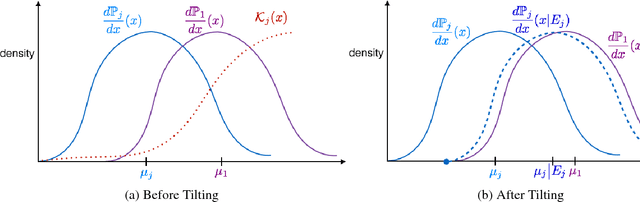
Abstract:We propose a novel technique for analyzing adaptive sampling called the {\em Simulator}. Our approach differs from the existing methods by considering not how much information could be gathered by any fixed sampling strategy, but how difficult it is to distinguish a good sampling strategy from a bad one given the limited amount of data collected up to any given time. This change of perspective allows us to match the strength of both Fano and change-of-measure techniques, without succumbing to the limitations of either method. For concreteness, we apply our techniques to a structured multi-arm bandit problem in the fixed-confidence pure exploration setting, where we show that the constraints on the means imply a substantial gap between the moderate-confidence sample complexity, and the asymptotic sample complexity as $\delta \to 0$ found in the literature. We also prove the first instance-based lower bounds for the top-k problem which incorporate the appropriate log-factors. Moreover, our lower bounds zero-in on the number of times each \emph{individual} arm needs to be pulled, uncovering new phenomena which are drowned out in the aggregate sample complexity. Our new analysis inspires a simple and near-optimal algorithm for the best-arm and top-k identification, the first {\em practical} algorithm of its kind for the latter problem which removes extraneous log factors, and outperforms the state-of-the-art in experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge