Label Information Enhanced Fraud Detection against Low Homophily in Graphs

Node classification is a substantial problem in graph-based fraud detection. Many existing works adopt Graph Neural Networks (GNNs) to enhance fraud detectors. While promising, currently most GNN-based fraud detectors fail to generalize to the low homophily setting. Besides, label utilization has been proved to be significant factor for node classification problem. But we find they are less effective in fraud detection tasks due to the low homophily in graphs. In this work, we propose GAGA, a novel Group AGgregation enhanced TrAnsformer, to tackle the above challenges. Specifically, the group aggregation provides a portable method to cope with the low homophily issue. Such an aggregation explicitly integrates the label information to generate distinguishable neighborhood information. Along with group aggregation, an attempt towards end-to-end trainable group encoding is proposed which augments the original feature space with the class labels. Meanwhile, we devise two additional learnable encodings to recognize the structural and relational context. Then, we combine the group aggregation and the learnable encodings into a Transformer encoder to capture the semantic information. Experimental results clearly show that GAGA outperforms other competitive graph-based fraud detectors by up to 24.39% on two trending public datasets and a real-world industrial dataset from Anonymous. Even more, the group aggregation is demonstrated to outperform other label utilization methods (e.g., C&S, BoT/UniMP) in the low homophily setting.

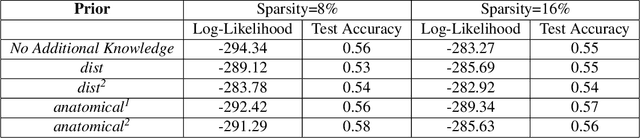
Differential Network Learning Beyond Data Samples

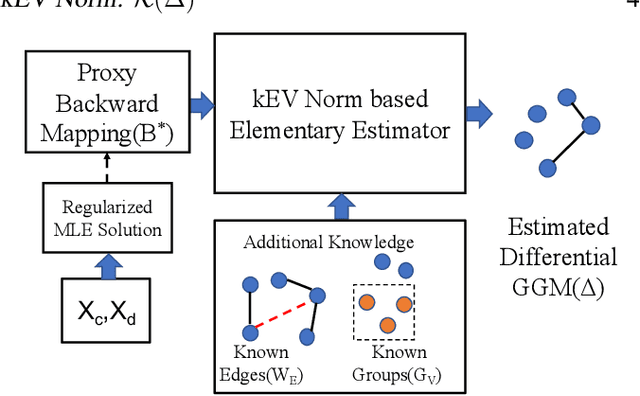
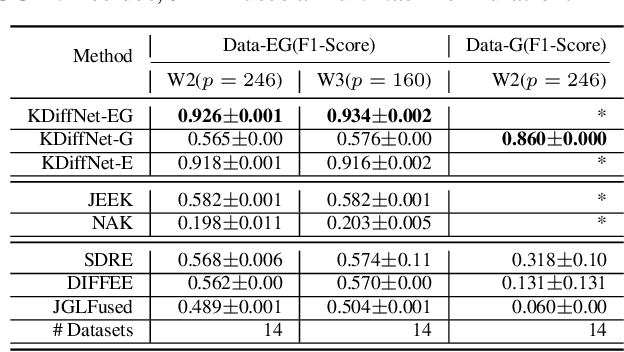
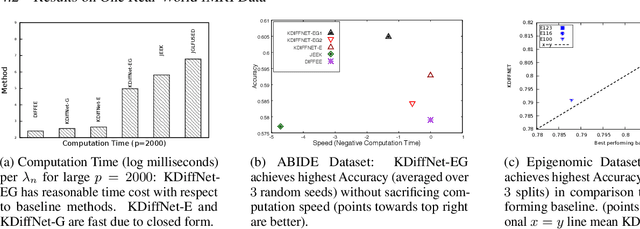
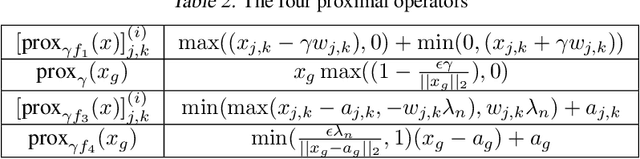
Learning the change of statistical dependencies between random variables is an essential task for many real-life applications, mostly in the high dimensional low sample regime. In this paper, we propose a novel differential parameter estimator that, in comparison to current methods, simultaneously allows (a) the flexible integration of multiple sources of information (data samples, variable groupings, extra pairwise evidence, etc.), (b) being scalable to a large number of variables, and (c) achieving a sharp asymptotic convergence rate. Our experiments, on more than 100 simulated and two real-world datasets, validate the flexibility of our approach and highlight the benefits of integrating spatial and anatomic information for brain connectome change discovery and epigenetic network identification.

Fast and Scalable Estimator for Sparse and Unit-Rank Higher-Order Regression Models

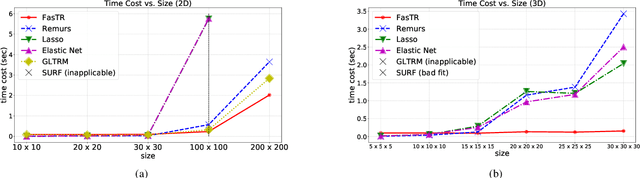
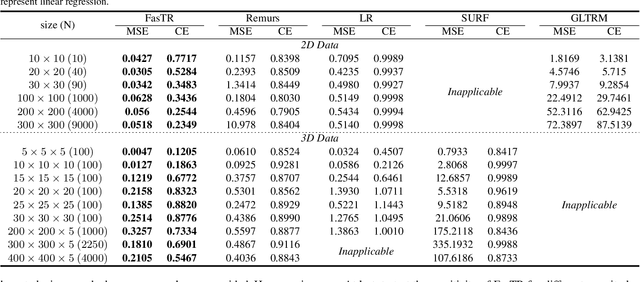
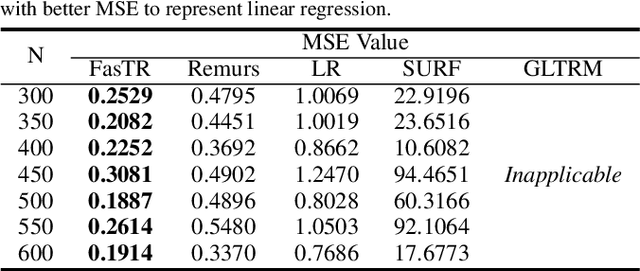
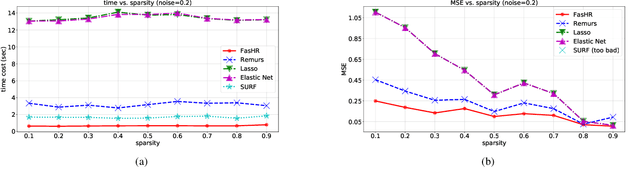
Because tensor data appear more and more frequently in various scientific researches and real-world applications, analyzing the relationship between tensor features and the univariate outcome becomes an elementary task in many fields. To solve this task, we propose \underline{Fa}st \underline{S}parse \underline{T}ensor \underline{R}egression model (FasTR) based on so-called unit-rank CANDECOMP/PARAFAC decomposition. FasTR first decomposes the tensor coefficient into component vectors and then estimates each vector with $\ell_1$ regularized regression. Because of the independence of component vectors, FasTR is able to solve in a parallel way and the time complexity is proved to be superior to previous models. We evaluate the performance of FasTR on several simulated datasets and a real-world fMRI dataset. Experiment results show that, compared with four baseline models, in every case, FasTR can compute a better solution within less time.

Sparse and Low-Rank Tensor Regression via Parallel Proximal Method

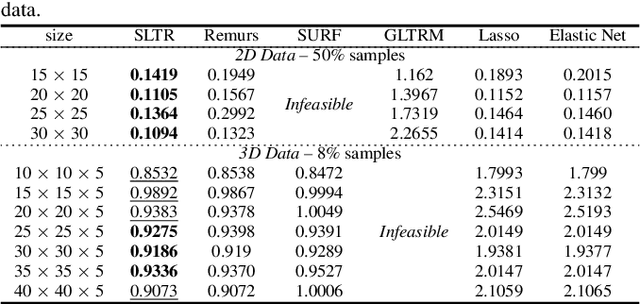
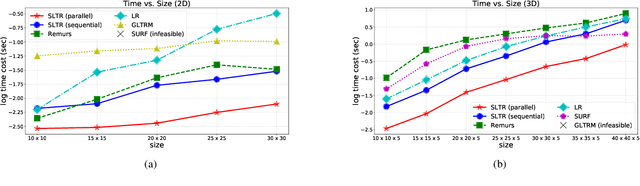
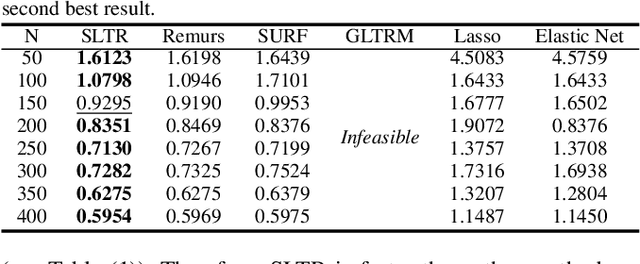
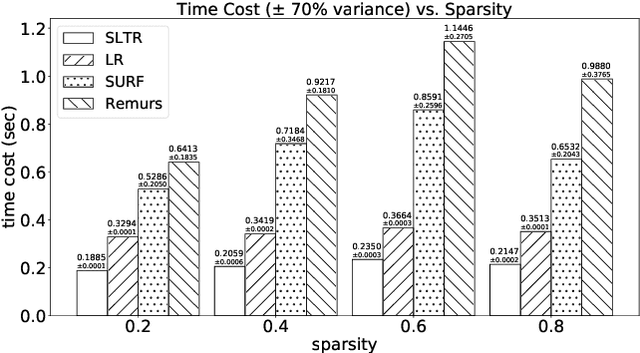
Motivated by applications in various scientific fields having demand of predicting relationship between higher-order (tensor) feature and univariate response, we propose a \underline{S}parse and \underline{L}ow-rank \underline{T}ensor \underline{R}egression model (SLTR). This model enforces sparsity and low-rankness of the tensor coefficient by directly applying $\ell_1$ norm and tensor nuclear norm on it respectively, such that (1) the structural information of tensor is preserved and (2) the data interpretation is convenient. To make the solving procedure scalable and efficient, SLTR makes use of the proximal gradient method to optimize two norm regularizers, which can be easily implemented parallelly. Additionally, a tighter convergence rate is proved over three-order tensor data. We evaluate SLTR on several simulated datasets and one fMRI dataset. Experiment results show that, compared with previous models, SLTR is able to obtain a solution no worse than others with much less time cost.

A Fast and Scalable Joint Estimator for Integrating Additional Knowledge in Learning Multiple Related Sparse Gaussian Graphical Models

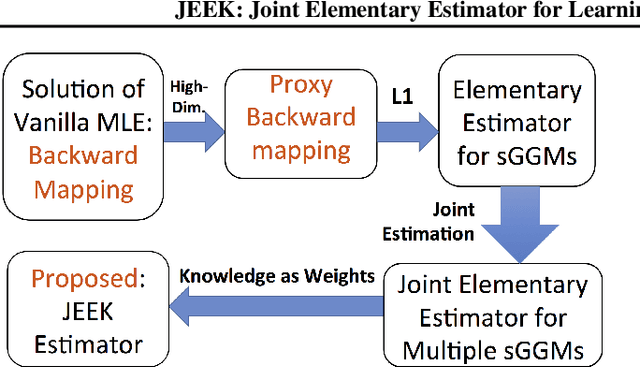
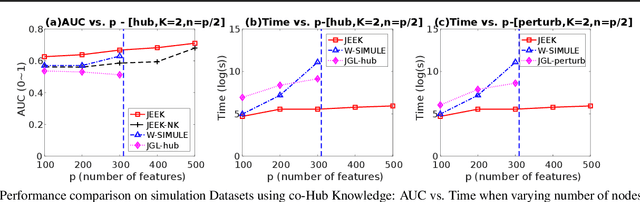
We consider the problem of including additional knowledge in estimating sparse Gaussian graphical models (sGGMs) from aggregated samples, arising often in bioinformatics and neuroimaging applications. Previous joint sGGM estimators either fail to use existing knowledge or cannot scale-up to many tasks (large $K$) under a high-dimensional (large $p$) situation. In this paper, we propose a novel \underline{J}oint \underline{E}lementary \underline{E}stimator incorporating additional \underline{K}nowledge (JEEK) to infer multiple related sparse Gaussian Graphical models from large-scale heterogeneous data. Using domain knowledge as weights, we design a novel hybrid norm as the minimization objective to enforce the superposition of two weighted sparsity constraints, one on the shared interactions and the other on the task-specific structural patterns. This enables JEEK to elegantly consider various forms of existing knowledge based on the domain at hand and avoid the need to design knowledge-specific optimization. JEEK is solved through a fast and entry-wise parallelizable solution that largely improves the computational efficiency of the state-of-the-art $O(p^5K^4)$ to $O(p^2K^4)$. We conduct a rigorous statistical analysis showing that JEEK achieves the same convergence rate $O(\log(Kp)/n_{tot})$ as the state-of-the-art estimators that are much harder to compute. Empirically, on multiple synthetic datasets and two real-world data, JEEK outperforms the speed of the state-of-arts significantly while achieving the same level of prediction accuracy. Available as R tool "jeek"

Fast and Scalable Learning of Sparse Changes in High-Dimensional Gaussian Graphical Model Structure

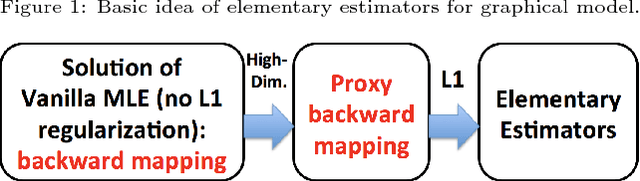
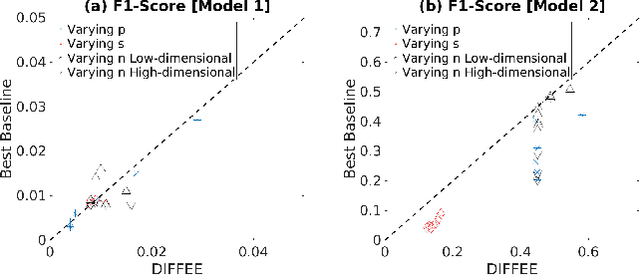
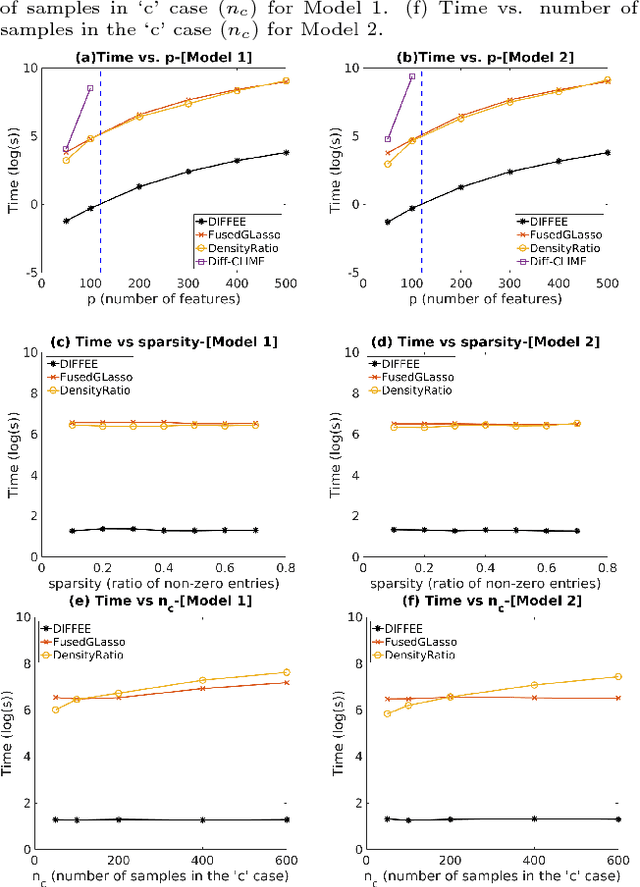
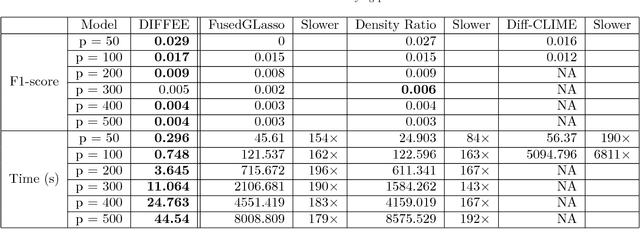
We focus on the problem of estimating the change in the dependency structures of two $p$-dimensional Gaussian Graphical models (GGMs). Previous studies for sparse change estimation in GGMs involve expensive and difficult non-smooth optimization. We propose a novel method, DIFFEE for estimating DIFFerential networks via an Elementary Estimator under a high-dimensional situation. DIFFEE is solved through a faster and closed form solution that enables it to work in large-scale settings. We conduct a rigorous statistical analysis showing that surprisingly DIFFEE achieves the same asymptotic convergence rates as the state-of-the-art estimators that are much more difficult to compute. Our experimental results on multiple synthetic datasets and one real-world data about brain connectivity show strong performance improvements over baselines, as well as significant computational benefits.

A Fast and Scalable Joint Estimator for Learning Multiple Related Sparse Gaussian Graphical Models

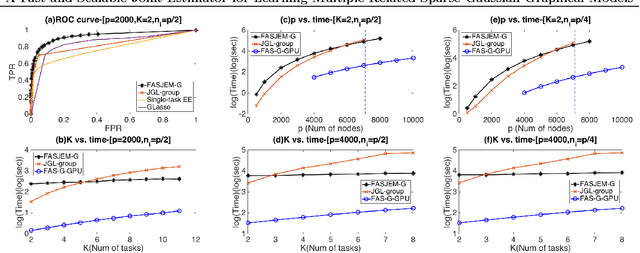
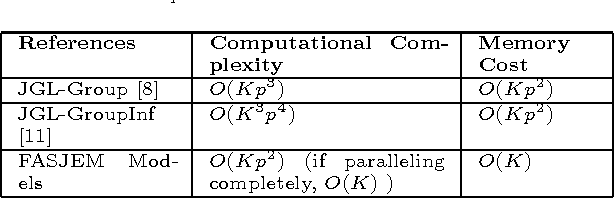
Estimating multiple sparse Gaussian Graphical Models (sGGMs) jointly for many related tasks (large $K$) under a high-dimensional (large $p$) situation is an important task. Most previous studies for the joint estimation of multiple sGGMs rely on penalized log-likelihood estimators that involve expensive and difficult non-smooth optimizations. We propose a novel approach, FASJEM for \underline{fa}st and \underline{s}calable \underline{j}oint structure-\underline{e}stimation of \underline{m}ultiple sGGMs at a large scale. As the first study of joint sGGM using the Elementary Estimator framework, our work has three major contributions: (1) We solve FASJEM through an entry-wise manner which is parallelizable. (2) We choose a proximal algorithm to optimize FASJEM. This improves the computational efficiency from $O(Kp^3)$ to $O(Kp^2)$ and reduces the memory requirement from $O(Kp^2)$ to $O(K)$. (3) We theoretically prove that FASJEM achieves a consistent estimation with a convergence rate of $O(\log(Kp)/n_{tot})$. On several synthetic and four real-world datasets, FASJEM shows significant improvements over baselines on accuracy, computational complexity, and memory costs.

A Theoretical Framework for Robustness of (Deep) Classifiers against Adversarial Examples

Most machine learning classifiers, including deep neural networks, are vulnerable to adversarial examples. Such inputs are typically generated by adding small but purposeful modifications that lead to incorrect outputs while imperceptible to human eyes. The goal of this paper is not to introduce a single method, but to make theoretical steps towards fully understanding adversarial examples. By using concepts from topology, our theoretical analysis brings forth the key reasons why an adversarial example can fool a classifier ($f_1$) and adds its oracle ($f_2$, like human eyes) in such analysis. By investigating the topological relationship between two (pseudo)metric spaces corresponding to predictor $f_1$ and oracle $f_2$, we develop necessary and sufficient conditions that can determine if $f_1$ is always robust (strong-robust) against adversarial examples according to $f_2$. Interestingly our theorems indicate that just one unnecessary feature can make $f_1$ not strong-robust, and the right feature representation learning is the key to getting a classifier that is both accurate and strong-robust.

A Constrained, Weighted-L1 Minimization Approach for Joint Discovery of Heterogeneous Neural Connectivity Graphs

Determining functional brain connectivity is crucial to understanding the brain and neural differences underlying disorders such as autism. Recent studies have used Gaussian graphical models to learn brain connectivity via statistical dependencies across brain regions from neuroimaging. However, previous studies often fail to properly incorporate priors tailored to neuroscience, such as preferring shorter connections. To remedy this problem, the paper here introduces a novel, weighted-$\ell_1$, multi-task graphical model (W-SIMULE). This model elegantly incorporates a flexible prior, along with a parallelizable formulation. Additionally, W-SIMULE extends the often-used Gaussian assumption, leading to considerable performance increases. Here, applications to fMRI data show that W-SIMULE succeeds in determining functional connectivity in terms of (1) log-likelihood, (2) finding edges that differentiate groups, and (3) classifying different groups based on their connectivity, achieving 58.6\% accuracy on the ABIDE dataset. Having established W-SIMULE's effectiveness, it links four key areas to autism, all of which are consistent with the literature. Due to its elegant domain adaptivity, W-SIMULE can be readily applied to various data types to effectively estimate connectivity.

GaKCo: a Fast GApped k-mer string Kernel using COunting

String Kernel (SK) techniques, especially those using gapped $k$-mers as features (gk), have obtained great success in classifying sequences like DNA, protein, and text. However, the state-of-the-art gk-SK runs extremely slow when we increase the dictionary size ($\Sigma$) or allow more mismatches ($M$). This is because current gk-SK uses a trie-based algorithm to calculate co-occurrence of mismatched substrings resulting in a time cost proportional to $O(\Sigma^{M})$. We propose a \textbf{fast} algorithm for calculating \underline{Ga}pped $k$-mer \underline{K}ernel using \underline{Co}unting (GaKCo). GaKCo uses associative arrays to calculate the co-occurrence of substrings using cumulative counting. This algorithm is fast, scalable to larger $\Sigma$ and $M$, and naturally parallelizable. We provide a rigorous asymptotic analysis that compares GaKCo with the state-of-the-art gk-SK. Theoretically, the time cost of GaKCo is independent of the $\Sigma^{M}$ term that slows down the trie-based approach. Experimentally, we observe that GaKCo achieves the same accuracy as the state-of-the-art and outperforms its speed by factors of 2, 100, and 4, on classifying sequences of DNA (5 datasets), protein (12 datasets), and character-based English text (2 datasets), respectively. GaKCo is shared as an open source tool at \url{https://github.com/QData/GaKCo-SVM}