Leveraging tropical reef, bird and unrelated sounds for superior transfer learning in marine bioacoustics

Machine learning has the potential to revolutionize passive acoustic monitoring (PAM) for ecological assessments. However, high annotation and compute costs limit the field's efficacy. Generalizable pretrained networks can overcome these costs, but high-quality pretraining requires vast annotated libraries, limiting its current applicability primarily to bird taxa. Here, we identify the optimum pretraining strategy for a data-deficient domain using coral reef bioacoustics. We assemble ReefSet, a large annotated library of reef sounds, though modest compared to bird libraries at 2% of the sample count. Through testing few-shot transfer learning performance, we observe that pretraining on bird audio provides notably superior generalizability compared to pretraining on ReefSet or unrelated audio alone. However, our key findings show that cross-domain mixing which leverages bird, reef and unrelated audio during pretraining maximizes reef generalizability. SurfPerch, our pretrained network, provides a strong foundation for automated analysis of marine PAM data with minimal annotation and compute costs.

BIRB: A Generalization Benchmark for Information Retrieval in Bioacoustics

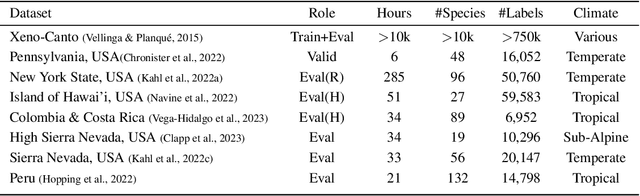
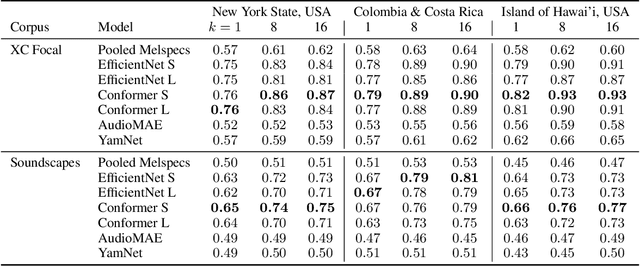
The ability for a machine learning model to cope with differences in training and deployment conditions--e.g. in the presence of distribution shift or the generalization to new classes altogether--is crucial for real-world use cases. However, most empirical work in this area has focused on the image domain with artificial benchmarks constructed to measure individual aspects of generalization. We present BIRB, a complex benchmark centered on the retrieval of bird vocalizations from passively-recorded datasets given focal recordings from a large citizen science corpus available for training. We propose a baseline system for this collection of tasks using representation learning and a nearest-centroid search. Our thorough empirical evaluation and analysis surfaces open research directions, suggesting that BIRB fills the need for a more realistic and complex benchmark to drive progress on robustness to distribution shifts and generalization of ML models.

In Search for a Generalizable Method for Source Free Domain Adaptation

Source-free domain adaptation (SFDA) is compelling because it allows adapting an off-the-shelf model to a new domain using only unlabelled data. In this work, we apply existing SFDA techniques to a challenging set of naturally-occurring distribution shifts in bioacoustics, which are very different from the ones commonly studied in computer vision. We find existing methods perform differently relative to each other than observed in vision benchmarks, and sometimes perform worse than no adaptation at all. We propose a new simple method which outperforms the existing methods on our new shifts while exhibiting strong performance on a range of vision datasets. Our findings suggest that existing SFDA methods are not as generalizable as previously thought and that considering diverse modalities can be a useful avenue for designing more robust models.

GradMax: Growing Neural Networks using Gradient Information

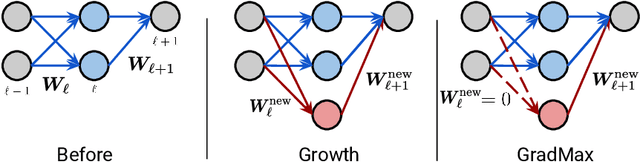
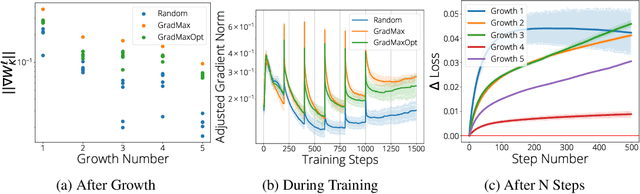
The architecture and the parameters of neural networks are often optimized independently, which requires costly retraining of the parameters whenever the architecture is modified. In this work we instead focus on growing the architecture without requiring costly retraining. We present a method that adds new neurons during training without impacting what is already learned, while improving the training dynamics. We achieve the latter by maximizing the gradients of the new weights and find the optimal initialization efficiently by means of the singular value decomposition (SVD). We call this technique Gradient Maximizing Growth (GradMax) and demonstrate its effectiveness in variety of vision tasks and architectures.

Halting Time is Predictable for Large Models: A Universality Property and Average-case Analysis

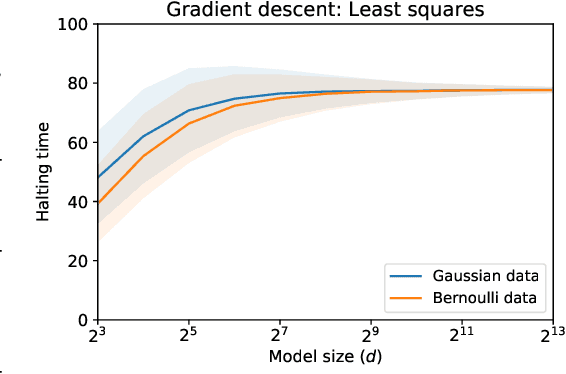
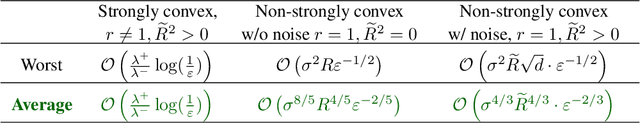
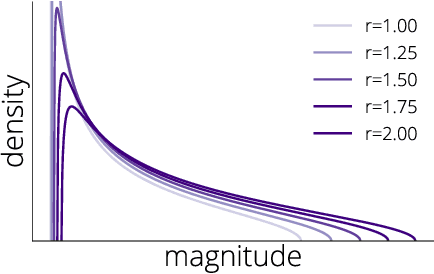
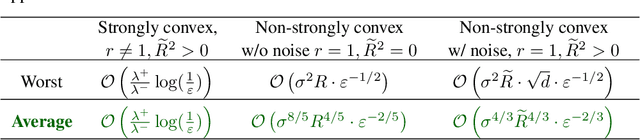
Average-case analysis computes the complexity of an algorithm averaged over all possible inputs. Compared to worst-case analysis, it is more representative of the typical behavior of an algorithm, but remains largely unexplored in optimization. One difficulty is that the analysis can depend on the probability distribution of the inputs to the model. However, we show that this is not the case for a class of large-scale problems trained with gradient descent including random least squares and one-hidden layer neural networks with random weights. In fact, the halting time exhibits a universality property: it is independent of the probability distribution. With this barrier for average-case analysis removed, we provide the first explicit average-case convergence rates showing a tighter complexity not captured by traditional worst-case analysis. Finally, numerical simulations suggest this universality property holds for a more general class of algorithms and problems.

Fast Training of Sparse Graph Neural Networks on Dense Hardware

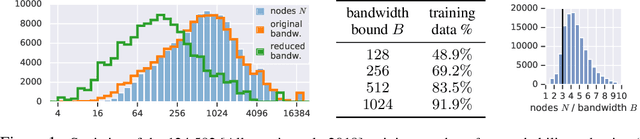
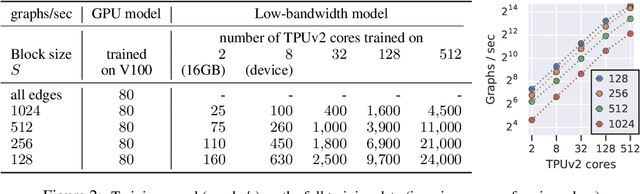
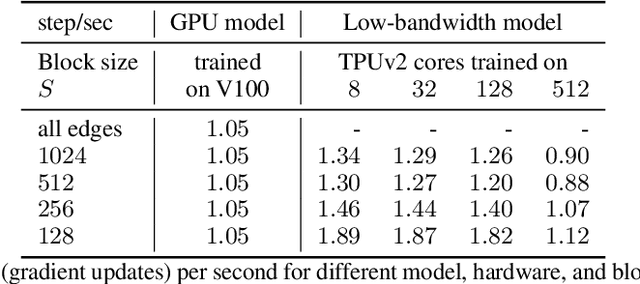
Graph neural networks have become increasingly popular in recent years due to their ability to naturally encode relational input data and their ability to scale to large graphs by operating on a sparse representation of graph adjacency matrices. As we look to scale up these models using custom hardware, a natural assumption would be that we need hardware tailored to sparse operations and/or dynamic control flow. In this work, we question this assumption by scaling up sparse graph neural networks using a platform targeted at dense computation on fixed-size data. Drawing inspiration from optimization of numerical algorithms on sparse matrices, we develop techniques that enable training the sparse graph neural network model from Allamanis et al. [2018] in 13 minutes using a 512-core TPUv2 Pod, whereas the original training takes almost a day.

Information matrices and generalization

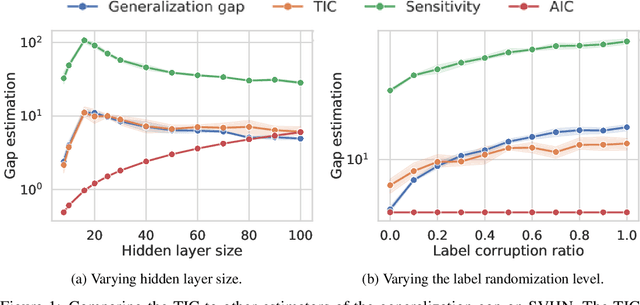
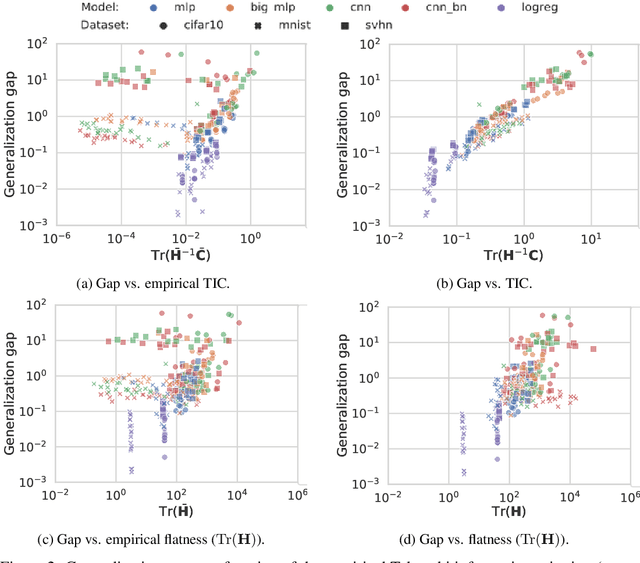
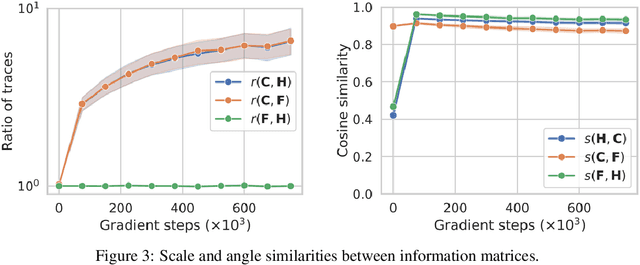
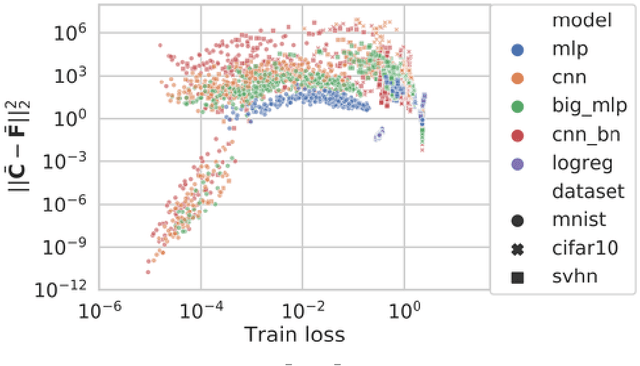
This work revisits the use of information criteria to characterize the generalization of deep learning models. In particular, we empirically demonstrate the effectiveness of the Takeuchi information criterion (TIC), an extension of the Akaike information criterion (AIC) for misspecified models, in estimating the generalization gap, shedding light on why quantities such as the number of parameters cannot quantify generalization. The TIC depends on both the Hessian of the loss H and the covariance of the gradients C. By exploring the similarities and differences between these two matrices as well as the Fisher information matrix F, we study the interplay between noise and curvature in deep models. We also address the question of whether C is a reasonable approximation to F, as is commonly assumed.

Automatic differentiation in ML: Where we are and where we should be going

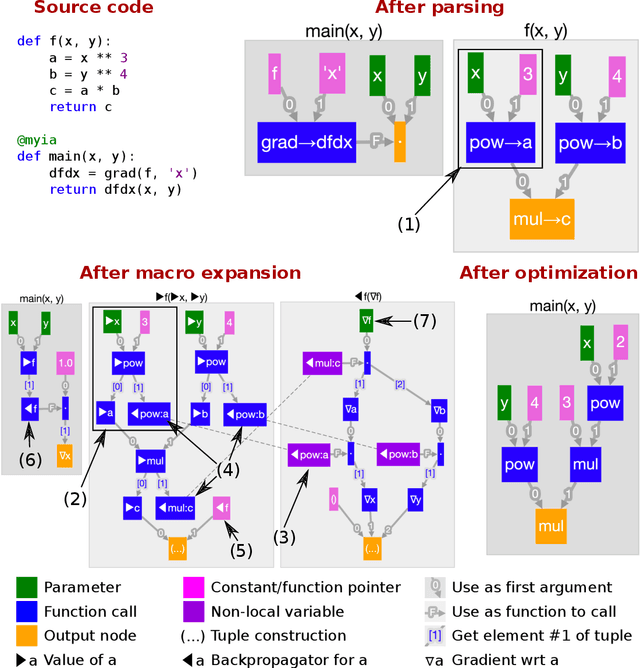
We review the current state of automatic differentiation (AD) for array programming in machine learning (ML), including the different approaches such as operator overloading (OO) and source transformation (ST) used for AD, graph-based intermediate representations for programs, and source languages. Based on these insights, we introduce a new graph-based intermediate representation (IR) which specifically aims to efficiently support fully-general AD for array programming. Unlike existing dataflow programming representations in ML frameworks, our IR naturally supports function calls, higher-order functions and recursion, making ML models easier to implement. The ability to represent closures allows us to perform AD using ST without a tape, making the resulting derivative (adjoint) program amenable to ahead-of-time optimization using tools from functional language compilers, and enabling higher-order derivatives. Lastly, we introduce a proof of concept compiler toolchain called Myia which uses a subset of Python as a front end.

Tangent: Automatic differentiation using source-code transformation for dynamically typed array programming

The need to efficiently calculate first- and higher-order derivatives of increasingly complex models expressed in Python has stressed or exceeded the capabilities of available tools. In this work, we explore techniques from the field of automatic differentiation (AD) that can give researchers expressive power, performance and strong usability. These include source-code transformation (SCT), flexible gradient surgery, efficient in-place array operations, higher-order derivatives as well as mixing of forward and reverse mode AD. We implement and demonstrate these ideas in the Tangent software library for Python, the first AD framework for a dynamic language that uses SCT.

Tangent: Automatic Differentiation Using Source Code Transformation in Python

Automatic differentiation (AD) is an essential primitive for machine learning programming systems. Tangent is a new library that performs AD using source code transformation (SCT) in Python. It takes numeric functions written in a syntactic subset of Python and NumPy as input, and generates new Python functions which calculate a derivative. This approach to automatic differentiation is different from existing packages popular in machine learning, such as TensorFlow and Autograd. Advantages are that Tangent generates gradient code in Python which is readable by the user, easy to understand and debug, and has no runtime overhead. Tangent also introduces abstractions for easily injecting logic into the generated gradient code, further improving usability.