AlphaEvolve: A coding agent for scientific and algorithmic discovery

In this white paper, we present AlphaEvolve, an evolutionary coding agent that substantially enhances capabilities of state-of-the-art LLMs on highly challenging tasks such as tackling open scientific problems or optimizing critical pieces of computational infrastructure. AlphaEvolve orchestrates an autonomous pipeline of LLMs, whose task is to improve an algorithm by making direct changes to the code. Using an evolutionary approach, continuously receiving feedback from one or more evaluators, AlphaEvolve iteratively improves the algorithm, potentially leading to new scientific and practical discoveries. We demonstrate the broad applicability of this approach by applying it to a number of important computational problems. When applied to optimizing critical components of large-scale computational stacks at Google, AlphaEvolve developed a more efficient scheduling algorithm for data centers, found a functionally equivalent simplification in the circuit design of hardware accelerators, and accelerated the training of the LLM underpinning AlphaEvolve itself. Furthermore, AlphaEvolve discovered novel, provably correct algorithms that surpass state-of-the-art solutions on a spectrum of problems in mathematics and computer science, significantly expanding the scope of prior automated discovery methods (Romera-Paredes et al., 2023). Notably, AlphaEvolve developed a search algorithm that found a procedure to multiply two $4 \times 4$ complex-valued matrices using $48$ scalar multiplications; offering the first improvement, after 56 years, over Strassen's algorithm in this setting. We believe AlphaEvolve and coding agents like it can have a significant impact in improving solutions of problems across many areas of science and computation.

Amplifying human performance in combinatorial competitive programming

Recent years have seen a significant surge in complex AI systems for competitive programming, capable of performing at admirable levels against human competitors. While steady progress has been made, the highest percentiles still remain out of reach for these methods on standard competition platforms such as Codeforces. Here we instead focus on combinatorial competitive programming, where the target is to find as-good-as-possible solutions to otherwise computationally intractable problems, over specific given inputs. We hypothesise that this scenario offers a unique testbed for human-AI synergy, as human programmers can write a backbone of a heuristic solution, after which AI can be used to optimise the scoring function used by the heuristic. We deploy our approach on previous iterations of Hash Code, a global team programming competition inspired by NP-hard software engineering problems at Google, and we leverage FunSearch to evolve our scoring functions. Our evolved solutions significantly improve the attained scores from their baseline, successfully breaking into the top percentile on all previous Hash Code online qualification rounds, and outperforming the top human teams on several. Our method is also performant on an optimisation problem that featured in a recent held-out AtCoder contest.

Quantum Circuit Optimization with AlphaTensor

A key challenge in realizing fault-tolerant quantum computers is circuit optimization. Focusing on the most expensive gates in fault-tolerant quantum computation (namely, the T gates), we address the problem of T-count optimization, i.e., minimizing the number of T gates that are needed to implement a given circuit. To achieve this, we develop AlphaTensor-Quantum, a method based on deep reinforcement learning that exploits the relationship between optimizing T-count and tensor decomposition. Unlike existing methods for T-count optimization, AlphaTensor-Quantum can incorporate domain-specific knowledge about quantum computation and leverage gadgets, which significantly reduces the T-count of the optimized circuits. AlphaTensor-Quantum outperforms the existing methods for T-count optimization on a set of arithmetic benchmarks (even when compared without making use of gadgets). Remarkably, it discovers an efficient algorithm akin to Karatsuba's method for multiplication in finite fields. AlphaTensor-Quantum also finds the best human-designed solutions for relevant arithmetic computations used in Shor's algorithm and for quantum chemistry simulation, thus demonstrating it can save hundreds of hours of research by optimizing relevant quantum circuits in a fully automated way.

Finding Increasingly Large Extremal Graphs with AlphaZero and Tabu Search

This work studies a central extremal graph theory problem inspired by a 1975 conjecture of Erd\H{o}s, which aims to find graphs with a given size (number of nodes) that maximize the number of edges without having 3- or 4-cycles. We formulate this problem as a sequential decision-making problem and compare AlphaZero, a neural network-guided tree search, with tabu search, a heuristic local search method. Using either method, by introducing a curriculum -- jump-starting the search for larger graphs using good graphs found at smaller sizes -- we improve the state-of-the-art lower bounds for several sizes. We also propose a flexible graph-generation environment and a permutation-invariant network architecture for learning to search in the space of graphs.

Neural Program Synthesis with a Differentiable Fixer

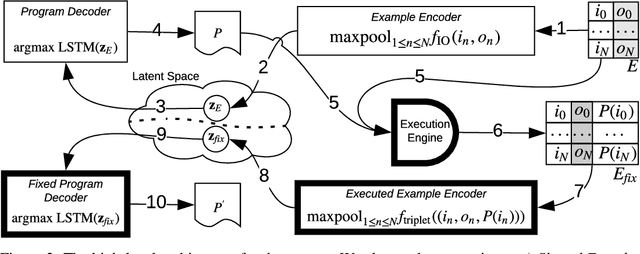
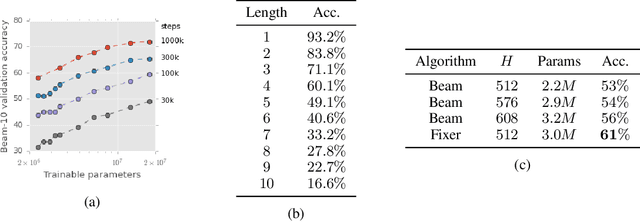
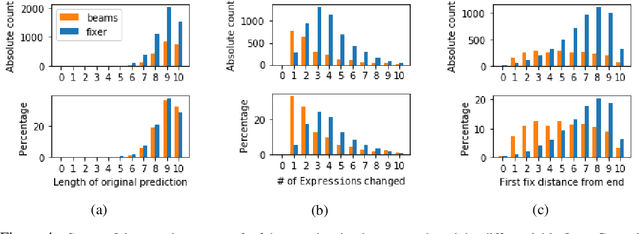
We present a new program synthesis approach that combines an encoder-decoder based synthesis architecture with a differentiable program fixer. Our approach is inspired from the fact that human developers seldom get their program correct on the first attempt, and perform iterative testing-based program fixing to get to the desired program functionality. Similarly, our approach first learns a distribution over programs conditioned on an encoding of a set of input-output examples, and then iteratively performs fix operations using the differentiable fixer. The fixer takes as input the original examples and the current program's outputs on example inputs, and generates a new distribution over the programs with the goal of reducing the discrepancies between the current program outputs and the desired example outputs. We train our architecture end-to-end on the RobustFill domain, and show that the addition of the fixer module leads to a significant improvement on synthesis accuracy compared to using beam search.

Fast Training of Sparse Graph Neural Networks on Dense Hardware

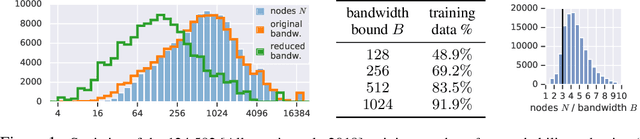
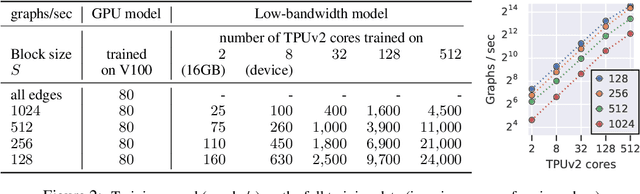
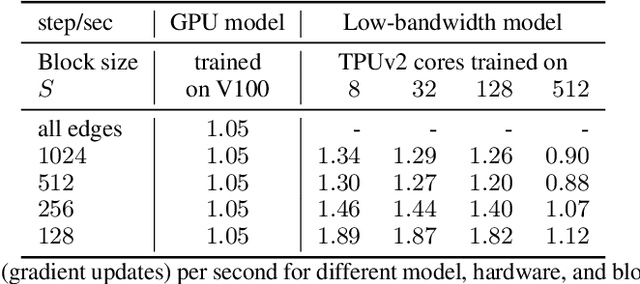
Graph neural networks have become increasingly popular in recent years due to their ability to naturally encode relational input data and their ability to scale to large graphs by operating on a sparse representation of graph adjacency matrices. As we look to scale up these models using custom hardware, a natural assumption would be that we need hardware tailored to sparse operations and/or dynamic control flow. In this work, we question this assumption by scaling up sparse graph neural networks using a platform targeted at dense computation on fixed-size data. Drawing inspiration from optimization of numerical algorithms on sparse matrices, we develop techniques that enable training the sparse graph neural network model from Allamanis et al. [2018] in 13 minutes using a 512-core TPUv2 Pod, whereas the original training takes almost a day.

Differentially Private Database Release via Kernel Mean Embeddings

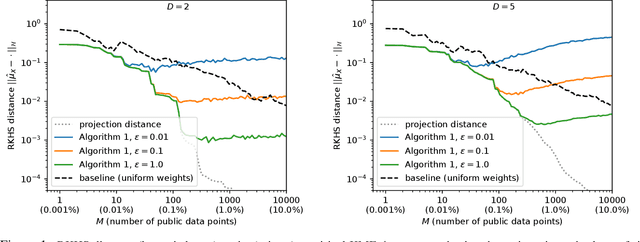
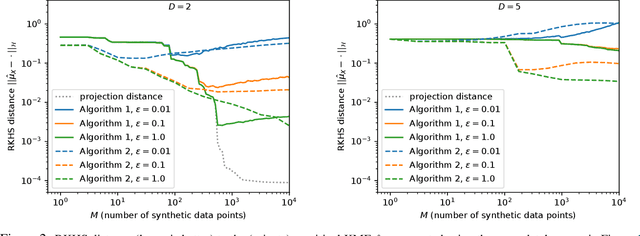
We lay theoretical foundations for new database release mechanisms that allow third-parties to construct consistent estimators of population statistics, while ensuring that the privacy of each individual contributing to the database is protected. The proposed framework rests on two main ideas. First, releasing (an estimate of) the kernel mean embedding of the data generating random variable instead of the database itself still allows third-parties to construct consistent estimators of a wide class of population statistics. Second, the algorithm can satisfy the definition of differential privacy by basing the released kernel mean embedding on entirely synthetic data points, while controlling accuracy through the metric available in a Reproducing Kernel Hilbert Space. We describe two instantiations of the proposed framework, suitable under different scenarios, and prove theoretical results guaranteeing differential privacy of the resulting algorithms and the consistency of estimators constructed from their outputs.

Lost Relatives of the Gumbel Trick

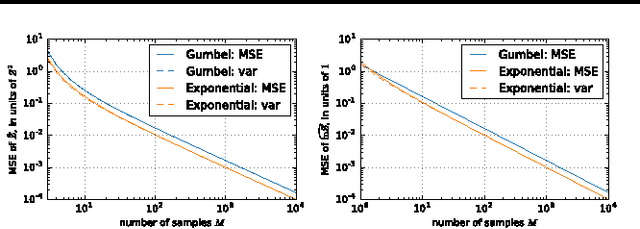
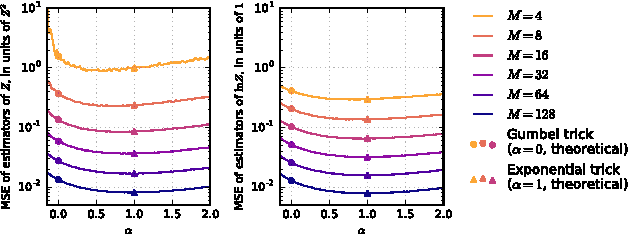
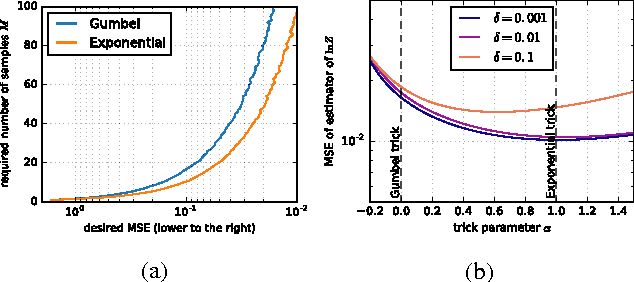
The Gumbel trick is a method to sample from a discrete probability distribution, or to estimate its normalizing partition function. The method relies on repeatedly applying a random perturbation to the distribution in a particular way, each time solving for the most likely configuration. We derive an entire family of related methods, of which the Gumbel trick is one member, and show that the new methods have superior properties in several settings with minimal additional computational cost. In particular, for the Gumbel trick to yield computational benefits for discrete graphical models, Gumbel perturbations on all configurations are typically replaced with so-called low-rank perturbations. We show how a subfamily of our new methods adapts to this setting, proving new upper and lower bounds on the log partition function and deriving a family of sequential samplers for the Gibbs distribution. Finally, we balance the discussion by showing how the simpler analytical form of the Gumbel trick enables additional theoretical results.

DeepCoder: Learning to Write Programs

We develop a first line of attack for solving programming competition-style problems from input-output examples using deep learning. The approach is to train a neural network to predict properties of the program that generated the outputs from the inputs. We use the neural network's predictions to augment search techniques from the programming languages community, including enumerative search and an SMT-based solver. Empirically, we show that our approach leads to an order of magnitude speedup over the strong non-augmented baselines and a Recurrent Neural Network approach, and that we are able to solve problems of difficulty comparable to the simplest problems on programming competition websites.

The Mondrian Kernel

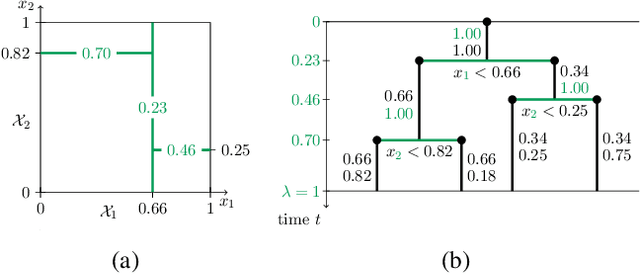
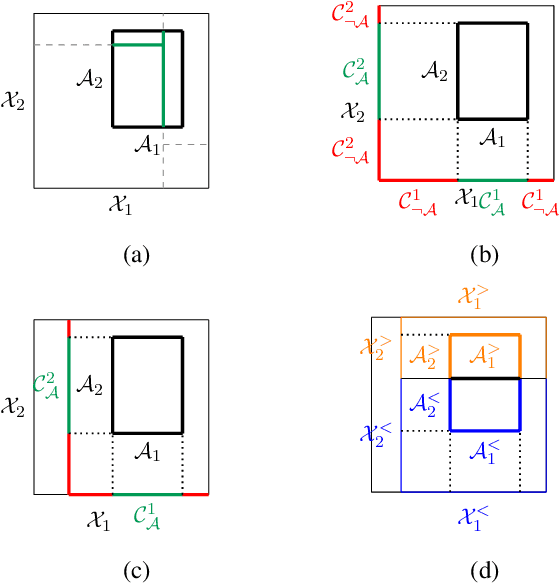
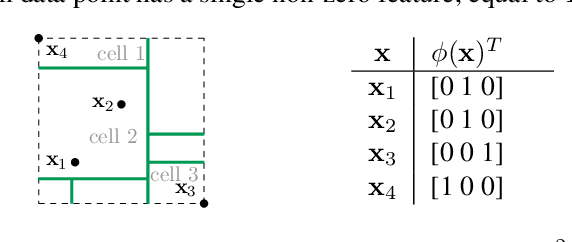
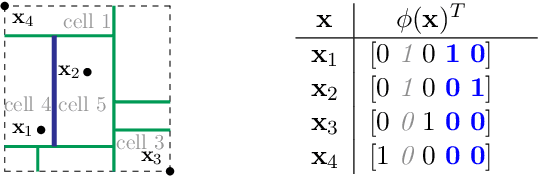
We introduce the Mondrian kernel, a fast random feature approximation to the Laplace kernel. It is suitable for both batch and online learning, and admits a fast kernel-width-selection procedure as the random features can be re-used efficiently for all kernel widths. The features are constructed by sampling trees via a Mondrian process [Roy and Teh, 2009], and we highlight the connection to Mondrian forests [Lakshminarayanan et al., 2014], where trees are also sampled via a Mondrian process, but fit independently. This link provides a new insight into the relationship between kernel methods and random forests.