The High Line: Exact Risk and Learning Rate Curves of Stochastic Adaptive Learning Rate Algorithms

We develop a framework for analyzing the training and learning rate dynamics on a large class of high-dimensional optimization problems, which we call the high line, trained using one-pass stochastic gradient descent (SGD) with adaptive learning rates. We give exact expressions for the risk and learning rate curves in terms of a deterministic solution to a system of ODEs. We then investigate in detail two adaptive learning rates -- an idealized exact line search and AdaGrad-Norm -- on the least squares problem. When the data covariance matrix has strictly positive eigenvalues, this idealized exact line search strategy can exhibit arbitrarily slower convergence when compared to the optimal fixed learning rate with SGD. Moreover we exactly characterize the limiting learning rate (as time goes to infinity) for line search in the setting where the data covariance has only two distinct eigenvalues. For noiseless targets, we further demonstrate that the AdaGrad-Norm learning rate converges to a deterministic constant inversely proportional to the average eigenvalue of the data covariance matrix, and identify a phase transition when the covariance density of eigenvalues follows a power law distribution.

4+3 Phases of Compute-Optimal Neural Scaling Laws

We consider the three parameter solvable neural scaling model introduced by Maloney, Roberts, and Sully. The model has three parameters: data complexity, target complexity, and model-parameter-count. We use this neural scaling model to derive new predictions about the compute-limited, infinite-data scaling law regime. To train the neural scaling model, we run one-pass stochastic gradient descent on a mean-squared loss. We derive a representation of the loss curves which holds over all iteration counts and improves in accuracy as the model parameter count grows. We then analyze the compute-optimal model-parameter-count, and identify 4 phases (+3 subphases) in the data-complexity/target-complexity phase-plane. The phase boundaries are determined by the relative importance of model capacity, optimizer noise, and embedding of the features. We furthermore derive, with mathematical proof and extensive numerical evidence, the scaling-law exponents in all of these phases, in particular computing the optimal model-parameter-count as a function of floating point operation budget.

Mirror Descent Algorithms with Nearly Dimension-Independent Rates for Differentially-Private Stochastic Saddle-Point Problems

We study the problem of differentially-private (DP) stochastic (convex-concave) saddle-points in the polyhedral setting. We propose $(\varepsilon, \delta)$-DP algorithms based on stochastic mirror descent that attain nearly dimension-independent convergence rates for the expected duality gap, a type of guarantee that was known before only for bilinear objectives. For convex-concave and first-order-smooth stochastic objectives, our algorithms attain a rate of $\sqrt{\log(d)/n} + (\log(d)^{3/2}/[n\varepsilon])^{1/3}$, where $d$ is the dimension of the problem and $n$ the dataset size. Under an additional second-order-smoothness assumption, we improve the rate on the expected gap to $\sqrt{\log(d)/n} + (\log(d)^{3/2}/[n\varepsilon])^{2/5}$. Under this additional assumption, we also show, by using bias-reduced gradient estimators, that the duality gap is bounded by $\log(d)/\sqrt{n} + \log(d)/[n\varepsilon]^{1/2}$ with constant success probability. This result provides evidence of the near-optimality of the approach. Finally, we show that combining our methods with acceleration techniques from online learning leads to the first algorithm for DP Stochastic Convex Optimization in the polyhedral setting that is not based on Frank-Wolfe methods. For convex and first-order-smooth stochastic objectives, our algorithms attain an excess risk of $\sqrt{\log(d)/n} + \log(d)^{7/10}/[n\varepsilon]^{2/5}$, and when additionally assuming second-order-smoothness, we improve the rate to $\sqrt{\log(d)/n} + \log(d)/\sqrt{n\varepsilon}$. Instrumental to all of these results are various extensions of the classical Maurey Sparsification Lemma, which may be of independent interest.

Implicit Diffusion: Efficient Optimization through Stochastic Sampling

We present a new algorithm to optimize distributions defined implicitly by parameterized stochastic diffusions. Doing so allows us to modify the outcome distribution of sampling processes by optimizing over their parameters. We introduce a general framework for first-order optimization of these processes, that performs jointly, in a single loop, optimization and sampling steps. This approach is inspired by recent advances in bilevel optimization and automatic implicit differentiation, leveraging the point of view of sampling as optimization over the space of probability distributions. We provide theoretical guarantees on the performance of our method, as well as experimental results demonstrating its effectiveness in real-world settings.

Hitting the High-Dimensional Notes: An ODE for SGD learning dynamics on GLMs and multi-index models

We analyze the dynamics of streaming stochastic gradient descent (SGD) in the high-dimensional limit when applied to generalized linear models and multi-index models (e.g. logistic regression, phase retrieval) with general data-covariance. In particular, we demonstrate a deterministic equivalent of SGD in the form of a system of ordinary differential equations that describes a wide class of statistics, such as the risk and other measures of sub-optimality. This equivalence holds with overwhelming probability when the model parameter count grows proportionally to the number of data. This framework allows us to obtain learning rate thresholds for stability of SGD as well as convergence guarantees. In addition to the deterministic equivalent, we introduce an SDE with a simplified diffusion coefficient (homogenized SGD) which allows us to analyze the dynamics of general statistics of SGD iterates. Finally, we illustrate this theory on some standard examples and show numerical simulations which give an excellent match to the theory.

Only Tails Matter: Average-Case Universality and Robustness in the Convex Regime

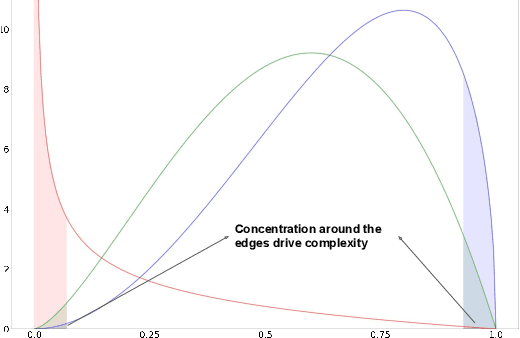
The recently developed average-case analysis of optimization methods allows a more fine-grained and representative convergence analysis than usual worst-case results. In exchange, this analysis requires a more precise hypothesis over the data generating process, namely assuming knowledge of the expected spectral distribution (ESD) of the random matrix associated with the problem. This work shows that the concentration of eigenvalues near the edges of the ESD determines a problem's asymptotic average complexity. This a priori information on this concentration is a more grounded assumption than complete knowledge of the ESD. This approximate concentration is effectively a middle ground between the coarseness of the worst-case scenario convergence and the restrictive previous average-case analysis. We also introduce the Generalized Chebyshev method, asymptotically optimal under a hypothesis on this concentration and globally optimal when the ESD follows a Beta distribution. We compare its performance to classical optimization algorithms, such as gradient descent or Nesterov's scheme, and we show that, in the average-case context, Nesterov's method is universally nearly optimal asymptotically.

Implicit Regularization or Implicit Conditioning? Exact Risk Trajectories of SGD in High Dimensions

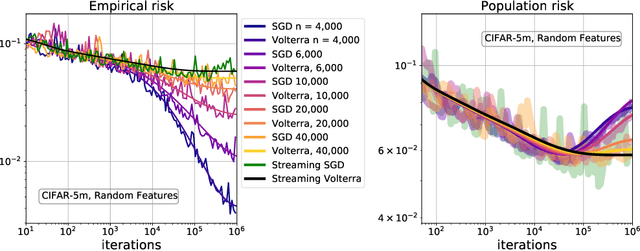
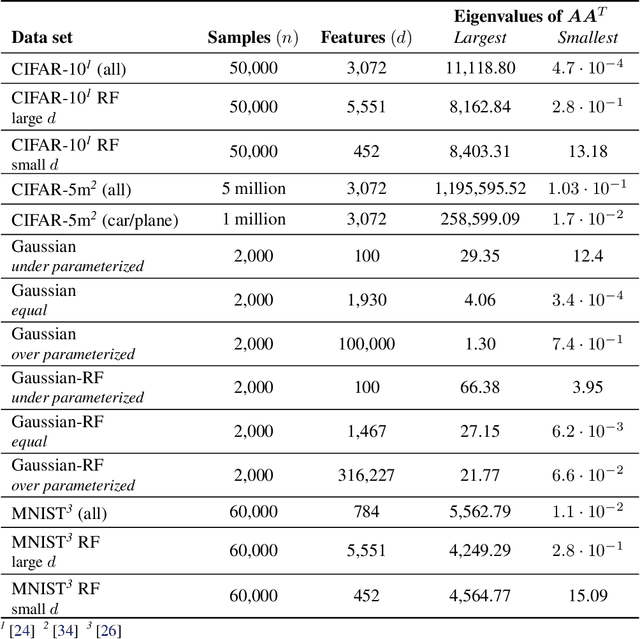
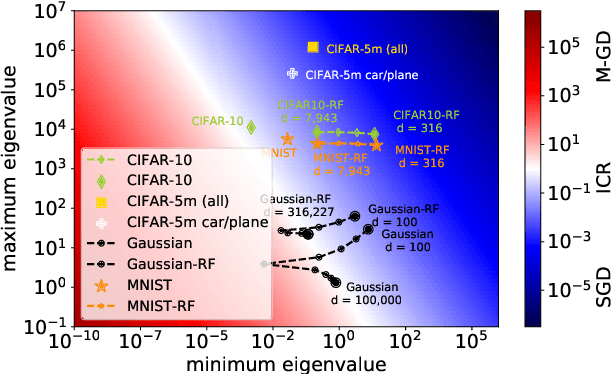
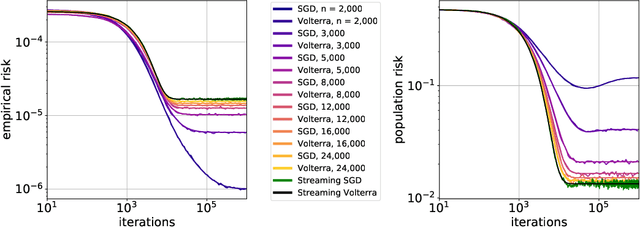
Stochastic gradient descent (SGD) is a pillar of modern machine learning, serving as the go-to optimization algorithm for a diverse array of problems. While the empirical success of SGD is often attributed to its computational efficiency and favorable generalization behavior, neither effect is well understood and disentangling them remains an open problem. Even in the simple setting of convex quadratic problems, worst-case analyses give an asymptotic convergence rate for SGD that is no better than full-batch gradient descent (GD), and the purported implicit regularization effects of SGD lack a precise explanation. In this work, we study the dynamics of multi-pass SGD on high-dimensional convex quadratics and establish an asymptotic equivalence to a stochastic differential equation, which we call homogenized stochastic gradient descent (HSGD), whose solutions we characterize explicitly in terms of a Volterra integral equation. These results yield precise formulas for the learning and risk trajectories, which reveal a mechanism of implicit conditioning that explains the efficiency of SGD relative to GD. We also prove that the noise from SGD negatively impacts generalization performance, ruling out the possibility of any type of implicit regularization in this context. Finally, we show how to adapt the HSGD formalism to include streaming SGD, which allows us to produce an exact prediction for the excess risk of multi-pass SGD relative to that of streaming SGD (bootstrap risk).

Trajectory of Mini-Batch Momentum: Batch Size Saturation and Convergence in High Dimensions

We analyze the dynamics of large batch stochastic gradient descent with momentum (SGD+M) on the least squares problem when both the number of samples and dimensions are large. In this setting, we show that the dynamics of SGD+M converge to a deterministic discrete Volterra equation as dimension increases, which we analyze. We identify a stability measurement, the implicit conditioning ratio (ICR), which regulates the ability of SGD+M to accelerate the algorithm. When the batch size exceeds this ICR, SGD+M converges linearly at a rate of $\mathcal{O}(1/\sqrt{\kappa})$, matching optimal full-batch momentum (in particular performing as well as a full-batch but with a fraction of the size). For batch sizes smaller than the ICR, in contrast, SGD+M has rates that scale like a multiple of the single batch SGD rate. We give explicit choices for the learning rate and momentum parameter in terms of the Hessian spectra that achieve this performance.

Homogenization of SGD in high-dimensions: Exact dynamics and generalization properties

We develop a stochastic differential equation, called homogenized SGD, for analyzing the dynamics of stochastic gradient descent (SGD) on a high-dimensional random least squares problem with $\ell^2$-regularization. We show that homogenized SGD is the high-dimensional equivalence of SGD -- for any quadratic statistic (e.g., population risk with quadratic loss), the statistic under the iterates of SGD converges to the statistic under homogenized SGD when the number of samples $n$ and number of features $d$ are polynomially related ($d^c < n < d^{1/c}$ for some $c > 0$). By analyzing homogenized SGD, we provide exact non-asymptotic high-dimensional expressions for the generalization performance of SGD in terms of a solution of a Volterra integral equation. Further we provide the exact value of the limiting excess risk in the case of quadratic losses when trained by SGD. The analysis is formulated for data matrices and target vectors that satisfy a family of resolvent conditions, which can roughly be viewed as a weak (non-quantitative) form of delocalization of sample-side singular vectors of the data. Several motivating applications are provided including sample covariance matrices with independent samples and random features with non-generative model targets.

Dynamics of Stochastic Momentum Methods on Large-scale, Quadratic Models

We analyze a class of stochastic gradient algorithms with momentum on a high-dimensional random least squares problem. Our framework, inspired by random matrix theory, provides an exact (deterministic) characterization for the sequence of loss values produced by these algorithms which is expressed only in terms of the eigenvalues of the Hessian. This leads to simple expressions for nearly-optimal hyperparameters, a description of the limiting neighborhood, and average-case complexity. As a consequence, we show that (small-batch) stochastic heavy-ball momentum with a fixed momentum parameter provides no actual performance improvement over SGD when step sizes are adjusted correctly. For contrast, in the non-strongly convex setting, it is possible to get a large improvement over SGD using momentum. By introducing hyperparameters that depend on the number of samples, we propose a new algorithm sDANA (stochastic dimension adjusted Nesterov acceleration) which obtains an asymptotically optimal average-case complexity while remaining linearly convergent in the strongly convex setting without adjusting parameters.