Quantum Multiple Kernel Learning

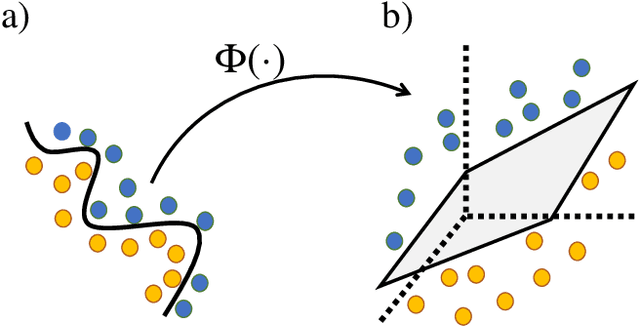
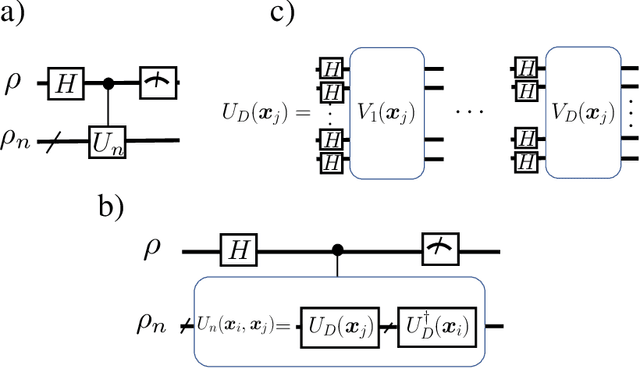
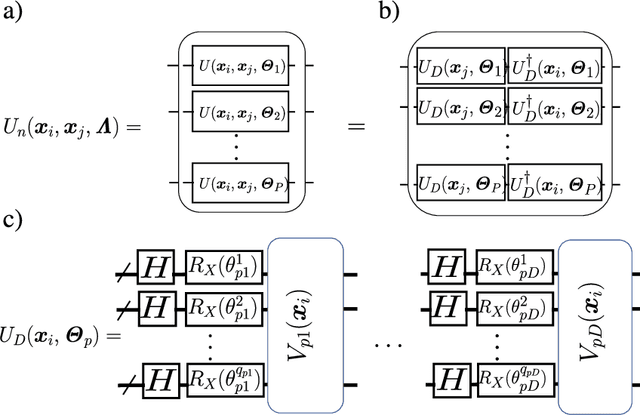
Kernel methods play an important role in machine learning applications due to their conceptual simplicity and superior performance on numerous machine learning tasks. Expressivity of a machine learning model, referring to the ability of the model to approximate complex functions, has a significant influence on its performance in these tasks. One approach to enhancing the expressivity of kernel machines is to combine multiple individual kernels to arrive at a more expressive combined kernel. This approach is referred to as multiple kernel learning (MKL). In this work, we propose an MKL method we refer to as quantum MKL, which combines multiple quantum kernels. Our method leverages the power of deterministic quantum computing with one qubit (DQC1) to estimate the combined kernel for a set of classically intractable individual quantum kernels. The combined kernel estimation is achieved without explicitly computing each individual kernel, while still allowing for the tuning of individual kernels in order to achieve better expressivity. Our simulations on two binary classification problems---one performed on a synthetic dataset and the other on a German credit dataset---demonstrate the superiority of the quantum MKL method over single quantum kernel machines.

A Quantum Annealing-Based Approach to Extreme Clustering

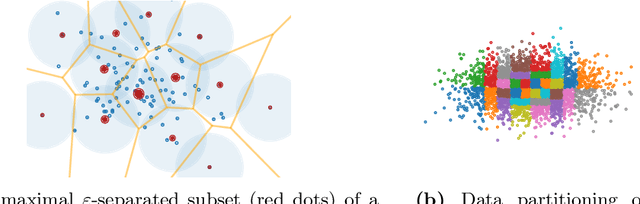
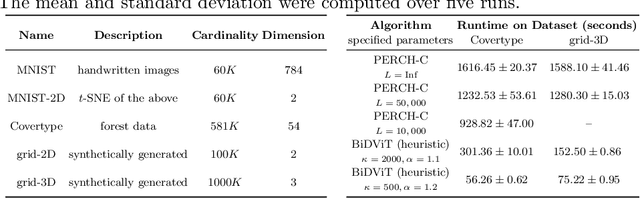
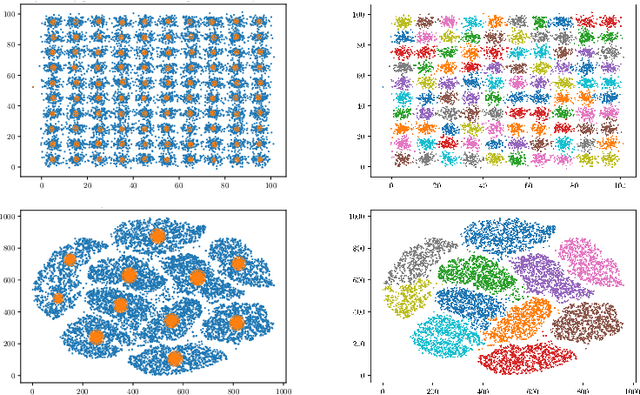
There is a growing need for algorithms and techniques capable of organizing big data in an accurate and efficient manner. Clustering, or grouping dataset elements based on similarity, can be computationally expensive, especially when employed on massive datasets to divide them into a relatively large number of groups. The task of clustering what can amount to millions (billions) of data points into thousands (millions) of clusters is referred to as $\textit{extreme clustering}$. We have devised a distributed method that can be employed to efficiently solve extreme clustering problems using a quantum annealer.

Free energy-based reinforcement learning using a quantum processor

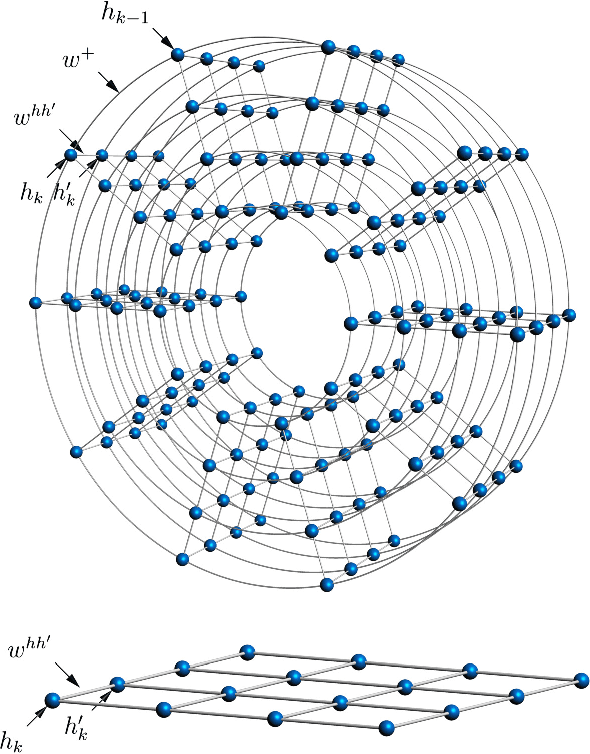
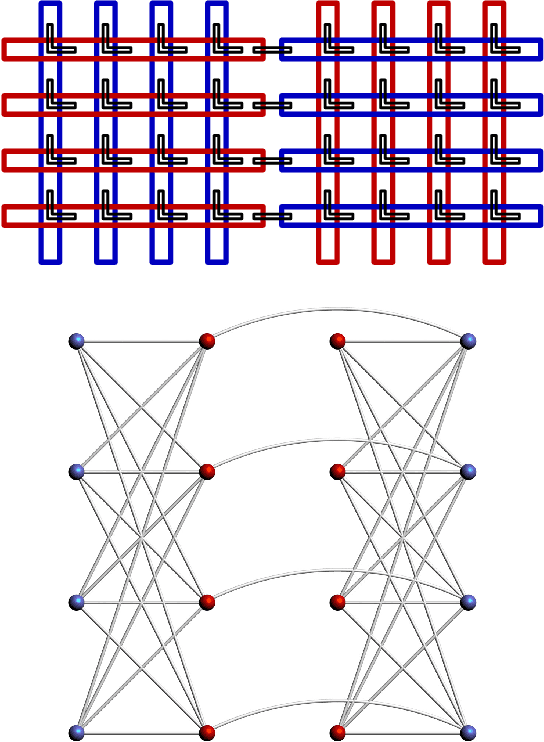
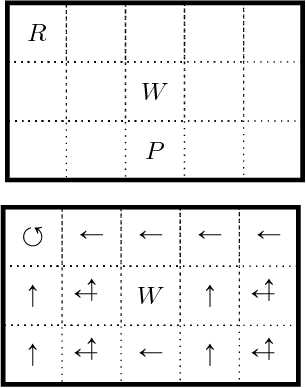
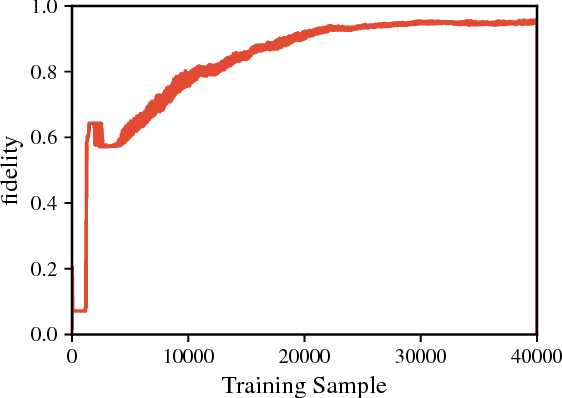
Recent theoretical and experimental results suggest the possibility of using current and near-future quantum hardware in challenging sampling tasks. In this paper, we introduce free energy-based reinforcement learning (FERL) as an application of quantum hardware. We propose a method for processing a quantum annealer's measured qubit spin configurations in approximating the free energy of a quantum Boltzmann machine (QBM). We then apply this method to perform reinforcement learning on the grid-world problem using the D-Wave 2000Q quantum annealer. The experimental results show that our technique is a promising method for harnessing the power of quantum sampling in reinforcement learning tasks.

Reinforcement Learning Using Quantum Boltzmann Machines

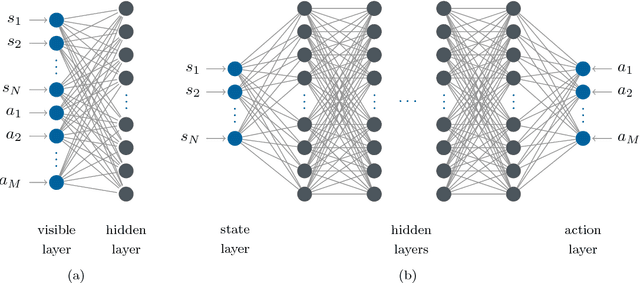
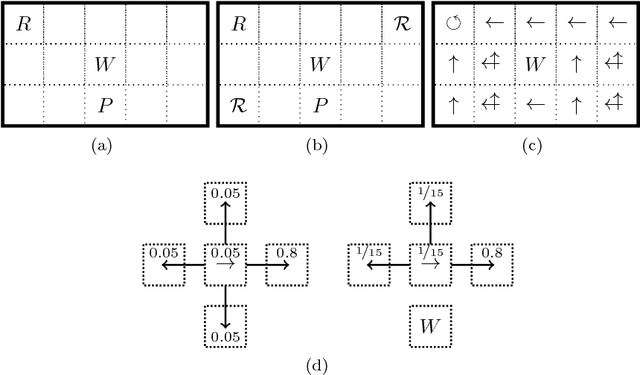
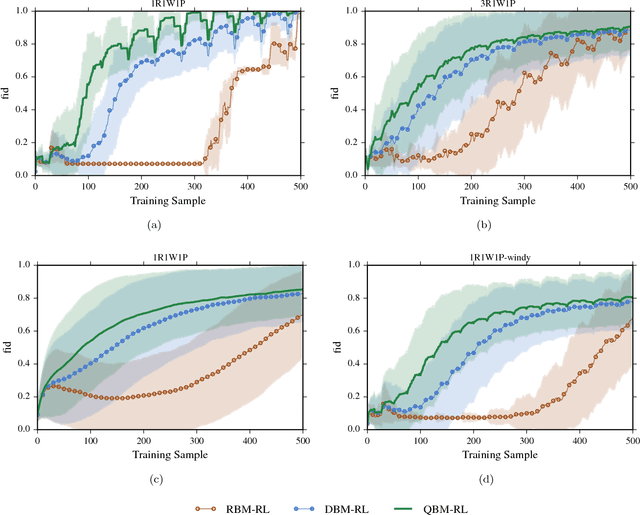
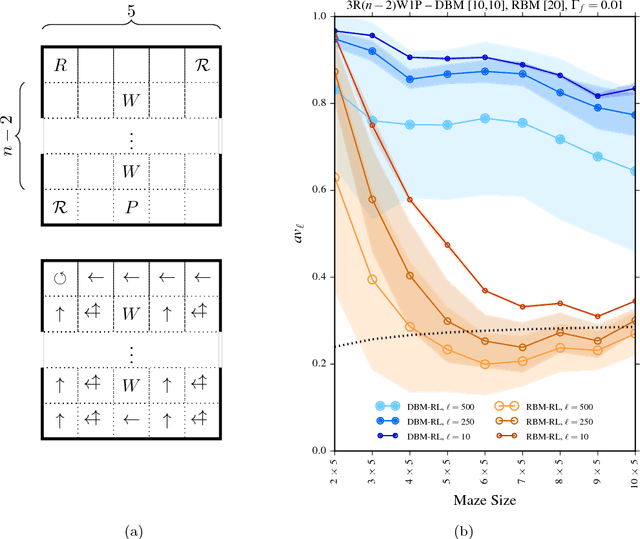
We investigate whether quantum annealers with select chip layouts can outperform classical computers in reinforcement learning tasks. We associate a transverse field Ising spin Hamiltonian with a layout of qubits similar to that of a deep Boltzmann machine (DBM) and use simulated quantum annealing (SQA) to numerically simulate quantum sampling from this system. We design a reinforcement learning algorithm in which the set of visible nodes representing the states and actions of an optimal policy are the first and last layers of the deep network. In absence of a transverse field, our simulations show that DBMs train more effectively than restricted Boltzmann machines (RBM) with the same number of weights. Since sampling from Boltzmann distributions of a DBM is not classically feasible, this is evidence of advantage of a non-Turing sampling oracle. We then develop a framework for training the network as a quantum Boltzmann machine (QBM) in the presence of a significant transverse field for reinforcement learning. This further improves the reinforcement learning method using DBMs.