Estimating Network Models using Neural Networks

Exponential random graph models (ERGMs) are very flexible for modeling network formation but pose difficult estimation challenges due to their intractable normalizing constant. Existing methods, such as MCMC-MLE, rely on sequential simulation at every optimization step. We propose a neural network approach that trains on a single, large set of parameter-simulation pairs to learn the mapping from parameters to average network statistics. Once trained, this map can be inverted, yielding a fast and parallelizable estimation method. The procedure also accommodates extra network statistics to mitigate model misspecification. Some simple illustrative examples show that the method performs well in practice.

On identifying unobserved heterogeneity in stochastic blockmodel graphs with vertex covariates

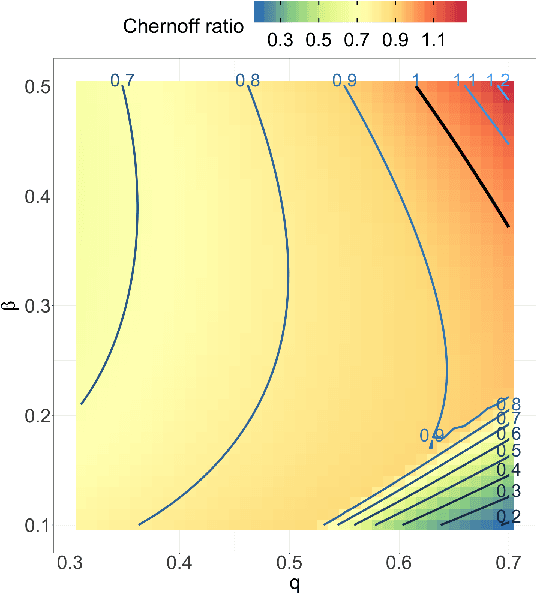
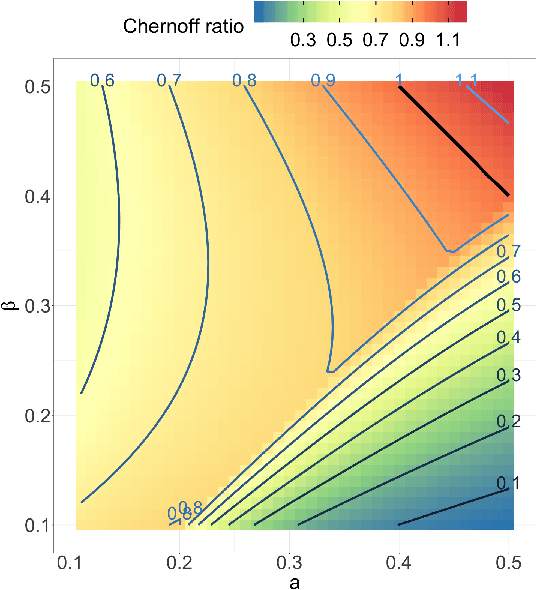
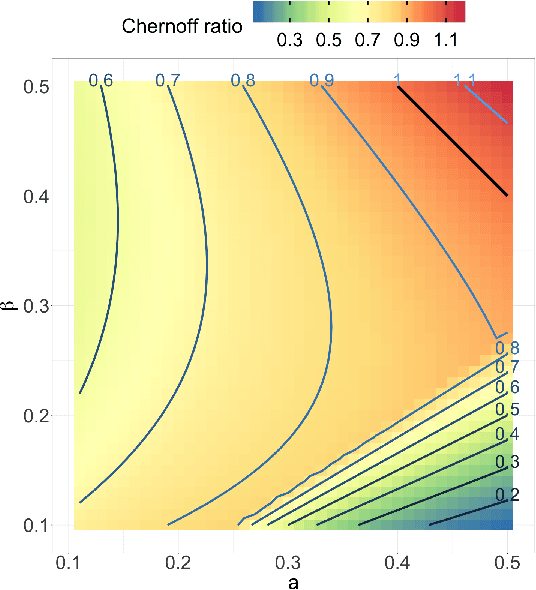
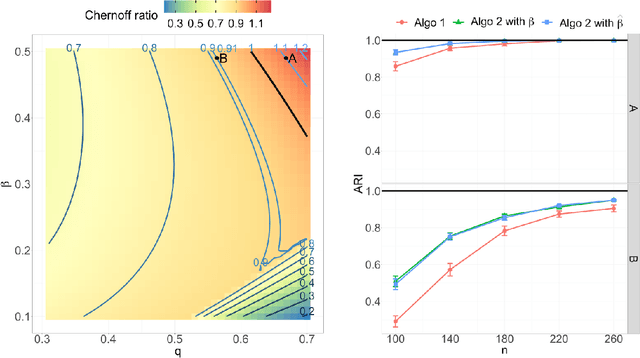
Both observed and unobserved vertex heterogeneity can influence block structure in graphs. To assess these effects on block recovery, we present a comparative analysis of two model-based spectral algorithms for clustering vertices in stochastic blockmodel graphs with vertex covariates. The first algorithm directly estimates the induced block assignments by investigating the estimated block connectivity probability matrix including the vertex covariate effect. The second algorithm estimates the vertex covariate effect and then estimates the induced block assignments after accounting for this effect. We employ Chernoff information to analytically compare the algorithms' performance and derive the Chernoff ratio formula for some special models of interest. Analytic results and simulations suggest that, in general, the second algorithm is preferred: we can better estimate the induced block assignments by first estimating the vertex covariate effect. In addition, real data experiments on a diffusion MRI connectome data set indicate that the second algorithm has the advantages of revealing underlying block structure and taking observed vertex heterogeneity into account in real applications. Our findings emphasize the importance of distinguishing between observed and unobserved factors that can affect block structure in graphs.

Spectral inference for large Stochastic Blockmodels with nodal covariates

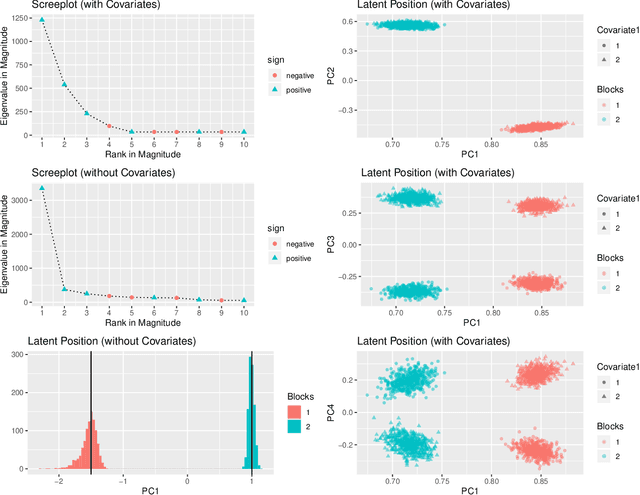
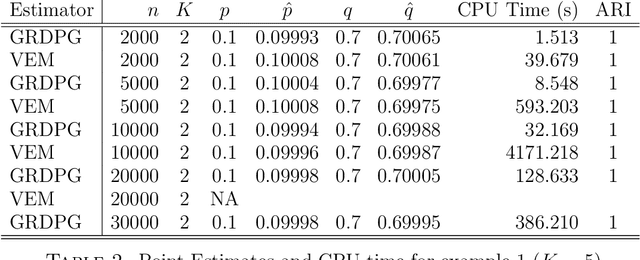
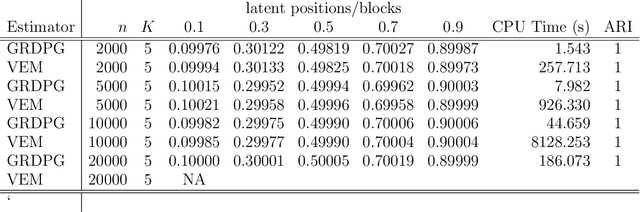
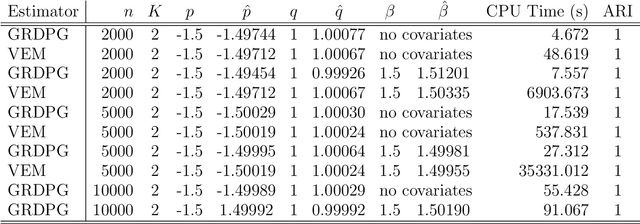
In many applications of network analysis, it is important to distinguish between observed and unobserved factors affecting network structure. To this end, we develop spectral estimators for both unobserved blocks and the effect of covariates in stochastic blockmodels. Our main strategy is to reformulate the stochastic blockmodel estimation problem as recovery of latent positions in a generalized random dot product graph. On the theoretical side, we establish asymptotic normality of our estimators for the subsequent purpose of performing inference. On the applied side, we show that computing our estimator is much faster than standard variational expectation--maximization algorithms and scales well for large networks. The results in this paper provide a foundation to estimate the effect of observed covariates as well as unobserved latent community structure on the probability of link formation in networks.