Particle-Based Score Estimation for State Space Model Learning in Autonomous Driving

Multi-object state estimation is a fundamental problem for robotic applications where a robot must interact with other moving objects. Typically, other objects' relevant state features are not directly observable, and must instead be inferred from observations. Particle filtering can perform such inference given approximate transition and observation models. However, these models are often unknown a priori, yielding a difficult parameter estimation problem since observations jointly carry transition and observation noise. In this work, we consider learning maximum-likelihood parameters using particle methods. Recent methods addressing this problem typically differentiate through time in a particle filter, which requires workarounds to the non-differentiable resampling step, that yield biased or high variance gradient estimates. By contrast, we exploit Fisher's identity to obtain a particle-based approximation of the score function (the gradient of the log likelihood) that yields a low variance estimate while only requiring stepwise differentiation through the transition and observation models. We apply our method to real data collected from autonomous vehicles (AVs) and show that it learns better models than existing techniques and is more stable in training, yielding an effective smoother for tracking the trajectories of vehicles around an AV.

From Denoising Diffusions to Denoising Markov Models

Denoising diffusions are state-of-the-art generative models which exhibit remarkable empirical performance and come with theoretical guarantees. The core idea of these models is to progressively transform the empirical data distribution into a simple Gaussian distribution by adding noise using a diffusion. We obtain new samples whose distribution is close to the data distribution by simulating a "denoising" diffusion approximating the time reversal of this "noising" diffusion. This denoising diffusion relies on approximations of the logarithmic derivatives of the noised data densities, known as scores, obtained using score matching. Such models can be easily extended to perform approximate posterior simulation in high-dimensional scenarios where one can only sample from the prior and simulate synthetic observations from the likelihood. These methods have been primarily developed for data on $\mathbb{R}^d$ while extensions to more general spaces have been developed on a case-by-case basis. We propose here a general framework which not only unifies and generalizes this approach to a wide class of spaces but also leads to an original extension of score matching. We illustrate the resulting class of denoising Markov models on various applications.

Maximum Likelihood Learning of Energy-Based Models for Simulation-Based Inference

We introduce two synthetic likelihood methods for Simulation-Based Inference (SBI), to conduct either amortized or targeted inference from experimental observations when a high-fidelity simulator is available. Both methods learn a conditional energy-based model (EBM) of the likelihood using synthetic data generated by the simulator, conditioned on parameters drawn from a proposal distribution. The learned likelihood can then be combined with any prior to obtain a posterior estimate, from which samples can be drawn using MCMC. Our methods uniquely combine a flexible Energy-Based Model and the minimization of a KL loss: this is in contrast to other synthetic likelihood methods, which either rely on normalizing flows, or minimize score-based objectives; choices that come with known pitfalls. Our first method, Amortized Unnormalized Neural Likelihood Estimation (AUNLE), introduces a tilting trick during training that allows to significantly lower the computational cost of inference by enabling the use of efficient MCMC techniques. Our second method, Sequential UNLE (SUNLE), employs a robust doubly intractable approach in order to re-use simulation data and improve posterior accuracy on a specific dataset. We demonstrate the properties of both methods on a range of synthetic datasets, and apply them to a neuroscience model of the pyloric network in the crab Cancer Borealis, matching the performance of other synthetic likelihood methods at a fraction of the simulation budget.

Categorical SDEs with Simplex Diffusion

Diffusion models typically operate in the standard framework of generative modelling by producing continuously-valued datapoints. To this end, they rely on a progressive Gaussian smoothing of the original data distribution, which admits an SDE interpretation involving increments of a standard Brownian motion. However, some applications such as text generation or reinforcement learning might naturally be better served by diffusing categorical-valued data, i.e., lifting the diffusion to a space of probability distributions. To this end, this short theoretical note proposes Simplex Diffusion, a means to directly diffuse datapoints located on an n-dimensional probability simplex. We show how this relates to the Dirichlet distribution on the simplex and how the analogous SDE is realized thanks to a multi-dimensional Cox-Ingersoll-Ross process (abbreviated as CIR), previously used in economics and mathematical finance. Finally, we make remarks as to the numerical implementation of trajectories of the CIR process, and discuss some limitations of our approach.

Alpha-divergence Variational Inference Meets Importance Weighted Auto-Encoders: Methodology and Asymptotics

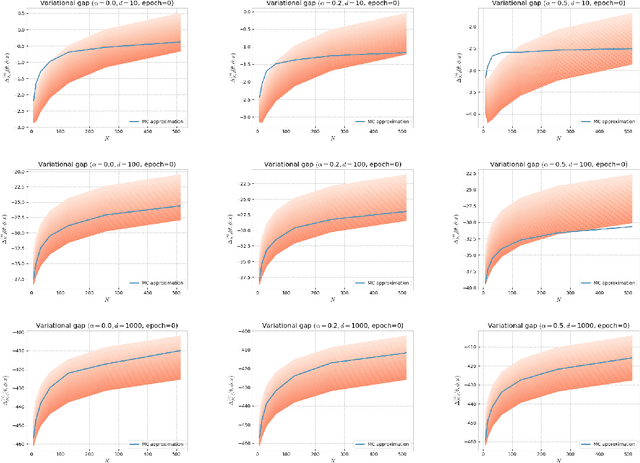
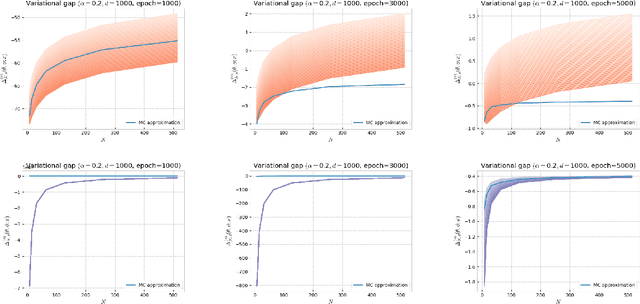
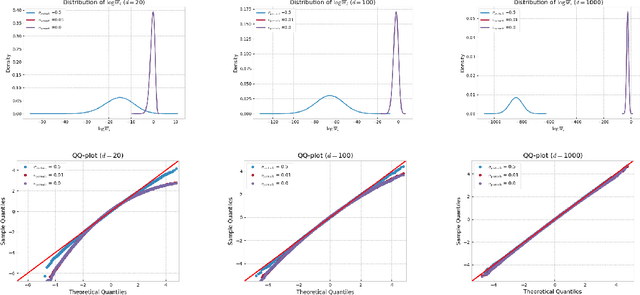
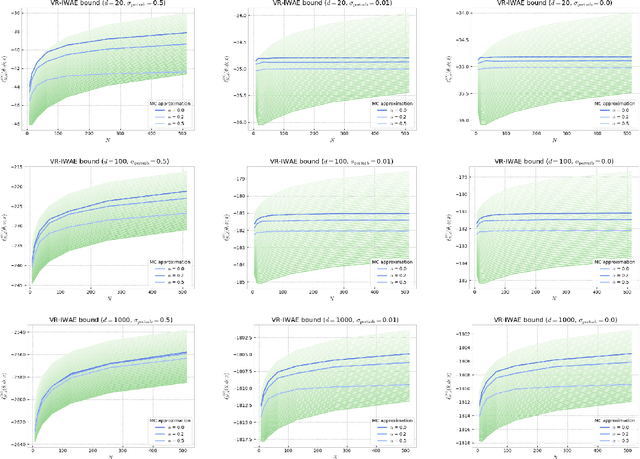
Several algorithms involving the Variational R\'enyi (VR) bound have been proposed to minimize an alpha-divergence between a target posterior distribution and a variational distribution. Despite promising empirical results, those algorithms resort to biased stochastic gradient descent procedures and thus lack theoretical guarantees. In this paper, we formalize and study the VR-IWAE bound, a generalization of the Importance Weighted Auto-Encoder (IWAE) bound. We show that the VR-IWAE bound enjoys several desirable properties and notably leads to the same stochastic gradient descent procedure as the VR bound in the reparameterized case, but this time by relying on unbiased gradient estimators. We then provide two complementary theoretical analyses of the VR-IWAE bound and thus of the standard IWAE bound. Those analyses shed light on the benefits or lack thereof of these bounds. Lastly, we illustrate our theoretical claims over toy and real-data examples.

Spectral Diffusion Processes

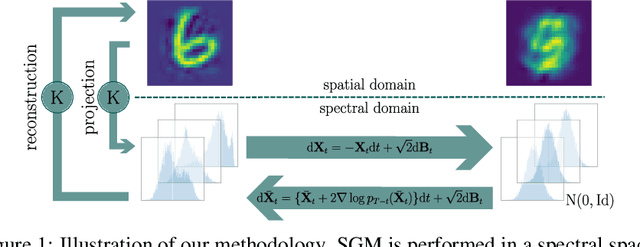
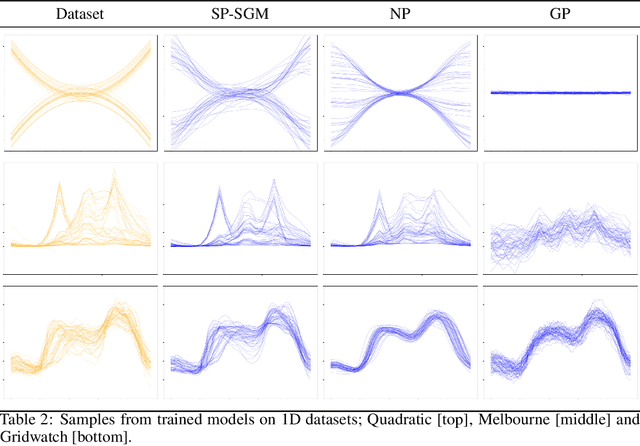
Score-based generative modelling (SGM) has proven to be a very effective method for modelling densities on finite-dimensional spaces. In this work we propose to extend this methodology to learn generative models over functional spaces. To do so, we represent functional data in spectral space to dissociate the stochastic part of the processes from their space-time part. Using dimensionality reduction techniques we then sample from their stochastic component using finite dimensional SGM. We demonstrate our method's effectiveness for modelling various multimodal datasets.

A PAC-Bayes bound for deterministic classifiers

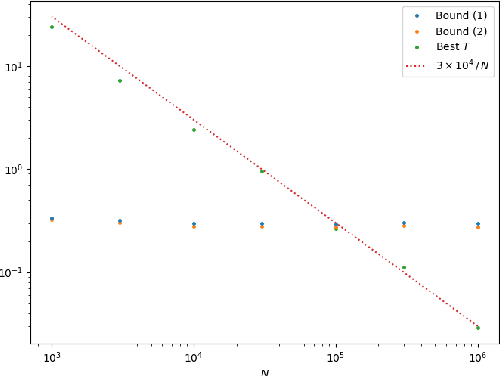
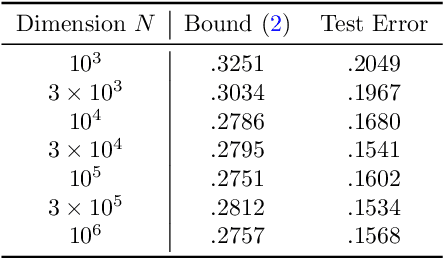
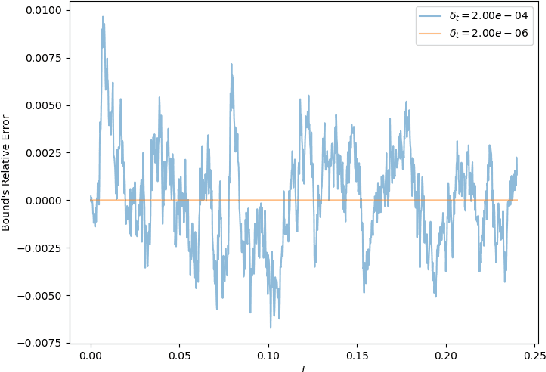
We establish a disintegrated PAC-Bayesian bound, for classifiers that are trained via continuous-time (non-stochastic) gradient descent. Contrarily to what is standard in the PAC-Bayesian setting, our result applies to a training algorithm that is deterministic, conditioned on a random initialisation, without requiring any $\textit{de-randomisation}$ step. We provide a broad discussion of the main features of the bound that we propose, and we study analytically and empirically its behaviour on linear models, finding promising results.

Score-Based Diffusion meets Annealed Importance Sampling

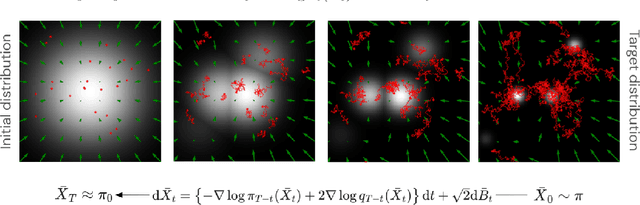
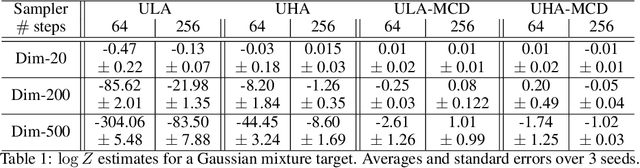
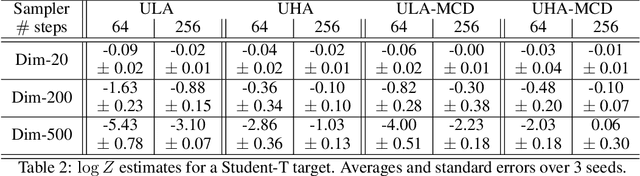
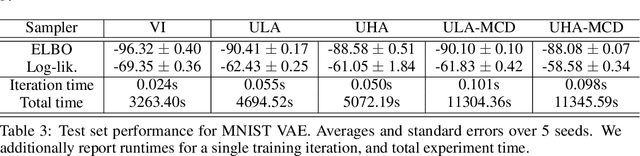
More than twenty years after its introduction, Annealed Importance Sampling (AIS) remains one of the most effective methods for marginal likelihood estimation. It relies on a sequence of distributions interpolating between a tractable initial distribution and the target distribution of interest which we simulate from approximately using a non-homogeneous Markov chain. To obtain an importance sampling estimate of the marginal likelihood, AIS introduces an extended target distribution to reweight the Markov chain proposal. While much effort has been devoted to improving the proposal distribution used by AIS, by changing the intermediate distributions and corresponding Markov kernels, an underappreciated issue is that AIS uses a convenient but suboptimal extended target distribution. This can hinder its performance. We here leverage recent progress in score-based generative modeling (SGM) to approximate the optimal extended target distribution for AIS proposals corresponding to the discretization of Langevin and Hamiltonian dynamics. We demonstrate these novel, differentiable, AIS procedures on a number of synthetic benchmark distributions and variational auto-encoders.

An Empirical Study of Implicit Regularization in Deep Offline RL

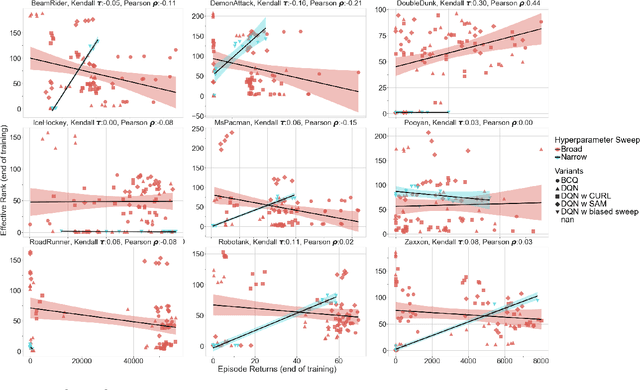
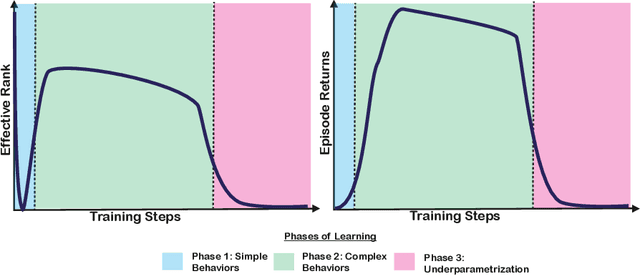
Deep neural networks are the most commonly used function approximators in offline reinforcement learning. Prior works have shown that neural nets trained with TD-learning and gradient descent can exhibit implicit regularization that can be characterized by under-parameterization of these networks. Specifically, the rank of the penultimate feature layer, also called \textit{effective rank}, has been observed to drastically collapse during the training. In turn, this collapse has been argued to reduce the model's ability to further adapt in later stages of learning, leading to the diminished final performance. Such an association between the effective rank and performance makes effective rank compelling for offline RL, primarily for offline policy evaluation. In this work, we conduct a careful empirical study on the relation between effective rank and performance on three offline RL datasets : bsuite, Atari, and DeepMind lab. We observe that a direct association exists only in restricted settings and disappears in the more extensive hyperparameter sweeps. Also, we empirically identify three phases of learning that explain the impact of implicit regularization on the learning dynamics and found that bootstrapping alone is insufficient to explain the collapse of the effective rank. Further, we show that several other factors could confound the relationship between effective rank and performance and conclude that studying this association under simplistic assumptions could be highly misleading.

Riemannian Diffusion Schrödinger Bridge

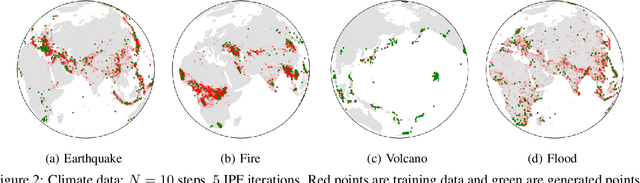
Score-based generative models exhibit state of the art performance on density estimation and generative modeling tasks. These models typically assume that the data geometry is flat, yet recent extensions have been developed to synthesize data living on Riemannian manifolds. Existing methods to accelerate sampling of diffusion models are typically not applicable in the Riemannian setting and Riemannian score-based methods have not yet been adapted to the important task of interpolation of datasets. To overcome these issues, we introduce \emph{Riemannian Diffusion Schr\"odinger Bridge}. Our proposed method generalizes Diffusion Schr\"odinger Bridge introduced in \cite{debortoli2021neurips} to the non-Euclidean setting and extends Riemannian score-based models beyond the first time reversal. We validate our proposed method on synthetic data and real Earth and climate data.