Learning with Importance Weighted Variational Inference: Asymptotics for Gradient Estimators of the VR-IWAE Bound

Several popular variational bounds involving importance weighting ideas have been proposed to generalize and improve on the Evidence Lower BOund (ELBO) in the context of maximum likelihood optimization, such as the Importance Weighted Auto-Encoder (IWAE) and the Variational R\'enyi (VR) bounds. The methodology to learn the parameters of interest using these bounds typically amounts to running gradient-based variational inference algorithms that incorporate the reparameterization trick. However, the way the choice of the variational bound impacts the outcome of variational inference algorithms can be unclear. Recently, the VR-IWAE bound was introduced as a variational bound that unifies the ELBO, IWAE and VR bounds methodologies. In this paper, we provide two analyses for the reparameterized and doubly-reparameterized gradient estimators of the VR-IWAE bound, which reveal the advantages and limitations of these gradient estimators while enabling us to compare of the ELBO, IWAE and VR bounds methodologies. Our work advances the understanding of importance weighted variational inference methods and we illustrate our theoretical findings empirically.

Alpha-divergence Variational Inference Meets Importance Weighted Auto-Encoders: Methodology and Asymptotics

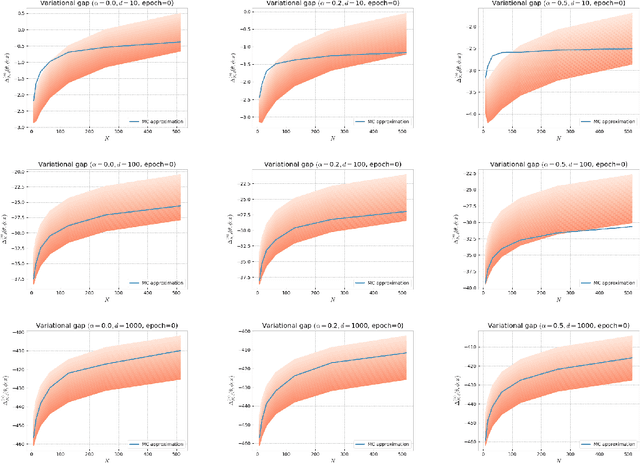
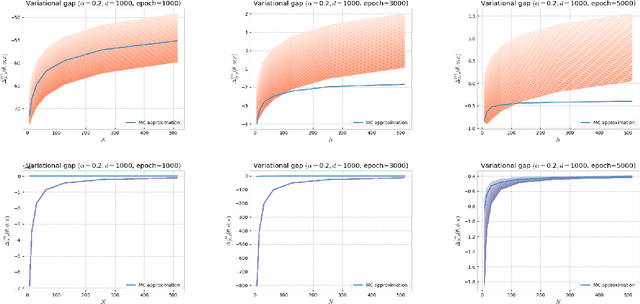
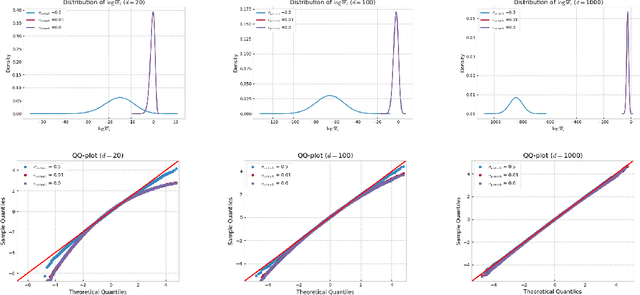
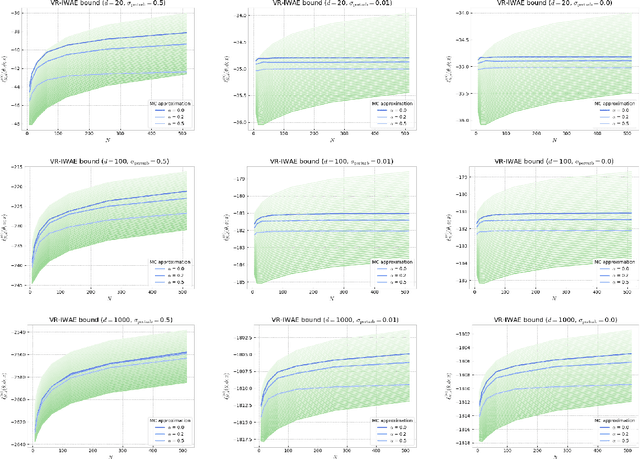
Several algorithms involving the Variational R\'enyi (VR) bound have been proposed to minimize an alpha-divergence between a target posterior distribution and a variational distribution. Despite promising empirical results, those algorithms resort to biased stochastic gradient descent procedures and thus lack theoretical guarantees. In this paper, we formalize and study the VR-IWAE bound, a generalization of the Importance Weighted Auto-Encoder (IWAE) bound. We show that the VR-IWAE bound enjoys several desirable properties and notably leads to the same stochastic gradient descent procedure as the VR bound in the reparameterized case, but this time by relying on unbiased gradient estimators. We then provide two complementary theoretical analyses of the VR-IWAE bound and thus of the standard IWAE bound. Those analyses shed light on the benefits or lack thereof of these bounds. Lastly, we illustrate our theoretical claims over toy and real-data examples.

Mixture weights optimisation for Alpha-Divergence Variational Inference

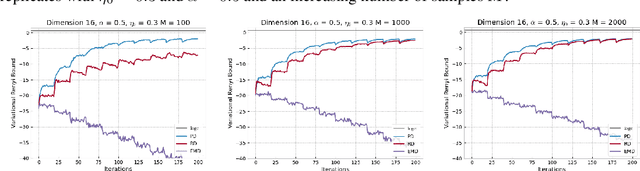
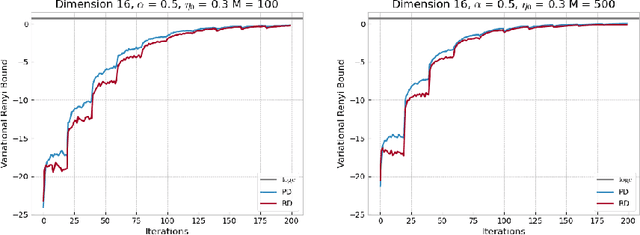
This paper focuses on $\alpha$-divergence minimisation methods for Variational Inference. More precisely, we are interested in algorithms optimising the mixture weights of any given mixture model, without any information on the underlying distribution of its mixture components parameters. The Power Descent, defined for all $\alpha \neq 1$, is one such algorithm and we establish in our work the full proof of its convergence towards the optimal mixture weights when $\alpha <1$. Since the $\alpha$-divergence recovers the widely-used forward Kullback-Leibler when $\alpha \to 1$, we then extend the Power Descent to the case $\alpha = 1$ and show that we obtain an Entropic Mirror Descent. This leads us to investigate the link between Power Descent and Entropic Mirror Descent: first-order approximations allow us to introduce the Renyi Descent, a novel algorithm for which we prove an $O(1/N)$ convergence rate. Lastly, we compare numerically the behavior of the unbiased Power Descent and of the biased Renyi Descent and we discuss the potential advantages of one algorithm over the other.

Monotonic Alpha-divergence Minimisation

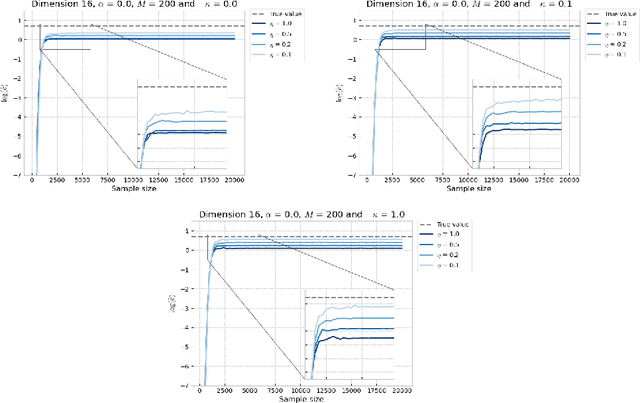
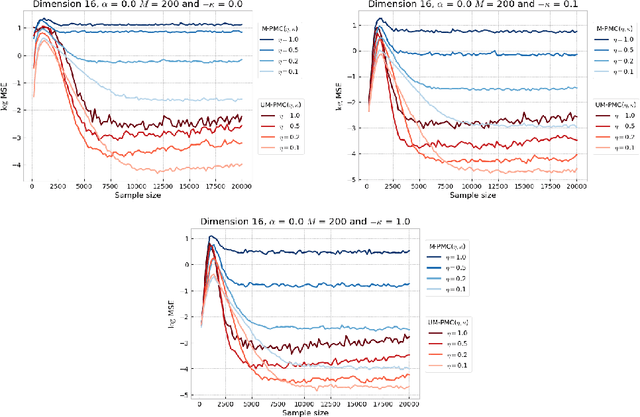
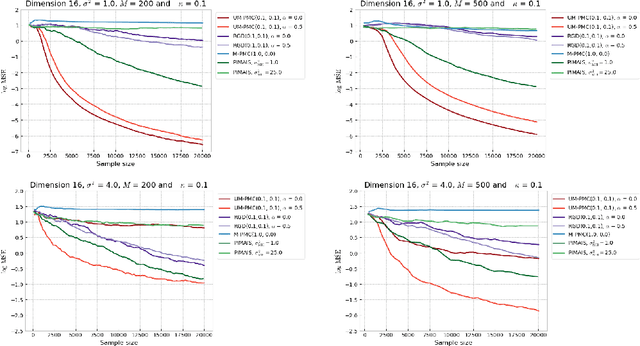
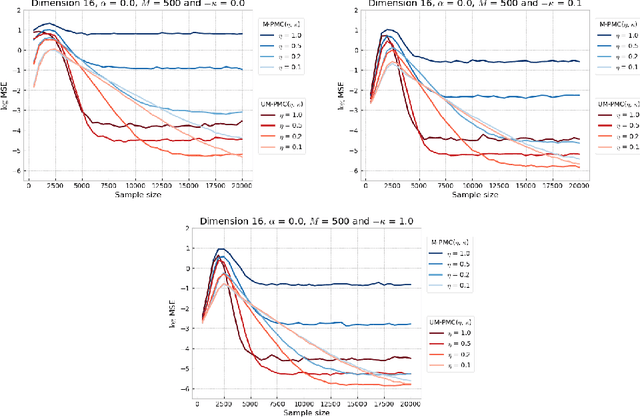
In this paper, we introduce a novel iterative algorithm which carries out $\alpha$-divergence minimisation by ensuring a systematic decrease in the $\alpha$-divergence at each step. In its most general form, our framework allows us to simultaneously optimise the weights and components parameters of a given mixture model. Notably, our approach permits to build on various methods previously proposed for $\alpha$-divergence minimisation such as gradient or power descent schemes. Furthermore, we shed a new light on an integrated Expectation Maximization algorithm. We provide empirical evidence that our methodology yields improved results, all the while illustrating the numerical benefits of having introduced some flexibility through the parameter $\alpha$ of the $\alpha$-divergence.