Ankit Singh Rawat
Supervision Complexity and its Role in Knowledge Distillation
Jan 28, 2023Abstract:Despite the popularity and efficacy of knowledge distillation, there is limited understanding of why it helps. In order to study the generalization behavior of a distilled student, we propose a new theoretical framework that leverages supervision complexity: a measure of alignment between teacher-provided supervision and the student's neural tangent kernel. The framework highlights a delicate interplay among the teacher's accuracy, the student's margin with respect to the teacher predictions, and the complexity of the teacher predictions. Specifically, it provides a rigorous justification for the utility of various techniques that are prevalent in the context of distillation, such as early stopping and temperature scaling. Our analysis further suggests the use of online distillation, where a student receives increasingly more complex supervision from teachers in different stages of their training. We demonstrate efficacy of online distillation and validate the theoretical findings on a range of image classification benchmarks and model architectures.
EmbedDistill: A Geometric Knowledge Distillation for Information Retrieval
Jan 27, 2023



Abstract:Large neural models (such as Transformers) achieve state-of-the-art performance for information retrieval (IR). In this paper, we aim to improve distillation methods that pave the way for the deployment of such models in practice. The proposed distillation approach supports both retrieval and re-ranking stages and crucially leverages the relative geometry among queries and documents learned by the large teacher model. It goes beyond existing distillation methods in the IR literature, which simply rely on the teacher's scalar scores over the training data, on two fronts: providing stronger signals about local geometry via embedding matching and attaining better coverage of data manifold globally via query generation. Embedding matching provides a stronger signal to align the representations of the teacher and student models. At the same time, query generation explores the data manifold to reduce the discrepancies between the student and teacher where training data is sparse. Our distillation approach is theoretically justified and applies to both dual encoder (DE) and cross-encoder (CE) models. Furthermore, for distilling a CE model to a DE model via embedding matching, we propose a novel dual pooling-based scorer for the CE model that facilitates a distillation-friendly embedding geometry, especially for DE student models.
Large Language Models with Controllable Working Memory
Nov 09, 2022



Abstract:Large language models (LLMs) have led to a series of breakthroughs in natural language processing (NLP), owing to their excellent understanding and generation abilities. Remarkably, what further sets these models apart is the massive amounts of world knowledge they internalize during pretraining. While many downstream applications provide the model with an informational context to aid its performance on the underlying task, how the model's world knowledge interacts with the factual information presented in the context remains under explored. As a desirable behavior, an LLM should give precedence to the context whenever it contains task-relevant information that conflicts with the model's memorized knowledge. This enables model predictions to be grounded in the context, which can then be used to update or correct specific model predictions without frequent retraining. By contrast, when the context is irrelevant to the task, the model should ignore it and fall back on its internal knowledge. In this paper, we undertake a first joint study of the aforementioned two properties, namely controllability and robustness, in the context of LLMs. We demonstrate that state-of-the-art T5 and PaLM (both pretrained and finetuned) could exhibit poor controllability and robustness, which do not scale with increasing model size. As a solution, we propose a novel method - Knowledge Aware FineTuning (KAFT) - to strengthen both controllability and robustness by incorporating counterfactual and irrelevant contexts to standard supervised datasets. Our comprehensive evaluation showcases the utility of KAFT across model architectures and sizes.
Large Models are Parsimonious Learners: Activation Sparsity in Trained Transformers
Oct 12, 2022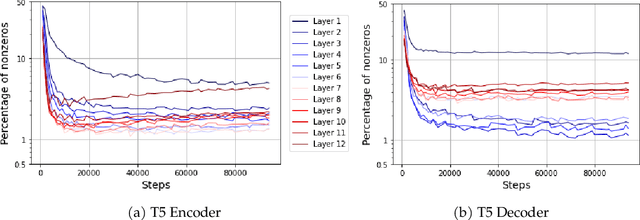

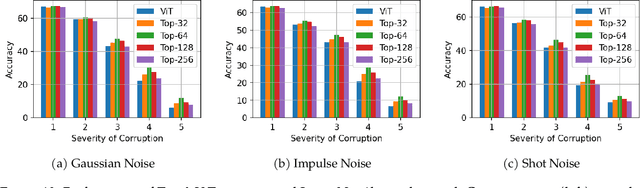
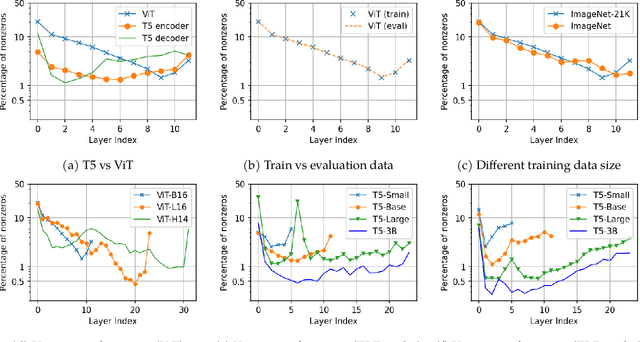
Abstract:This paper studies the curious phenomenon for machine learning models with Transformer architectures that their activation maps are sparse. By activation map we refer to the intermediate output of the multi-layer perceptrons (MLPs) after a ReLU activation function, and by "sparse" we mean that on average very few entries (e.g., 3.0% for T5-Base and 6.3% for ViT-B16) are nonzero for each input to MLP. Moreover, larger Transformers with more layers and wider MLP hidden dimensions are sparser as measured by the percentage of nonzero entries. Through extensive experiments we demonstrate that the emergence of sparsity is a prevalent phenomenon that occurs for both natural language processing and vision tasks, on both training and evaluation data, for Transformers of various configurations, at layers of all depth levels, as well as for other architectures including MLP-mixers and 2-layer MLPs. We show that sparsity also emerges using training datasets with random labels, or with random inputs, or with infinite amount of data, demonstrating that sparsity is not a result of a specific family of datasets. We discuss how sparsity immediately implies a way to significantly reduce the FLOP count and improve efficiency for Transformers. Moreover, we demonstrate perhaps surprisingly that enforcing an even sparser activation via Top-k thresholding with a small value of k brings a collection of desired but missing properties for Transformers, namely less sensitivity to noisy training data, more robustness to input corruptions, and better calibration for their prediction confidence.
A Fourier Approach to Mixture Learning
Oct 06, 2022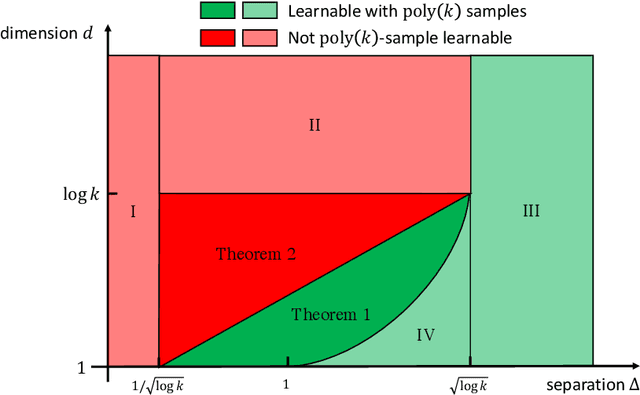

Abstract:We revisit the problem of learning mixtures of spherical Gaussians. Given samples from mixture $\frac{1}{k}\sum_{j=1}^{k}\mathcal{N}(\mu_j, I_d)$, the goal is to estimate the means $\mu_1, \mu_2, \ldots, \mu_k \in \mathbb{R}^d$ up to a small error. The hardness of this learning problem can be measured by the separation $\Delta$ defined as the minimum distance between all pairs of means. Regev and Vijayaraghavan (2017) showed that with $\Delta = \Omega(\sqrt{\log k})$ separation, the means can be learned using $\mathrm{poly}(k, d)$ samples, whereas super-polynomially many samples are required if $\Delta = o(\sqrt{\log k})$ and $d = \Omega(\log k)$. This leaves open the low-dimensional regime where $d = o(\log k)$. In this work, we give an algorithm that efficiently learns the means in $d = O(\log k/\log\log k)$ dimensions under separation $d/\sqrt{\log k}$ (modulo doubly logarithmic factors). This separation is strictly smaller than $\sqrt{\log k}$, and is also shown to be necessary. Along with the results of Regev and Vijayaraghavan (2017), our work almost pins down the critical separation threshold at which efficient parameter learning becomes possible for spherical Gaussian mixtures. More generally, our algorithm runs in time $\mathrm{poly}(k)\cdot f(d, \Delta, \epsilon)$, and is thus fixed-parameter tractable in parameters $d$, $\Delta$ and $\epsilon$. Our approach is based on estimating the Fourier transform of the mixture at carefully chosen frequencies, and both the algorithm and its analysis are simple and elementary. Our positive results can be easily extended to learning mixtures of non-Gaussian distributions, under a mild condition on the Fourier spectrum of the distribution.
Generalization Properties of Retrieval-based Models
Oct 06, 2022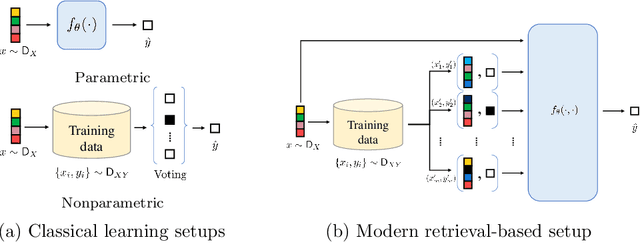
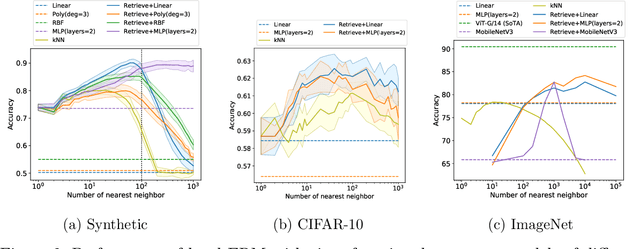
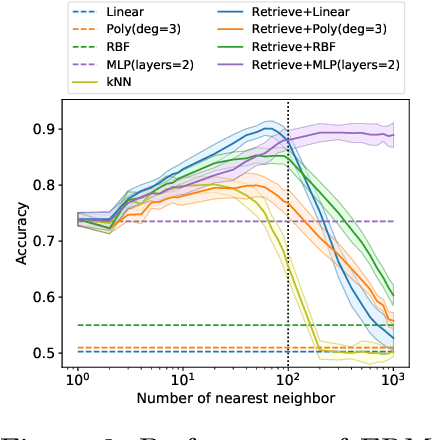
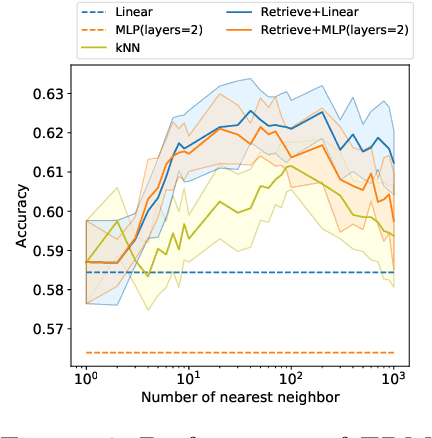
Abstract:Many modern high-performing machine learning models such as GPT-3 primarily rely on scaling up models, e.g., transformer networks. Simultaneously, a parallel line of work aims to improve the model performance by augmenting an input instance with other (labeled) instances during inference. Examples of such augmentations include task-specific prompts and similar examples retrieved from the training data by a nonparametric component. Remarkably, retrieval-based methods have enjoyed success on a wide range of problems, ranging from standard natural language processing and vision tasks to protein folding, as demonstrated by many recent efforts, including WebGPT and AlphaFold. Despite growing literature showcasing the promise of these models, the theoretical underpinning for such models remains underexplored. In this paper, we present a formal treatment of retrieval-based models to characterize their generalization ability. In particular, we focus on two classes of retrieval-based classification approaches: First, we analyze a local learning framework that employs an explicit local empirical risk minimization based on retrieved examples for each input instance. Interestingly, we show that breaking down the underlying learning task into local sub-tasks enables the model to employ a low complexity parametric component to ensure good overall accuracy. The second class of retrieval-based approaches we explore learns a global model using kernel methods to directly map an input instance and retrieved examples to a prediction, without explicitly solving a local learning task.
Teacher Guided Training: An Efficient Framework for Knowledge Transfer
Aug 14, 2022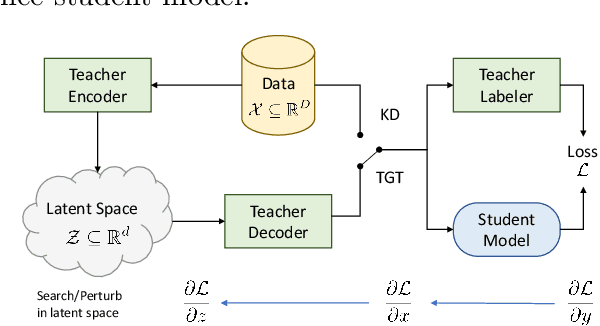
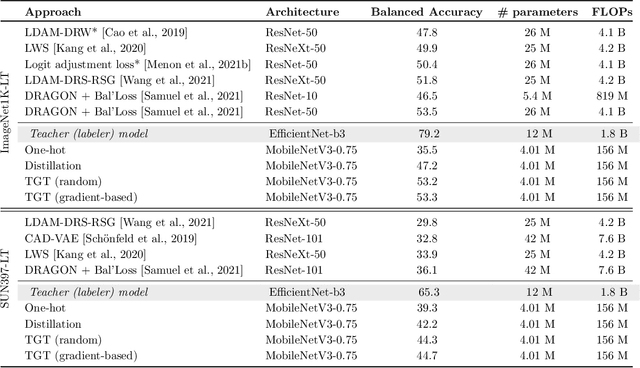
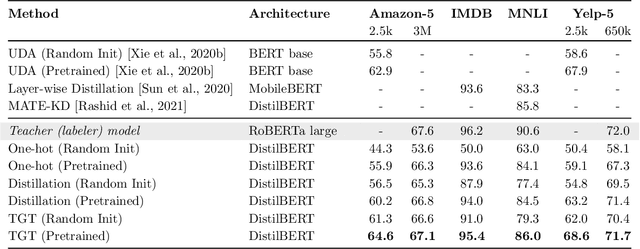
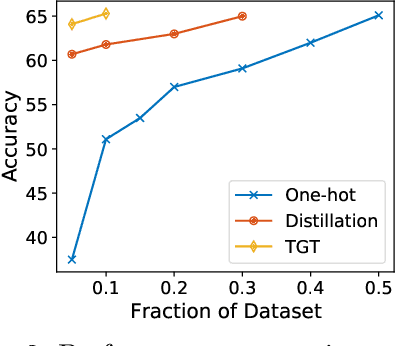
Abstract:The remarkable performance gains realized by large pretrained models, e.g., GPT-3, hinge on the massive amounts of data they are exposed to during training. Analogously, distilling such large models to compact models for efficient deployment also necessitates a large amount of (labeled or unlabeled) training data. In this paper, we propose the teacher-guided training (TGT) framework for training a high-quality compact model that leverages the knowledge acquired by pretrained generative models, while obviating the need to go through a large volume of data. TGT exploits the fact that the teacher has acquired a good representation of the underlying data domain, which typically corresponds to a much lower dimensional manifold than the input space. Furthermore, we can use the teacher to explore input space more efficiently through sampling or gradient-based methods; thus, making TGT especially attractive for limited data or long-tail settings. We formally capture this benefit of proposed data-domain exploration in our generalization bounds. We find that TGT can improve accuracy on several image classification benchmarks as well as a range of text classification and retrieval tasks.
ELM: Embedding and Logit Margins for Long-Tail Learning
Apr 27, 2022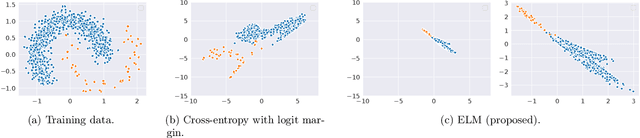
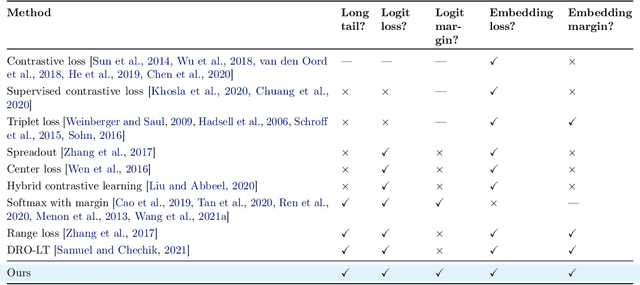
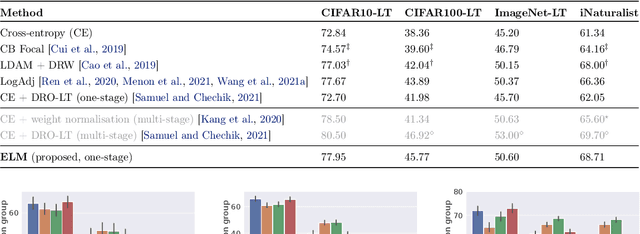
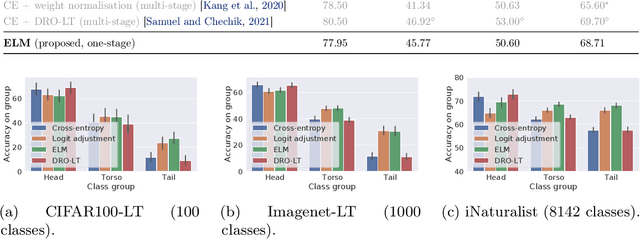
Abstract:Long-tail learning is the problem of learning under skewed label distributions, which pose a challenge for standard learners. Several recent approaches for the problem have proposed enforcing a suitable margin in logit space. Such techniques are intuitive analogues of the guiding principle behind SVMs, and are equally applicable to linear models and neural models. However, when applied to neural models, such techniques do not explicitly control the geometry of the learned embeddings. This can be potentially sub-optimal, since embeddings for tail classes may be diffuse, resulting in poor generalization for these classes. We present Embedding and Logit Margins (ELM), a unified approach to enforce margins in logit space, and regularize the distribution of embeddings. This connects losses for long-tail learning to proposals in the literature on metric embedding, and contrastive learning. We theoretically show that minimising the proposed ELM objective helps reduce the generalisation gap. The ELM method is shown to perform well empirically, and results in tighter tail class embeddings.
FedLite: A Scalable Approach for Federated Learning on Resource-constrained Clients
Feb 16, 2022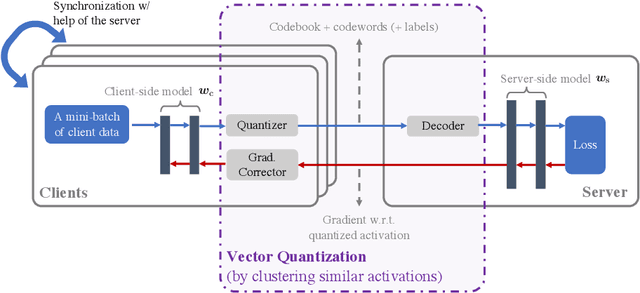

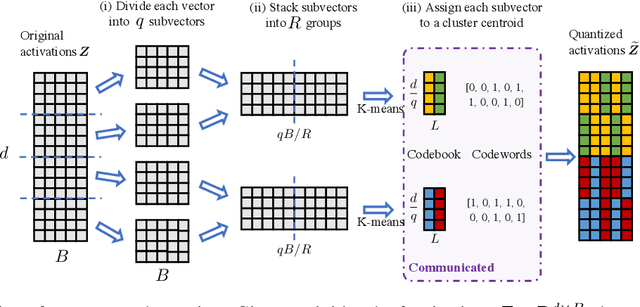
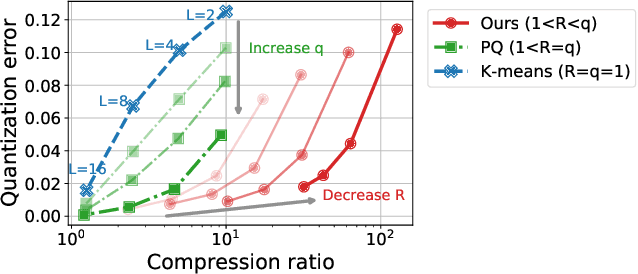
Abstract:In classical federated learning, the clients contribute to the overall training by communicating local updates for the underlying model on their private data to a coordinating server. However, updating and communicating the entire model becomes prohibitively expensive when resource-constrained clients collectively aim to train a large machine learning model. Split learning provides a natural solution in such a setting, where only a small part of the model is stored and trained on clients while the remaining large part of the model only stays at the servers. However, the model partitioning employed in split learning introduces a significant amount of communication cost. This paper addresses this issue by compressing the additional communication using a novel clustering scheme accompanied by a gradient correction method. Extensive empirical evaluations on image and text benchmarks show that the proposed method can achieve up to $490\times$ communication cost reduction with minimal drop in accuracy, and enables a desirable performance vs. communication trade-off.
When in Doubt, Summon the Titans: Efficient Inference with Large Models
Oct 19, 2021
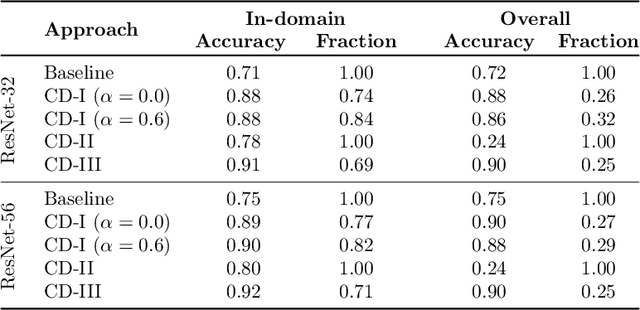
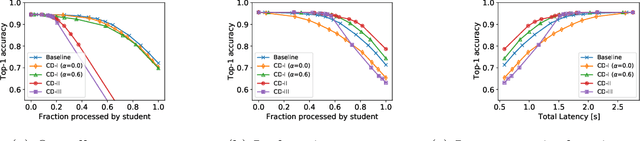
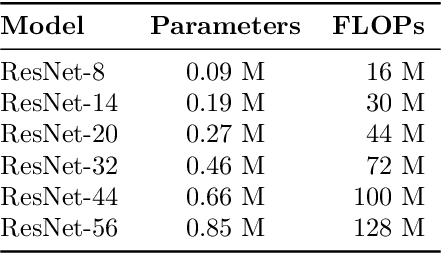
Abstract:Scaling neural networks to "large" sizes, with billions of parameters, has been shown to yield impressive results on many challenging problems. However, the inference cost incurred by such large models often prevents their application in most real-world settings. In this paper, we propose a two-stage framework based on distillation that realizes the modelling benefits of the large models, while largely preserving the computational benefits of inference with more lightweight models. In a nutshell, we use the large teacher models to guide the lightweight student models to only make correct predictions on a subset of "easy" examples; for the "hard" examples, we fall-back to the teacher. Such an approach allows us to efficiently employ large models in practical scenarios where easy examples are much more frequent than rare hard examples. Our proposed use of distillation to only handle easy instances allows for a more aggressive trade-off in the student size, thereby reducing the amortized cost of inference and achieving better accuracy than standard distillation. Empirically, we demonstrate the benefits of our approach on both image classification and natural language processing benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge