A Fourier Approach to Mixture Learning
Paper and Code
Oct 06, 2022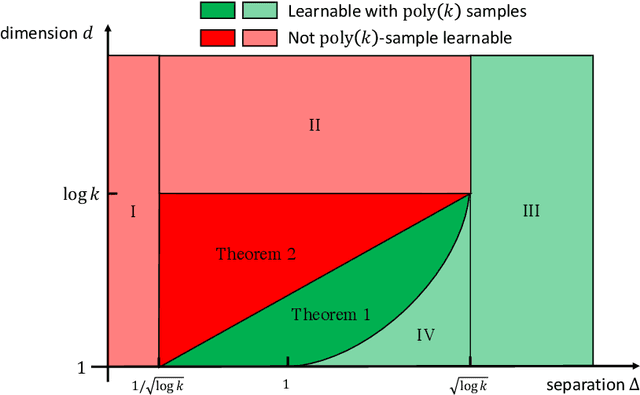

We revisit the problem of learning mixtures of spherical Gaussians. Given samples from mixture $\frac{1}{k}\sum_{j=1}^{k}\mathcal{N}(\mu_j, I_d)$, the goal is to estimate the means $\mu_1, \mu_2, \ldots, \mu_k \in \mathbb{R}^d$ up to a small error. The hardness of this learning problem can be measured by the separation $\Delta$ defined as the minimum distance between all pairs of means. Regev and Vijayaraghavan (2017) showed that with $\Delta = \Omega(\sqrt{\log k})$ separation, the means can be learned using $\mathrm{poly}(k, d)$ samples, whereas super-polynomially many samples are required if $\Delta = o(\sqrt{\log k})$ and $d = \Omega(\log k)$. This leaves open the low-dimensional regime where $d = o(\log k)$. In this work, we give an algorithm that efficiently learns the means in $d = O(\log k/\log\log k)$ dimensions under separation $d/\sqrt{\log k}$ (modulo doubly logarithmic factors). This separation is strictly smaller than $\sqrt{\log k}$, and is also shown to be necessary. Along with the results of Regev and Vijayaraghavan (2017), our work almost pins down the critical separation threshold at which efficient parameter learning becomes possible for spherical Gaussian mixtures. More generally, our algorithm runs in time $\mathrm{poly}(k)\cdot f(d, \Delta, \epsilon)$, and is thus fixed-parameter tractable in parameters $d$, $\Delta$ and $\epsilon$. Our approach is based on estimating the Fourier transform of the mixture at carefully chosen frequencies, and both the algorithm and its analysis are simple and elementary. Our positive results can be easily extended to learning mixtures of non-Gaussian distributions, under a mild condition on the Fourier spectrum of the distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge