Open Problem: Approximate Planning of POMDPs in the class of Memoryless Policies

Planning plays an important role in the broad class of decision theory. Planning has drawn much attention in recent work in the robotics and sequential decision making areas. Recently, Reinforcement Learning (RL), as an agent-environment interaction problem, has brought further attention to planning methods. Generally in RL, one can assume a generative model, e.g. graphical models, for the environment, and then the task for the RL agent is to learn the model parameters and find the optimal strategy based on these learnt parameters. Based on environment behavior, the agent can assume various types of generative models, e.g. Multi Armed Bandit for a static environment, or Markov Decision Process (MDP) for a dynamic environment. The advantage of these popular models is their simplicity, which results in tractable methods of learning the parameters and finding the optimal policy. The drawback of these models is again their simplicity: these models usually underfit and underestimate the actual environment behavior. For example, in robotics, the agent usually has noisy observations of the environment inner state and MDP is not a suitable model. More complex models like Partially Observable Markov Decision Process (POMDP) can compensate for this drawback. Fitting this model to the environment, where the partial observation is given to the agent, generally gives dramatic performance improvement, sometimes unbounded improvement, compared to MDP. In general, finding the optimal policy for the POMDP model is computationally intractable and fully non convex, even for the class of memoryless policies. The open problem is to come up with a method to find an exact or an approximate optimal stochastic memoryless policy for POMDP models.

Discovering Neuronal Cell Types and Their Gene Expression Profiles Using a Spatial Point Process Mixture Model

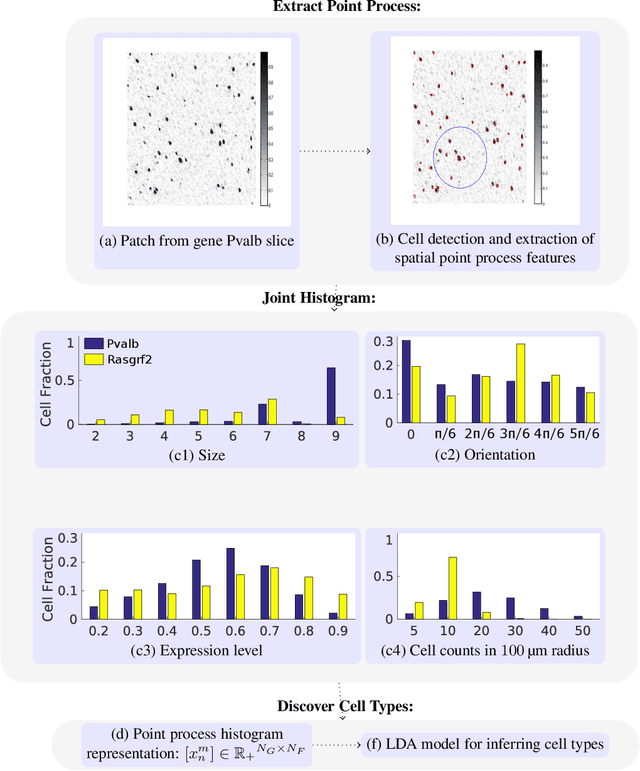
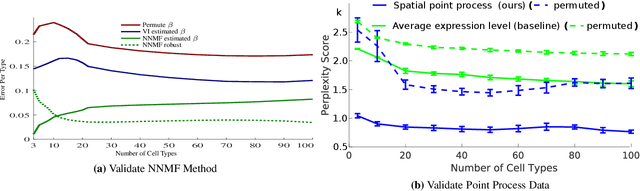
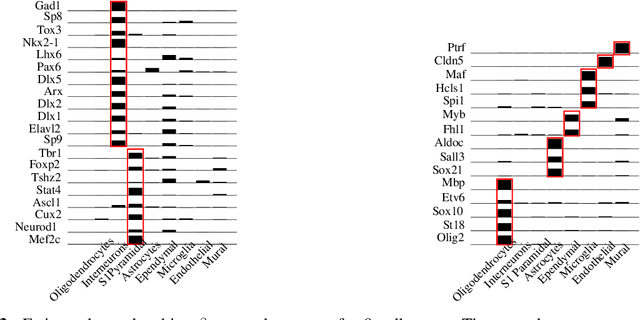
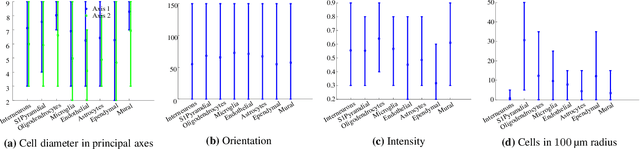
Cataloging the neuronal cell types that comprise circuitry of individual brain regions is a major goal of modern neuroscience and the BRAIN initiative. Single-cell RNA sequencing can now be used to measure the gene expression profiles of individual neurons and to categorize neurons based on their gene expression profiles. While the single-cell techniques are extremely powerful and hold great promise, they are currently still labor intensive, have a high cost per cell, and, most importantly, do not provide information on spatial distribution of cell types in specific regions of the brain. We propose a complementary approach that uses computational methods to infer the cell types and their gene expression profiles through analysis of brain-wide single-cell resolution in situ hybridization (ISH) imagery contained in the Allen Brain Atlas (ABA). We measure the spatial distribution of neurons labeled in the ISH image for each gene and model it as a spatial point process mixture, whose mixture weights are given by the cell types which express that gene. By fitting a point process mixture model jointly to the ISH images, we infer both the spatial point process distribution for each cell type and their gene expression profile. We validate our predictions of cell type-specific gene expression profiles using single cell RNA sequencing data, recently published for the mouse somatosensory cortex. Jointly with the gene expression profiles, cell features such as cell size, orientation, intensity and local density level are inferred per cell type.

Reinforcement Learning of POMDPs using Spectral Methods

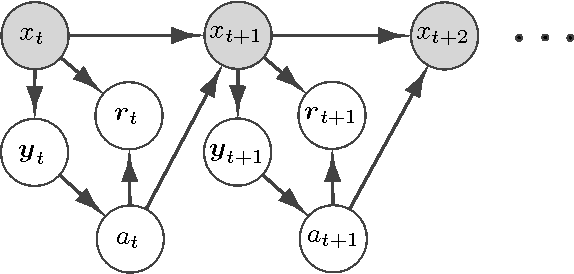
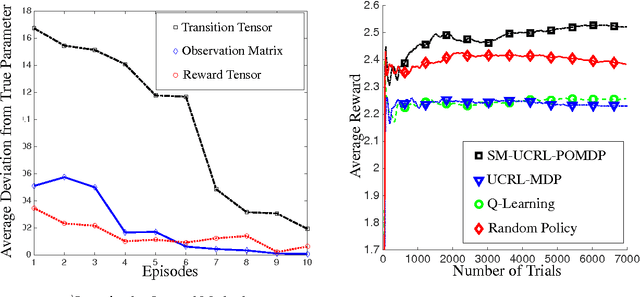
We propose a new reinforcement learning algorithm for partially observable Markov decision processes (POMDP) based on spectral decomposition methods. While spectral methods have been previously employed for consistent learning of (passive) latent variable models such as hidden Markov models, POMDPs are more challenging since the learner interacts with the environment and possibly changes the future observations in the process. We devise a learning algorithm running through episodes, in each episode we employ spectral techniques to learn the POMDP parameters from a trajectory generated by a fixed policy. At the end of the episode, an optimization oracle returns the optimal memoryless planning policy which maximizes the expected reward based on the estimated POMDP model. We prove an order-optimal regret bound with respect to the optimal memoryless policy and efficient scaling with respect to the dimensionality of observation and action spaces.

Tensor vs Matrix Methods: Robust Tensor Decomposition under Block Sparse Perturbations

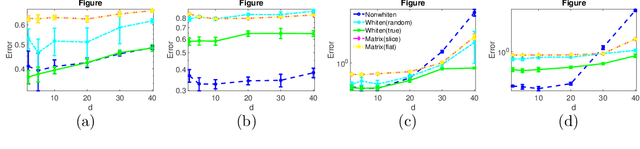
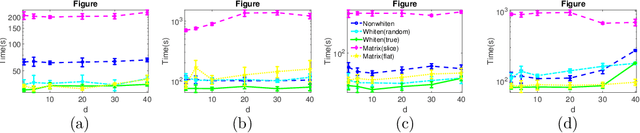
Robust tensor CP decomposition involves decomposing a tensor into low rank and sparse components. We propose a novel non-convex iterative algorithm with guaranteed recovery. It alternates between low-rank CP decomposition through gradient ascent (a variant of the tensor power method), and hard thresholding of the residual. We prove convergence to the globally optimal solution under natural incoherence conditions on the low rank component, and bounded level of sparse perturbations. We compare our method with natural baselines which apply robust matrix PCA either to the {\em flattened} tensor, or to the matrix slices of the tensor. Our method can provably handle a far greater level of perturbation when the sparse tensor is block-structured. This naturally occurs in many applications such as the activity detection task in videos. Our experiments validate these findings. Thus, we establish that tensor methods can tolerate a higher level of gross corruptions compared to matrix methods.

Fast and Guaranteed Tensor Decomposition via Sketching

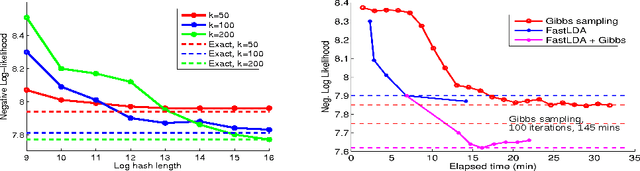
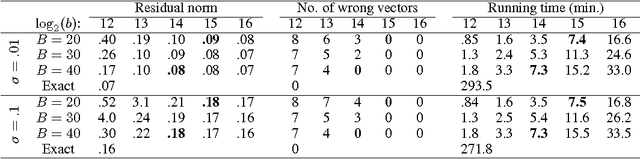
Tensor CANDECOMP/PARAFAC (CP) decomposition has wide applications in statistical learning of latent variable models and in data mining. In this paper, we propose fast and randomized tensor CP decomposition algorithms based on sketching. We build on the idea of count sketches, but introduce many novel ideas which are unique to tensors. We develop novel methods for randomized computation of tensor contractions via FFTs, without explicitly forming the tensors. Such tensor contractions are encountered in decomposition methods such as tensor power iterations and alternating least squares. We also design novel colliding hashes for symmetric tensors to further save time in computing the sketches. We then combine these sketching ideas with existing whitening and tensor power iterative techniques to obtain the fastest algorithm on both sparse and dense tensors. The quality of approximation under our method does not depend on properties such as sparsity, uniformity of elements, etc. We apply the method for topic modeling and obtain competitive results.

Online Tensor Methods for Learning Latent Variable Models

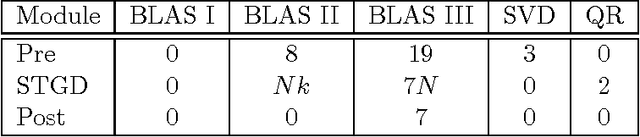
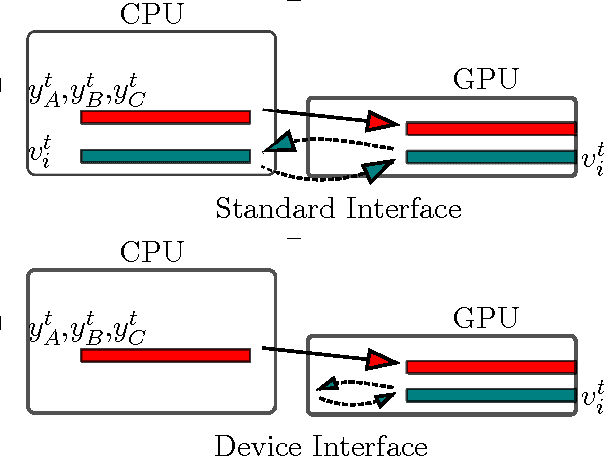
We introduce an online tensor decomposition based approach for two latent variable modeling problems namely, (1) community detection, in which we learn the latent communities that the social actors in social networks belong to, and (2) topic modeling, in which we infer hidden topics of text articles. We consider decomposition of moment tensors using stochastic gradient descent. We conduct optimization of multilinear operations in SGD and avoid directly forming the tensors, to save computational and storage costs. We present optimized algorithm in two platforms. Our GPU-based implementation exploits the parallelism of SIMD architectures to allow for maximum speed-up by a careful optimization of storage and data transfer, whereas our CPU-based implementation uses efficient sparse matrix computations and is suitable for large sparse datasets. For the community detection problem, we demonstrate accuracy and computational efficiency on Facebook, Yelp and DBLP datasets, and for the topic modeling problem, we also demonstrate good performance on the New York Times dataset. We compare our results to the state-of-the-art algorithms such as the variational method, and report a gain of accuracy and a gain of several orders of magnitude in the execution time.

Convolutional Dictionary Learning through Tensor Factorization

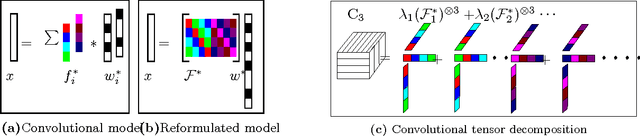
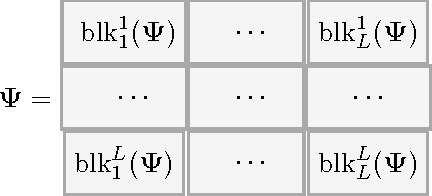
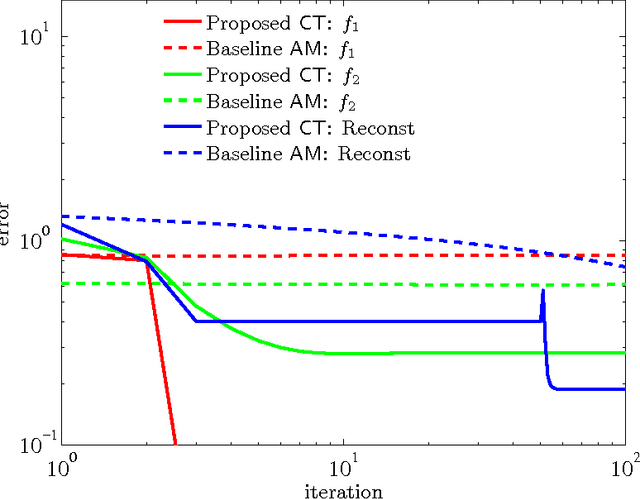
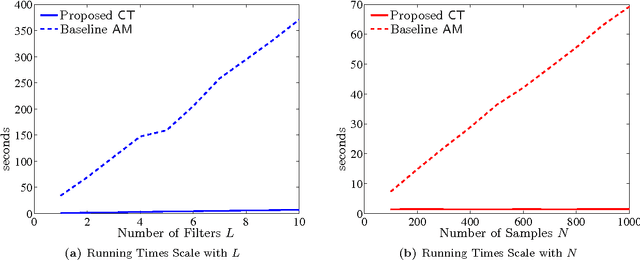
Tensor methods have emerged as a powerful paradigm for consistent learning of many latent variable models such as topic models, independent component analysis and dictionary learning. Model parameters are estimated via CP decomposition of the observed higher order input moments. However, in many domains, additional invariances such as shift invariances exist, enforced via models such as convolutional dictionary learning. In this paper, we develop novel tensor decomposition algorithms for parameter estimation of convolutional models. Our algorithm is based on the popular alternating least squares method, but with efficient projections onto the space of stacked circulant matrices. Our method is embarrassingly parallel and consists of simple operations such as fast Fourier transforms and matrix multiplications. Our algorithm converges to the dictionary much faster and more accurately compared to the alternating minimization over filters and activation maps.

Guaranteed Non-Orthogonal Tensor Decomposition via Alternating Rank-$1$ Updates

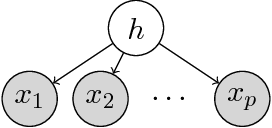
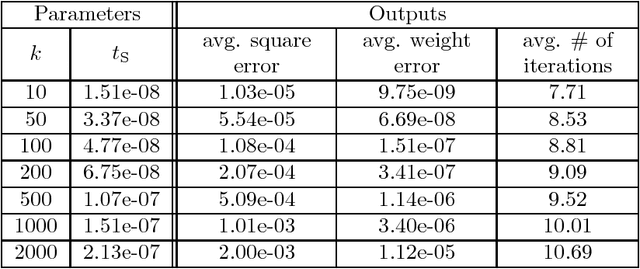
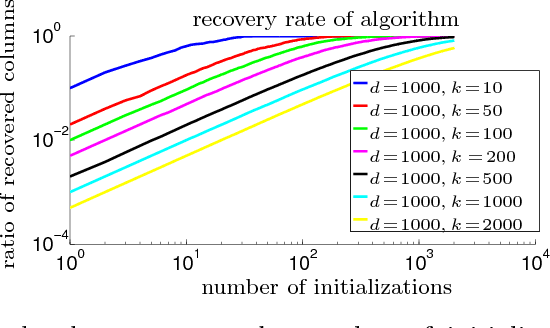
In this paper, we provide local and global convergence guarantees for recovering CP (Candecomp/Parafac) tensor decomposition. The main step of the proposed algorithm is a simple alternating rank-$1$ update which is the alternating version of the tensor power iteration adapted for asymmetric tensors. Local convergence guarantees are established for third order tensors of rank $k$ in $d$ dimensions, when $k=o \bigl( d^{1.5} \bigr)$ and the tensor components are incoherent. Thus, we can recover overcomplete tensor decomposition. We also strengthen the results to global convergence guarantees under stricter rank condition $k \le \beta d$ (for arbitrary constant $\beta > 1$) through a simple initialization procedure where the algorithm is initialized by top singular vectors of random tensor slices. Furthermore, the approximate local convergence guarantees for $p$-th order tensors are also provided under rank condition $k=o \bigl( d^{p/2} \bigr)$. The guarantees also include tight perturbation analysis given noisy tensor.

Sample Complexity Analysis for Learning Overcomplete Latent Variable Models through Tensor Methods

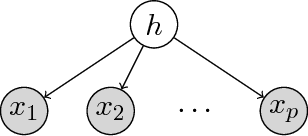
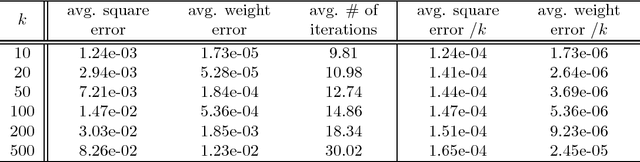
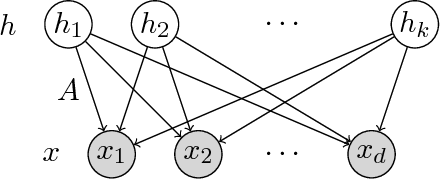
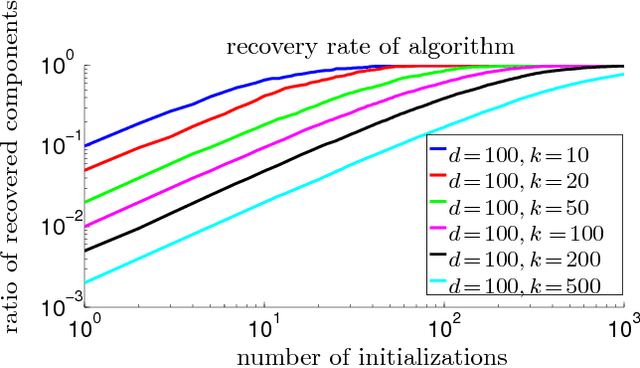
We provide guarantees for learning latent variable models emphasizing on the overcomplete regime, where the dimensionality of the latent space can exceed the observed dimensionality. In particular, we consider multiview mixtures, spherical Gaussian mixtures, ICA, and sparse coding models. We provide tight concentration bounds for empirical moments through novel covering arguments. We analyze parameter recovery through a simple tensor power update algorithm. In the semi-supervised setting, we exploit the label or prior information to get a rough estimate of the model parameters, and then refine it using the tensor method on unlabeled samples. We establish that learning is possible when the number of components scales as $k=o(d^{p/2})$, where $d$ is the observed dimension, and $p$ is the order of the observed moment employed in the tensor method. Our concentration bound analysis also leads to minimax sample complexity for semi-supervised learning of spherical Gaussian mixtures. In the unsupervised setting, we use a simple initialization algorithm based on SVD of the tensor slices, and provide guarantees under the stricter condition that $k\le \beta d$ (where constant $\beta$ can be larger than $1$), where the tensor method recovers the components under a polynomial running time (and exponential in $\beta$). Our analysis establishes that a wide range of overcomplete latent variable models can be learned efficiently with low computational and sample complexity through tensor decomposition methods.

Non-convex Robust PCA

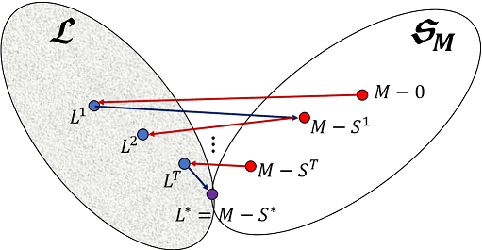
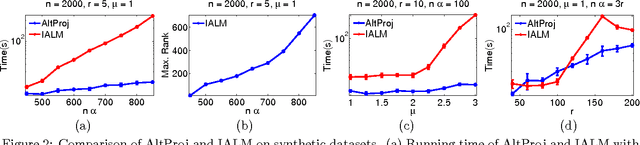
We propose a new method for robust PCA -- the task of recovering a low-rank matrix from sparse corruptions that are of unknown value and support. Our method involves alternating between projecting appropriate residuals onto the set of low-rank matrices, and the set of sparse matrices; each projection is {\em non-convex} but easy to compute. In spite of this non-convexity, we establish exact recovery of the low-rank matrix, under the same conditions that are required by existing methods (which are based on convex optimization). For an $m \times n$ input matrix ($m \leq n)$, our method has a running time of $O(r^2mn)$ per iteration, and needs $O(\log(1/\epsilon))$ iterations to reach an accuracy of $\epsilon$. This is close to the running time of simple PCA via the power method, which requires $O(rmn)$ per iteration, and $O(\log(1/\epsilon))$ iterations. In contrast, existing methods for robust PCA, which are based on convex optimization, have $O(m^2n)$ complexity per iteration, and take $O(1/\epsilon)$ iterations, i.e., exponentially more iterations for the same accuracy. Experiments on both synthetic and real data establishes the improved speed and accuracy of our method over existing convex implementations.