AAD-LLM: Adaptive Anomaly Detection Using Large Language Models

For data-constrained, complex and dynamic industrial environments, there is a critical need for transferable and multimodal methodologies to enhance anomaly detection and therefore, prevent costs associated with system failures. Typically, traditional PdM approaches are not transferable or multimodal. This work examines the use of Large Language Models (LLMs) for anomaly detection in complex and dynamic manufacturing systems. The research aims to improve the transferability of anomaly detection models by leveraging Large Language Models (LLMs) and seeks to validate the enhanced effectiveness of the proposed approach in data-sparse industrial applications. The research also seeks to enable more collaborative decision-making between the model and plant operators by allowing for the enriching of input series data with semantics. Additionally, the research aims to address the issue of concept drift in dynamic industrial settings by integrating an adaptability mechanism. The literature review examines the latest developments in LLM time series tasks alongside associated adaptive anomaly detection methods to establish a robust theoretical framework for the proposed architecture. This paper presents a novel model framework (AAD-LLM) that doesn't require any training or finetuning on the dataset it is applied to and is multimodal. Results suggest that anomaly detection can be converted into a "language" task to deliver effective, context-aware detection in data-constrained industrial applications. This work, therefore, contributes significantly to advancements in anomaly detection methodologies.

Trustworthy Artificial Intelligence in the Context of Metrology

We review research at the National Physical Laboratory (NPL) in the area of trustworthy artificial intelligence (TAI), and more specifically trustworthy machine learning (TML), in the context of metrology, the science of measurement. We describe three broad themes of TAI: technical, socio-technical and social, which play key roles in ensuring that the developed models are trustworthy and can be relied upon to make responsible decisions. From a metrology perspective we emphasise uncertainty quantification (UQ), and its importance within the framework of TAI to enhance transparency and trust in the outputs of AI systems. We then discuss three research areas within TAI that we are working on at NPL, and examine the certification of AI systems in terms of adherence to the characteristics of TAI.

Analytical results for uncertainty propagation through trained machine learning regression models

Machine learning (ML) models are increasingly being used in metrology applications. However, for ML models to be credible in a metrology context they should be accompanied by principled uncertainty quantification. This paper addresses the challenge of uncertainty propagation through trained/fixed machine learning (ML) regression models. Analytical expressions for the mean and variance of the model output are obtained/presented for certain input data distributions and for a variety of ML models. Our results cover several popular ML models including linear regression, penalised linear regression, kernel ridge regression, Gaussian Processes (GPs), support vector machines (SVMs) and relevance vector machines (RVMs). We present numerical experiments in which we validate our methods and compare them with a Monte Carlo approach from a computational efficiency point of view. We also illustrate our methods in the context of a metrology application, namely modelling the state-of-health of lithium-ion cells based upon Electrical Impedance Spectroscopy (EIS) data

A divide-and-conquer algorithm for binary matrix completion

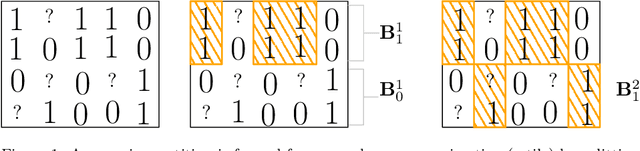
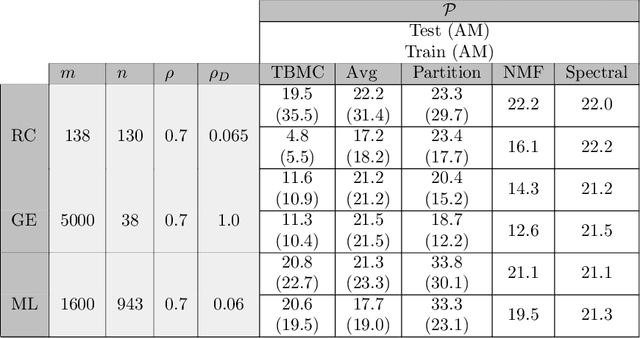
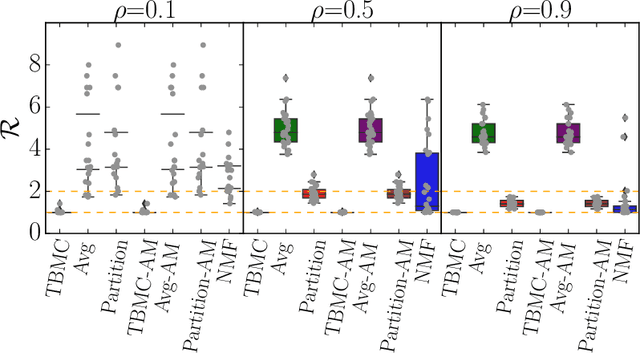
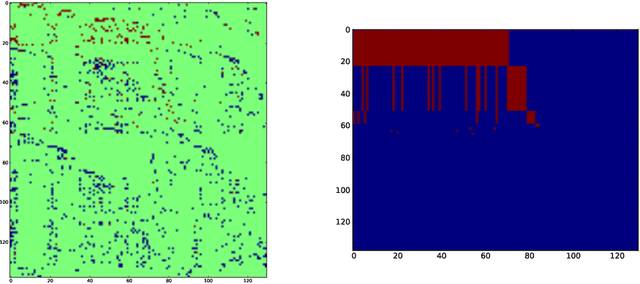
We propose an algorithm for low rank matrix completion for matrices with binary entries which obtains explicit binary factors. Our algorithm, which we call TBMC (\emph{Tiling for Binary Matrix Completion}), gives interpretable output in the form of binary factors which represent a decomposition of the matrix into tiles. Our approach is inspired by a popular algorithm from the data mining community called PROXIMUS: it adopts the same recursive partitioning approach while extending to missing data. The algorithm relies upon rank-one approximations of incomplete binary matrices, and we propose a linear programming (LP) approach for solving this subproblem. We also prove a $2$-approximation result for the LP approach which holds for any level of subsampling and for any subsampling pattern. Our numerical experiments show that TBMC outperforms existing methods on recommender systems arising in the context of real datasets.

Sketching for Sequential Change-Point Detection

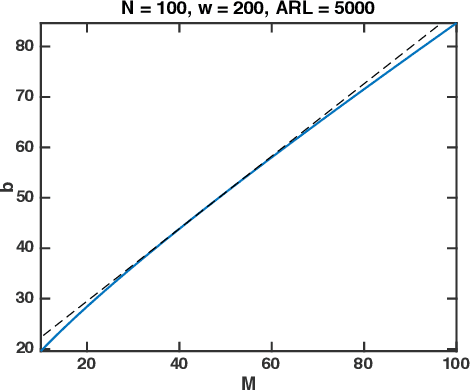
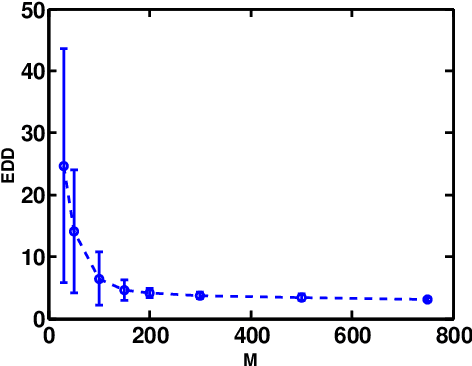
We study sequential change-point detection procedures based on linear sketches of high-dimensional signal vectors using generalized likelihood ratio (GLR) statistics. The GLR statistics allow for an unknown post-change mean that represents an anomaly or novelty. We consider both fixed and time-varying projections, derive theoretical approximations to two fundamental performance metrics: the average run length (ARL) and the expected detection delay (EDD); these approximations are shown to be highly accurate by numerical simulations. We further characterize the relative performance measure of the sketching procedure compared to that without sketching and show that there can be little performance loss when the signal strength is sufficiently large, and enough number of sketches are used. Finally, we demonstrate the good performance of sketching procedures using simulation and real-data examples on solar flare detection and failure detection in power networks.

DCTNet and PCANet for acoustic signal feature extraction

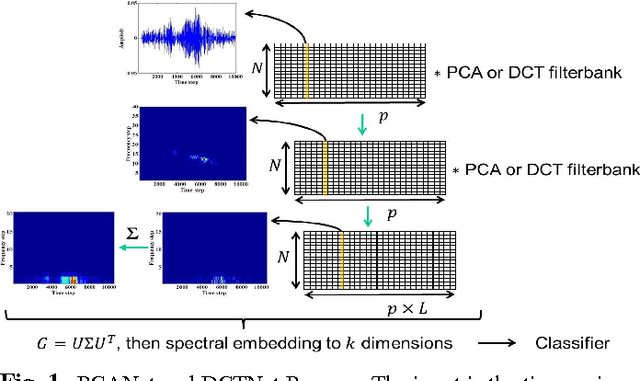
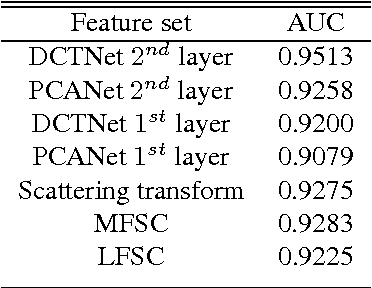
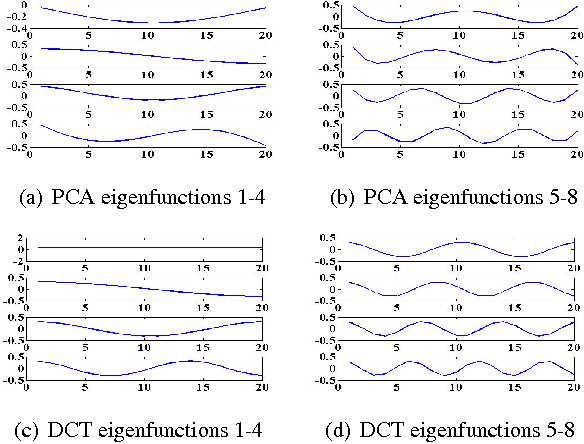
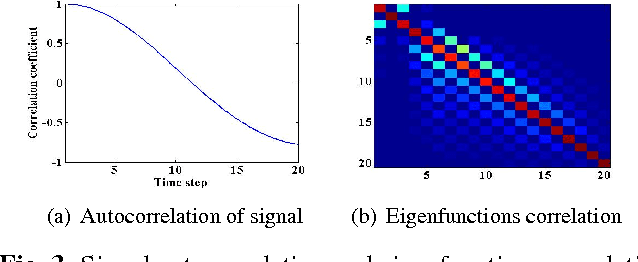
We introduce the use of DCTNet, an efficient approximation and alternative to PCANet, for acoustic signal classification. In PCANet, the eigenfunctions of the local sample covariance matrix (PCA) are used as filterbanks for convolution and feature extraction. When the eigenfunctions are well approximated by the Discrete Cosine Transform (DCT) functions, each layer of of PCANet and DCTNet is essentially a time-frequency representation. We relate DCTNet to spectral feature representation methods, such as the the short time Fourier transform (STFT), spectrogram and linear frequency spectral coefficients (LFSC). Experimental results on whale vocalization data show that DCTNet improves classification rate, demonstrating DCTNet's applicability to signal processing problems such as underwater acoustics.

Data Representation using the Weyl Transform

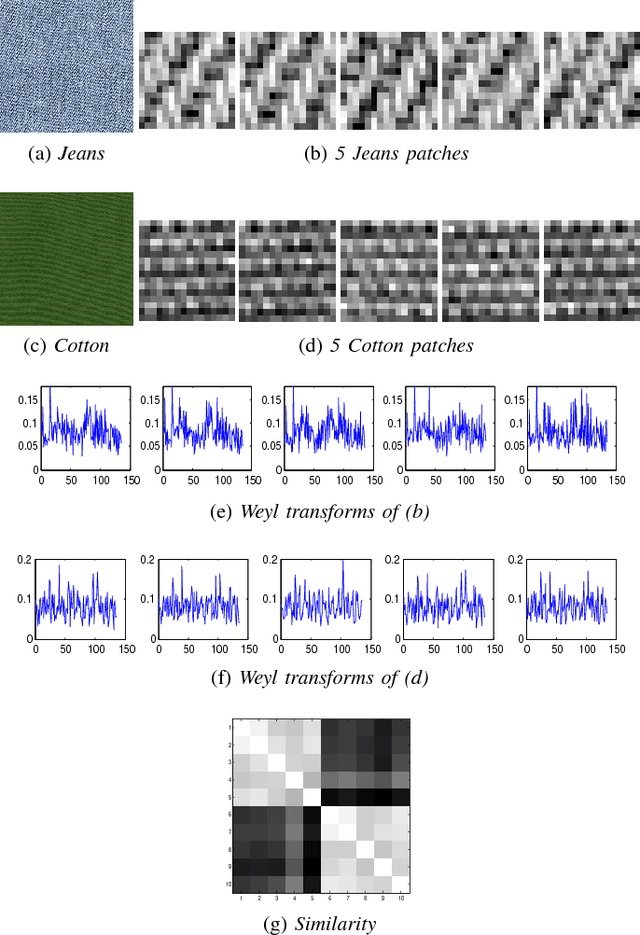
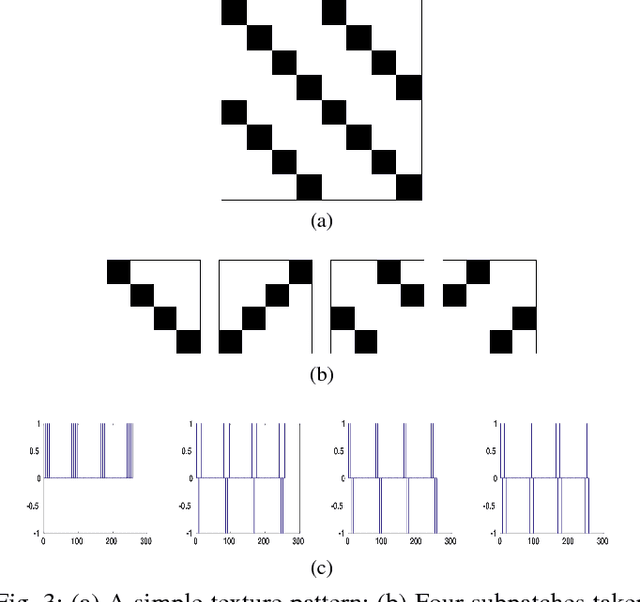
The Weyl transform is introduced as a rich framework for data representation. Transform coefficients are connected to the Walsh-Hadamard transform of multiscale autocorrelations, and different forms of dyadic periodicity in a signal are shown to appear as different features in its Weyl coefficients. The Weyl transform has a high degree of symmetry with respect to a large group of multiscale transformations, which allows compact yet discriminative representations to be obtained by pooling coefficients. The effectiveness of the Weyl transform is demonstrated through the example of textured image classification.