The Tractability Landscape of Sampling with Inexact Scores

We provide a simple and tight characterization of the types of inexact score oracle access that permit sampling with vanishing total variation bias, for a standard, well-behaved target family. Our main result shows that any weaker error than the sub-Gaussian assumption used by [YW26] rules out the tractability of unbiased sampling. This strengthens the conclusion of [CCSW26] to be algorithm-agnostic, and to hold for a wider range of error assumptions.

Functional Stochastic Localization

Eldan's stochastic localization is a probabilistic construction that has proved instrumental to modern breakthroughs in high-dimensional geometry and the design of sampling algorithms. Motivated by sampling under non-Euclidean geometries and the mirror descent algorithm in optimization, we develop a functional generalization of Eldan's process that replaces Gaussian regularization with regularization by any positive integer multiple of a log-Laplace transform. We further give a mixing time bound on the Markov chain induced by our localization process, which holds if our target distribution satisfies a functional Poincaré inequality. Finally, we apply our framework to differentially private convex optimization in $\ell_p$ norms for $p \in [1, 2)$, where we improve state-of-the-art query complexities in a zeroth-order model.

Private Continuous-Time Synthetic Trajectory Generation via Mean-Field Langevin Dynamics

We provide an algorithm to privately generate continuous-time data (e.g. marginals from stochastic differential equations), which has applications in highly sensitive domains involving time-series data such as healthcare. We leverage the connections between trajectory inference and continuous-time synthetic data generation, along with a computational method based on mean-field Langevin dynamics. As discretized mean-field Langevin dynamics and noisy particle gradient descent are equivalent, DP results for noisy SGD can be applied to our setting. We provide experiments that generate realistic trajectories on a synthesized variation of hand-drawn MNIST data while maintaining meaningful privacy guarantees. Crucially, our method has strong utility guarantees under the setting where each person contributes data for \emph{only one time point}, while prior methods require each person to contribute their \emph{entire temporal trajectory}--directly improving the privacy characteristics by construction.

Mirror Mean-Field Langevin Dynamics

The mean-field Langevin dynamics (MFLD) minimizes an entropy-regularized nonlinear convex functional on the Wasserstein space over $\mathbb{R}^d$, and has gained attention recently as a model for the gradient descent dynamics of interacting particle systems such as infinite-width two-layer neural networks. However, many problems of interest have constrained domains, which are not solved by existing mean-field algorithms due to the global diffusion term. We study the optimization of probability measures constrained to a convex subset of $\mathbb{R}^d$ by proposing the \emph{mirror mean-field Langevin dynamics} (MMFLD), an extension of MFLD to the mirror Langevin framework. We obtain linear convergence guarantees for the continuous MMFLD via a uniform log-Sobolev inequality, and uniform-in-time propagation of chaos results for its time- and particle-discretized counterpart.

Compute-Optimal LLMs Provably Generalize Better With Scale

Why do larger language models generalize better? To investigate this question, we develop generalization bounds on the pretraining objective of large language models (LLMs) in the compute-optimal regime, as described by the Chinchilla scaling laws. We introduce a novel, fully empirical Freedman-type martingale concentration inequality that tightens existing bounds by accounting for the variance of the loss function. This generalization bound can be decomposed into three interpretable components: the number of parameters per token, the loss variance, and the quantization error at a fixed bitrate. As compute-optimal language models are scaled up, the number of parameters per data point remains constant; however, both the loss variance and the quantization error decrease, implying that larger models should have smaller generalization gaps. We examine why larger models tend to be more quantizable from an information theoretic perspective, showing that the rate at which they can integrate new information grows more slowly than their capacity on the compute-optimal frontier. From these findings we produce a scaling law for the generalization gap, with bounds that become predictably stronger with scale.

Partially Observed Trajectory Inference using Optimal Transport and a Dynamics Prior

Trajectory inference seeks to recover the temporal dynamics of a population from snapshots of its (uncoupled) temporal marginals, i.e. where observed particles are not tracked over time. Lavenant et al. arXiv:2102.09204 addressed this challenging problem under a stochastic differential equation (SDE) model with a gradient-driven drift in the observed space, introducing a minimum entropy estimator relative to the Wiener measure. Chizat et al. arXiv:2205.07146 then provided a practical grid-free mean-field Langevin (MFL) algorithm using Schr\"odinger bridges. Motivated by the overwhelming success of observable state space models in the traditional paired trajectory inference problem (e.g. target tracking), we extend the above framework to a class of latent SDEs in the form of observable state space models. In this setting, we use partial observations to infer trajectories in the latent space under a specified dynamics model (e.g. the constant velocity/acceleration models from target tracking). We introduce PO-MFL to solve this latent trajectory inference problem and provide theoretical guarantees by extending the results of arXiv:2102.09204 to the partially observed setting. We leverage the MFL framework of arXiv:2205.07146, yielding an algorithm based on entropic OT between dynamics-adjusted adjacent time marginals. Experiments validate the robustness of our method and the exponential convergence of the MFL dynamics, and demonstrate significant outperformance over the latent-free method of arXiv:2205.07146 in key scenarios.

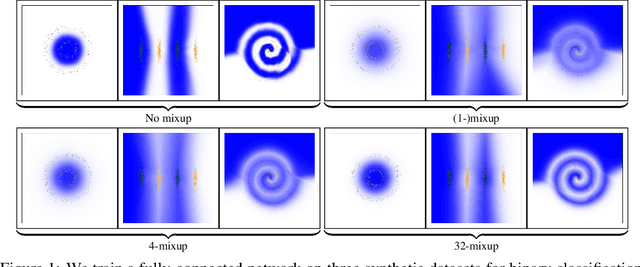
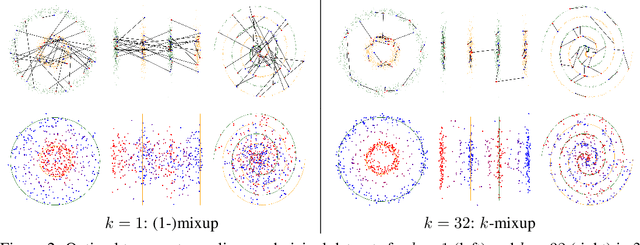
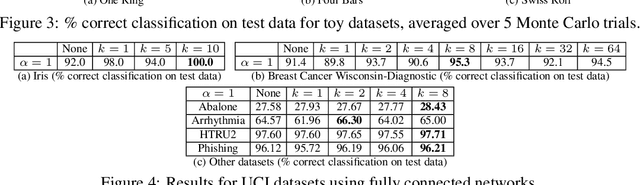
k-Mixup Regularization for Deep Learning via Optimal Transport

Mixup is a popular regularization technique for training deep neural networks that can improve generalization and increase adversarial robustness. It perturbs input training data in the direction of other randomly-chosen instances in the training set. To better leverage the structure of the data, we extend mixup to \emph{$k$-mixup} by perturbing $k$-batches of training points in the direction of other $k$-batches using displacement interpolation, interpolation under the Wasserstein metric. We demonstrate theoretically and in simulations that $k$-mixup preserves cluster and manifold structures, and we extend theory studying efficacy of standard mixup. Our empirical results show that training with $k$-mixup further improves generalization and robustness on benchmark datasets.