Top Two Algorithms Revisited

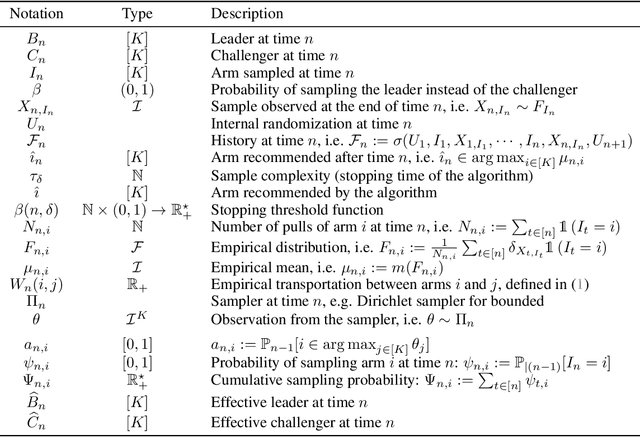
Top Two algorithms arose as an adaptation of Thompson sampling to best arm identification in multi-armed bandit models (Russo, 2016), for parametric families of arms. They select the next arm to sample from by randomizing among two candidate arms, a leader and a challenger. Despite their good empirical performance, theoretical guarantees for fixed-confidence best arm identification have only been obtained when the arms are Gaussian with known variances. In this paper, we provide a general analysis of Top Two methods, which identifies desirable properties of the leader, the challenger, and the (possibly non-parametric) distributions of the arms. As a result, we obtain theoretically supported Top Two algorithms for best arm identification with bounded distributions. Our proof method demonstrates in particular that the sampling step used to select the leader inherited from Thompson sampling can be replaced by other choices, like selecting the empirical best arm.

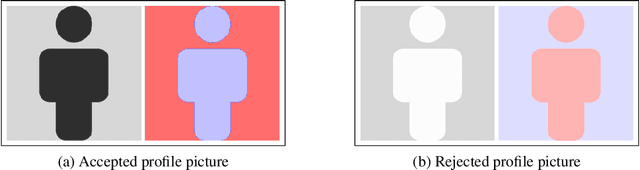
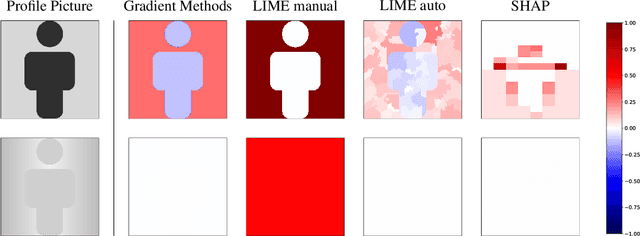
Attribution-based Explanations that Provide Recourse Cannot be Robust

Different users of machine learning methods require different explanations, depending on their goals. To make machine learning accountable to society, one important goal is to get actionable options for recourse, which allow an affected user to change the decision $f(x)$ of a machine learning system by making limited changes to its input $x$. We formalize this by providing a general definition of recourse sensitivity, which needs to be instantiated with a utility function that describes which changes to the decisions are relevant to the user. This definition applies to local attribution methods, which attribute an importance weight to each input feature. It is often argued that such local attributions should be robust, in the sense that a small change in the input $x$ that is being explained, should not cause a large change in the feature weights. However, we prove formally that it is in general impossible for any single attribution method to be both recourse sensitive and robust at the same time. It follows that there must always exist counterexamples to at least one of these properties. We provide such counterexamples for several popular attribution methods, including LIME, SHAP, Integrated Gradients and SmoothGrad. Our results also cover counterfactual explanations, which may be viewed as attributions that describe a perturbation of $x$. We further discuss possible ways to work around our impossibility result, for instance by allowing the output to consist of sets with multiple attributions. Finally, we strengthen our impossibility result for the restricted case where users are only able to change a single attribute of x, by providing an exact characterization of the functions $f$ to which impossibility applies.

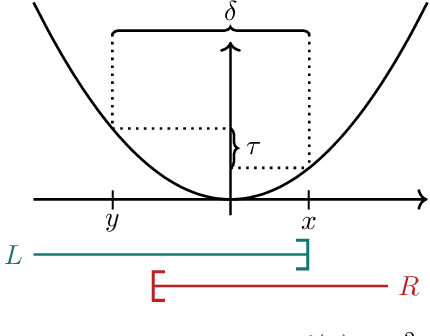
Bandits with many optimal arms

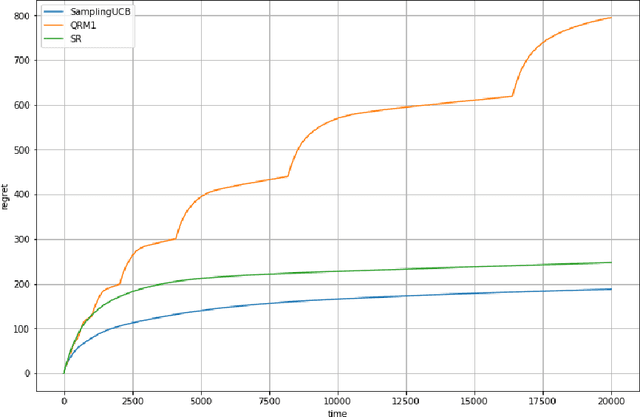
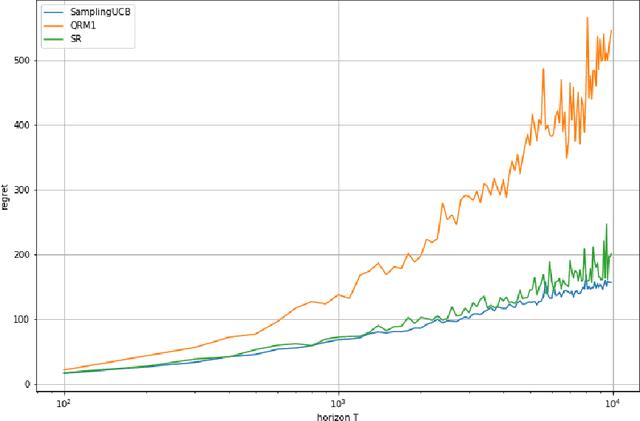
We consider a stochastic bandit problem with a possibly infinite number of arms. We write $p^*$ for the proportion of optimal arms and $\Delta$ for the minimal mean-gap between optimal and sub-optimal arms. We characterize the optimal learning rates both in the cumulative regret setting, and in the best-arm identification setting in terms of the problem parameters $T$ (the budget), $p^*$ and $\Delta$. For the objective of minimizing the cumulative regret, we provide a lower bound of order $\Omega(\log(T)/(p^*\Delta))$ and a UCB-style algorithm with matching upper bound up to a factor of $\log(1/\Delta)$. Our algorithm needs $p^*$ to calibrate its parameters, and we prove that this knowledge is necessary, since adapting to $p^*$ in this setting is impossible. For best-arm identification we also provide a lower bound of order $\Omega(\exp(-cT\Delta^2p^*))$ on the probability of outputting a sub-optimal arm where $c>0$ is an absolute constant. We also provide an elimination algorithm with an upper bound matching the lower bound up to a factor of order $\log(1/\Delta)$ in the exponential, and that does not need $p^*$ or $\Delta$ as parameter.

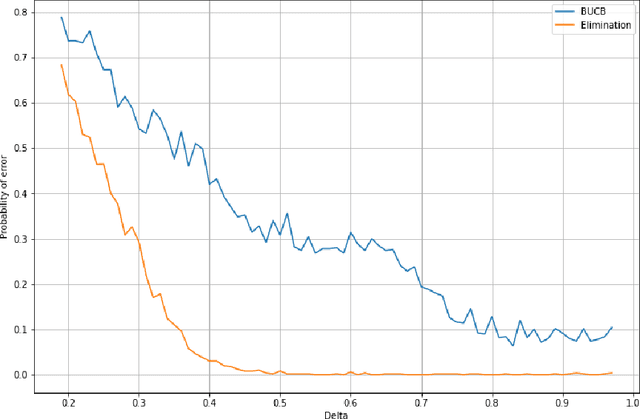
Fixed-Confidence Guarantees for Bayesian Best-Arm Identification

We investigate and provide new insights on the sampling rule called Top-Two Thompson Sampling (TTTS). In particular, we justify its use for fixed-confidence best-arm identification. We further propose a variant of TTTS called Top-Two Transportation Cost (T3C), which disposes of the computational burden of TTTS. As our main contribution, we provide the first sample complexity analysis of TTTS and T3C when coupled with a very natural Bayesian stopping rule, for bandits with Gaussian rewards, solving one of the open questions raised by Russo (2016). We also provide new posterior convergence results for TTTS under two models that are commonly used in practice: bandits with Gaussian and Bernoulli rewards and conjugate priors.

Safe-Bayesian Generalized Linear Regression

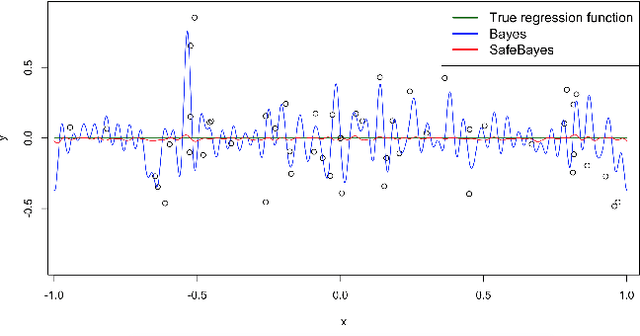
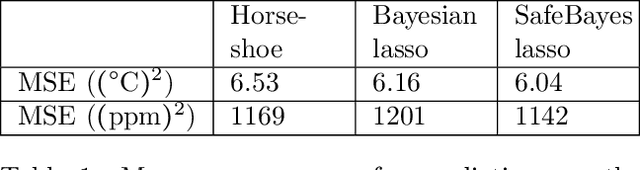
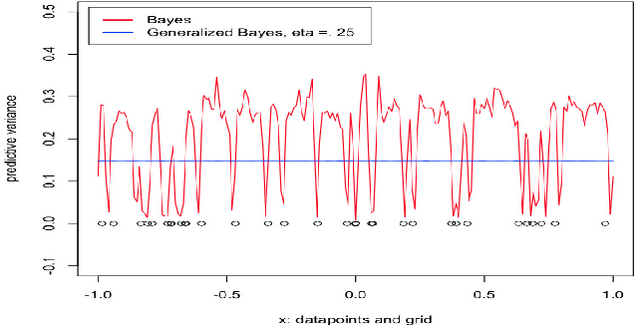
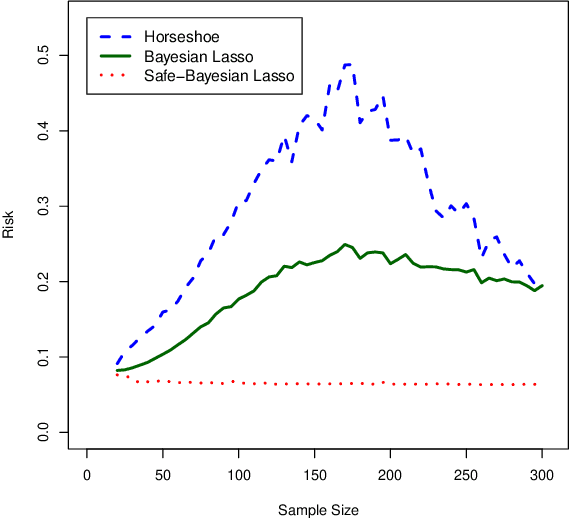
We study generalized Bayesian inference under misspecification, i.e. when the model is `wrong but useful'. Generalized Bayes equips the likelihood with a learning rate $\eta$. We show that for generalized linear models (GLMs), $\eta$-generalized Bayes concentrates around the best approximation of the truth within the model for specific $\eta \neq 1$, even under severely misspecified noise, as long as the tails of the true distribution are exponential. We then derive MCMC samplers for generalized Bayesian lasso and logistic regression, and give examples of both simulated and real-world data in which generalized Bayes outperforms standard Bayes by a vast margin.

Safe Testing

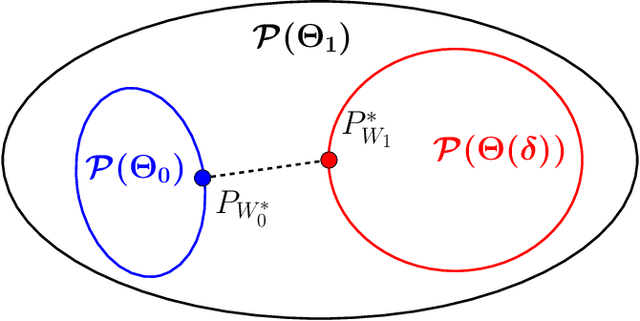
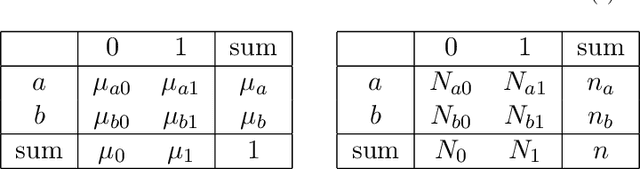
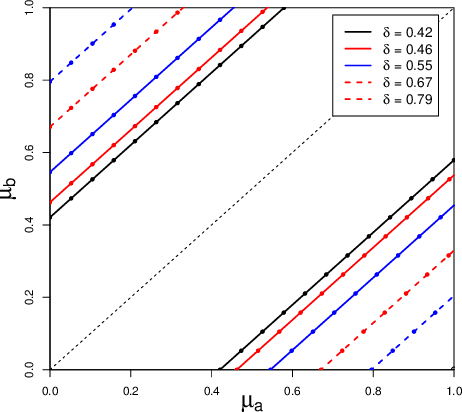
We present a new theory of hypothesis testing. The main concept is the S-value, a notion of evidence which, unlike p-values, allows for effortlessly combining evidence from several tests, even in the common scenario where the decision to perform a new test depends on the previous test outcome: safe tests based on S-values generally preserve Type-I error guarantees under such "optional continuation". S-values exist for completely general testing problems with composite null and alternatives. Their prime interpretation is in terms of gambling or investing, each S-value corresponding to a particular investment. Surprisingly, optimal "GROW" S-values, which lead to fastest capital growth, are fully characterized by the joint information projection (JIPr) between the set of all Bayes marginal distributions on H0 and H1. Thus, optimal S-values also have an interpretation as Bayes factors, with priors given by the JIPr. We illustrate the theory using two classical testing scenarios: the one-sample t-test and the 2x2 contingency table. In the t-test setting, GROW s-values correspond to adopting the right Haar prior on the variance, like in Jeffreys' Bayesian t-test. However, unlike Jeffreys', the "default" safe t-test puts a discrete 2-point prior on the effect size, leading to better behavior in terms of statistical power. Sharing Fisherian, Neymanian and Jeffreys-Bayesian interpretations, S-values and safe tests may provide a methodology acceptable to adherents of all three schools.

Optional Stopping with Bayes Factors: a categorization and extension of folklore results, with an application to invariant situations

It is often claimed that Bayesian methods, in particular Bayes factor methods for hypothesis testing, can deal with optional stopping. We first give an overview, using only most elementary probability theory, of three different mathematical meanings that various authors give to this claim: stopping rule independence, posterior calibration and (semi-) frequentist robustness to optional stopping. We then prove theorems to the effect that - while their practical implications are sometimes debatable - these claims do indeed hold in a general measure-theoretic setting. The novelty here is that we allow for nonintegrable measures based on improper priors, which leads to particularly strong results for the practically important case of models satisfying a group invariance (such as location or scale). When equipped with the right Haar prior, calibration and semi-frequentist robustness to optional stopping hold uniformly irrespective of the value of the underlying nuisance parameter, as long as the stopping rule satisfies a certain intuitive property.