Active Ranking of Experts Based on their Performances in Many Tasks

We consider the problem of ranking n experts based on their performances on d tasks. We make a monotonicity assumption stating that for each pair of experts, one outperforms the other on all tasks. We consider the sequential setting where in each round, the learner has access to noisy evaluations of actively chosen pair of expert-task, given the information available up to the actual round. Given a confidence parameter $\delta$ $\in$ (0, 1), we provide strategies allowing to recover the correct ranking of experts and develop a bound on the total number of queries made by our algorithm that hold with probability at least 1 -- $\delta$. We show that our strategy is adaptive to the complexity of the problem (our bounds are instance dependent), and develop matching lower bounds up to a poly-logarithmic factor. Finally, we adapt our strategy to the relaxed problem of best expert identification and provide numerical simulation consistent with our theoretical results.

Covariance Adaptive Best Arm Identification

We consider the problem of best arm identification in the multi-armed bandit model, under fixed confidence. Given a confidence input $\delta$, the goal is to identify the arm with the highest mean reward with a probability of at least 1 -- $\delta$, while minimizing the number of arm pulls. While the literature provides solutions to this problem under the assumption of independent arms distributions, we propose a more flexible scenario where arms can be dependent and rewards can be sampled simultaneously. This framework allows the learner to estimate the covariance among the arms distributions, enabling a more efficient identification of the best arm. The relaxed setting we propose is relevant in various applications, such as clinical trials, where similarities between patients or drugs suggest underlying correlations in the outcomes. We introduce new algorithms that adapt to the unknown covariance of the arms and demonstrate through theoretical guarantees that substantial improvement can be achieved over the standard setting. Additionally, we provide new lower bounds for the relaxed setting and present numerical simulations that support their theoretical findings.

Constant regret for sequence prediction with limited advice

We investigate the problem of cumulative regret minimization for individual sequence prediction with respect to the best expert in a finite family of size K under limited access to information. We assume that in each round, the learner can predict using a convex combination of at most p experts for prediction, then they can observe a posteriori the losses of at most m experts. We assume that the loss function is range-bounded and exp-concave. In the standard multi-armed bandits setting, when the learner is allowed to play only one expert per round and observe only its feedback, known optimal regret bounds are of the order O($\sqrt$ KT). We show that allowing the learner to play one additional expert per round and observe one additional feedback improves substantially the guarantees on regret. We provide a strategy combining only p = 2 experts per round for prediction and observing m $\ge$ 2 experts' losses. Its randomized regret (wrt. internal randomization of the learners' strategy) is of order O (K/m) log(K$\delta$ --1) with probability 1 -- $\delta$, i.e., is independent of the horizon T ("constant" or "fast rate" regret) if (p $\ge$ 2 and m $\ge$ 3). We prove that this rate is optimal up to a logarithmic factor in K. In the case p = m = 2, we provide an upper bound of order O(K 2 log(K$\delta$ --1)), with probability 1 -- $\delta$. Our strategies do not require any prior knowledge of the horizon T nor of the confidence parameter $\delta$. Finally, we show that if the learner is constrained to observe only one expert feedback per round, the worst-case regret is the "slow rate" $\Omega$($\sqrt$ KT), suggesting that synchronous observation of at least two experts per round is necessary to have a constant regret.

Fast rates for prediction with limited expert advice

We investigate the problem of minimizing the excess generalization error with respect to the best expert prediction in a finite family in the stochastic setting, under limited access to information. We assume that the learner only has access to a limited number of expert advices per training round, as well as for prediction. Assuming that the loss function is Lipschitz and strongly convex, we show that if we are allowed to see the advice of only one expert per round for T rounds in the training phase, or to use the advice of only one expert for prediction in the test phase, the worst-case excess risk is $\Omega$(1/ $\sqrt$ T) with probability lower bounded by a constant. However, if we are allowed to see at least two actively chosen expert advices per training round and use at least two experts for prediction, the fast rate O(1/T) can be achieved. We design novel algorithms achieving this rate in this setting, and in the setting where the learner has a budget constraint on the total number of observed expert advices, and give precise instance-dependent bounds on the number of training rounds and queries needed to achieve a given generalization error precision.

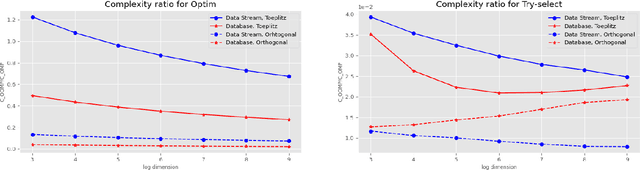
Online Orthogonal Matching Pursuit

Greedy algorithms for feature selection are widely used for recovering sparse high-dimensional vectors in linear models. In classical procedures, the main emphasis was put on the sample complexity, with little or no consideration of the computation resources required. We present a novel online algorithm: Online Orthogonal Matching Pursuit (OOMP) for online support recovery in the random design setting of sparse linear regression. Our procedure selects features sequentially, alternating between allocation of samples only as needed to candidate features, and optimization over the selected set of variables to estimate the regression coefficients. Theoretical guarantees about the output of this algorithm are proven and its computational complexity is analysed.