Demographic parity in regression and classification within the unawareness framework

This paper explores the theoretical foundations of fair regression under the constraint of demographic parity within the unawareness framework, where disparate treatment is prohibited, extending existing results where such treatment is permitted. Specifically, we aim to characterize the optimal fair regression function when minimizing the quadratic loss. Our results reveal that this function is given by the solution to a barycenter problem with optimal transport costs. Additionally, we study the connection between optimal fair cost-sensitive classification, and optimal fair regression. We demonstrate that nestedness of the decision sets of the classifiers is both necessary and sufficient to establish a form of equivalence between classification and regression. Under this nestedness assumption, the optimal classifiers can be derived by applying thresholds to the optimal fair regression function; conversely, the optimal fair regression function is characterized by the family of cost-sensitive classifiers.

Improved Algorithms for Contextual Dynamic Pricing

In contextual dynamic pricing, a seller sequentially prices goods based on contextual information. Buyers will purchase products only if the prices are below their valuations. The goal of the seller is to design a pricing strategy that collects as much revenue as possible. We focus on two different valuation models. The first assumes that valuations linearly depend on the context and are further distorted by noise. Under minor regularity assumptions, our algorithm achieves an optimal regret bound of $\tilde{\mathcal{O}}(T^{2/3})$, improving the existing results. The second model removes the linearity assumption, requiring only that the expected buyer valuation is $\beta$-H\"older in the context. For this model, our algorithm obtains a regret $\tilde{\mathcal{O}}(T^{d+2\beta/d+3\beta})$, where $d$ is the dimension of the context space.

The price of unfairness in linear bandits with biased feedback

Artificial intelligence is increasingly used in a wide range of decision making scenarios with higher and higher stakes. At the same time, recent work has highlighted that these algorithms can be dangerously biased, and that their results often need to be corrected to avoid leading to unfair decisions. In this paper, we study the problem of sequential decision making with biased linear bandit feedback. At each round, a player selects an action described by a covariate and by a sensitive attribute. She receives a reward corresponding to the covariates of the action that she has chosen, but only observe a biased evaluation of this reward, where the bias depends on the sensitive attribute. To tackle this problem, we design a Fair Phased Elimination algorithm. We establish an upper bound on its worst-case regret, showing that it is smaller than C$\kappa$ 1/3 * log(T) 1/3 T 2/3 , where C is a numerical constant and $\kappa$ * an explicit geometrical constant characterizing the difficulty of bias estimation. The worst case regret is higher than the dT 1/2 log(T) regret rate obtained under unbiased feedback. We show that this rate cannot be improved for all instances : we obtain lower bounds on the worst-case regret for some sets of actions showing that this rate is tight up to a sub-logarithmic factor. We also obtain gap-dependent upper bounds on the regret, and establish matching lower bounds for some problem instance. Interestingly, the gap-dependent rates reveal the existence of non-trivial instances where the problem is no more difficult than its unbiased counterpart.

Hierarchical transfer learning with applications for electricity load forecasting

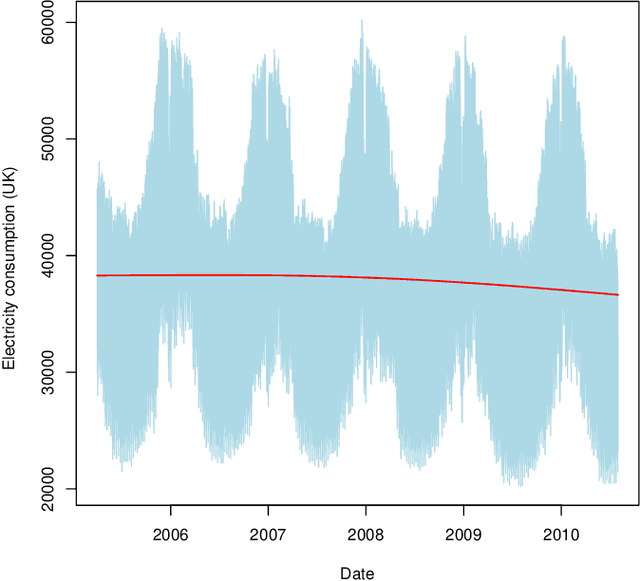
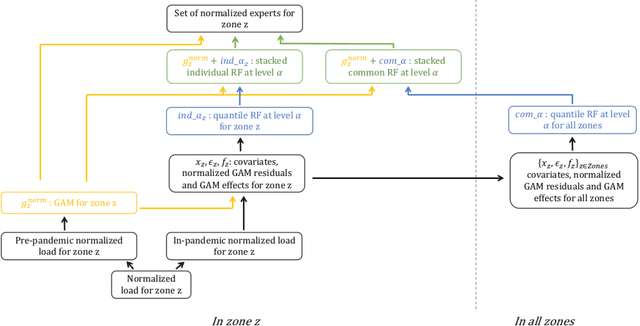
The recent abundance of data on electricity consumption at different scales opens new challenges and highlights the need for new techniques to leverage information present at finer scales in order to improve forecasts at wider scales. In this work, we take advantage of the similarity between this hierarchical prediction problem and multi-scale transfer learning. We develop two methods for hierarchical transfer learning, based respectively on the stacking of generalized additive models and random forests, and on the use of aggregation of experts. We apply these methods to two problems of electricity load forecasting at national scale, using smart meter data in the first case, and regional data in the second case. For these two usecases, we compare the performances of our methods to that of benchmark algorithms, and we investigate their behaviour using variable importance analysis. Our results demonstrate the interest of both methods, which lead to a significant improvement of the predictions.

Finite Continuum-Armed Bandits

We consider a situation where an agent has $T$ ressources to be allocated to a larger number $N$ of actions. Each action can be completed at most once and results in a stochastic reward with unknown mean. The goal of the agent is to maximize her cumulative reward. Non trivial strategies are possible when side information on the actions is available, for example in the form of covariates. Focusing on a nonparametric setting, where the mean reward is an unknown function of a one-dimensional covariate, we propose an optimal strategy for this problem. Under natural assumptions on the reward function, we prove that the optimal regret scales as $O(T^{1/3})$ up to poly-logarithmic factors when the budget $T$ is proportional to the number of actions $N$. When $T$ becomes small compared to $N$, a smooth transition occurs. When the ratio $T/N$ decreases from a constant to $N^{-1/3}$, the regret increases progressively up to the $O(T^{1/2})$ rate encountered in continuum-armed bandits.

Link Prediction in the Stochastic Block Model with Outliers

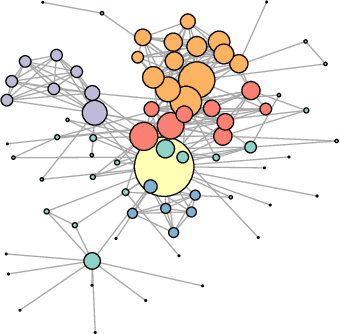
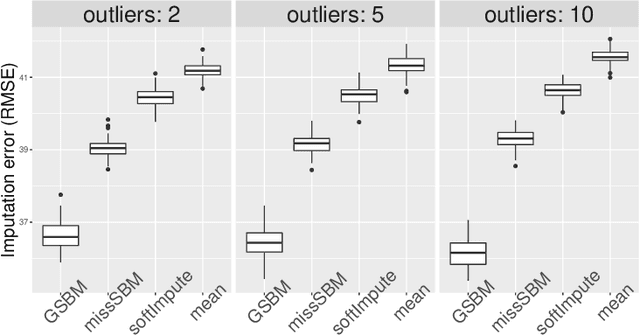
The Stochastic Block Model is a popular model for network analysis in the presence of community structure. However, in numerous examples, the assumptions underlying this classical model are put in default by the behaviour of a small number of outlier nodes such as hubs, nodes with mixed membership profiles, or corrupted nodes. In addition, real-life networks are likely to be incomplete, due to non-response or machine failures. We introduce a new algorithm to estimate the connection probabilities in a network, which is robust to both outlier nodes and missing observations. Under fairly general assumptions, this method detects the outliers, and achieves the best known error for the estimation of connection probabilities with polynomial computation cost. In addition, we prove sub-linear convergence of our algorithm. We provide a simulation study which demonstrates the good behaviour of the method in terms of outliers selection and prediction of the missing links.