Random projections and sampling algorithms for clustering of high-dimensional polygonal curves

We study the center and median clustering problems for high-dimensional polygonal curves with finite but unbounded complexity. We tackle the computational issue that arises from the high number of dimensions by defining a Johnson-Lindenstrauss projection for polygonal curves. We analyze the resulting error in terms of the Fr\'echet distance, which is a natural dissimilarity measure for curves. Our algorithms for the median clustering achieve sublinear dependency on the number of input curves via subsampling. For the center clustering we utilize Buchin et al. (2019a) algorithm that achieves linear running-time in the number of input curves. We evaluate our results empirically utilizing a fast, CUDA-parallelized variant of the Alt and Godau algorithm for the Fr\'echet distance. Our experiments show that our clustering algorithms have fast and accurate practical implementations that yield meaningful results on real world data from various physical domains.

A Theory-Based Evaluation of Nearest Neighbor Models Put Into Practice

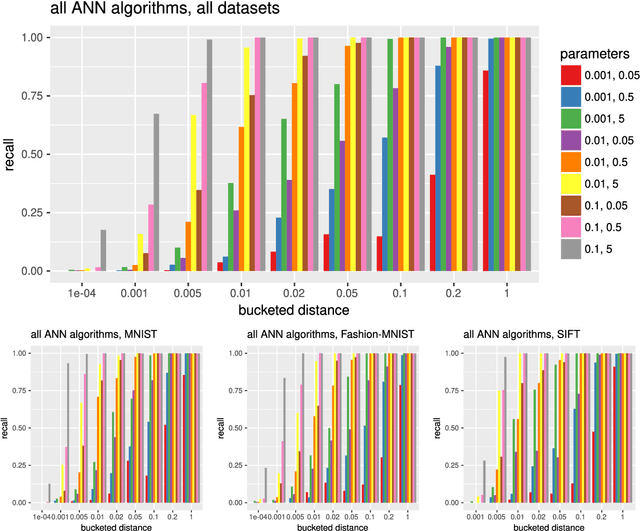
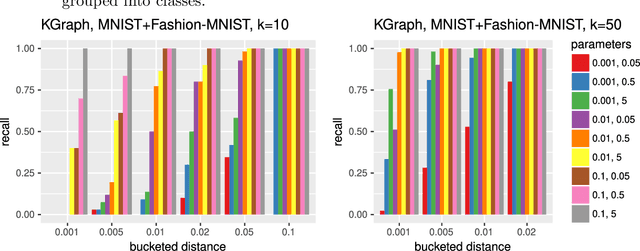
In the $k$-nearest neighborhood model ($k$-NN), we are given a set of points $P$, and we shall answer queries $q$ by returning the $k$ nearest neighbors of $q$ in $P$ according to some metric. This concept is crucial in many areas of data analysis and data processing, e.g., computer vision, document retrieval and machine learning. Many $k$-NN algorithms have been published and implemented, but often the relation between parameters and accuracy of the computed $k$-NN is not explicit. We study property testing of $k$-NN graphs in theory and evaluate it empirically: given a point set $P \subset \mathbb{R}^\delta$ and a directed graph $G=(P,E)$, is $G$ a $k$-NN graph, i.e., every point $p \in P$ has outgoing edges to its $k$ nearest neighbors, or is it $\epsilon$-far from being a $k$-NN graph? Here, $\epsilon$-far means that one has to change more than an $\epsilon$-fraction of the edges in order to make $G$ a $k$-NN graph. We develop a randomized algorithm with one-sided error that decides this question, i.e., a property tester for the $k$-NN property, with complexity $O(\sqrt{n} k^2 / \epsilon^2)$ measured in terms of the number of vertices and edges it inspects, and we prove a lower bound of $\Omega(\sqrt{n / \epsilon k})$. We evaluate our tester empirically on the $k$-NN models computed by various algorithms and show that it can be used to detect $k$-NN models with bad accuracy in significantly less time than the building time of the $k$-NN model.