$p$-Generalized Probit Regression and Scalable Maximum Likelihood Estimation via Sketching and Coresets

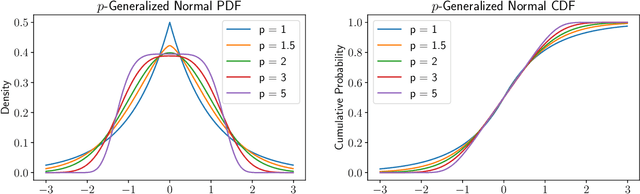
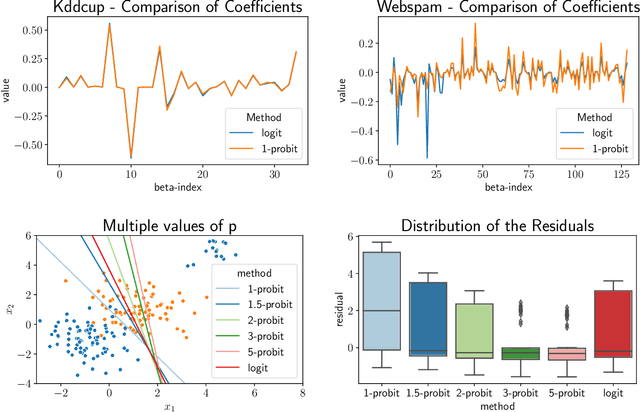
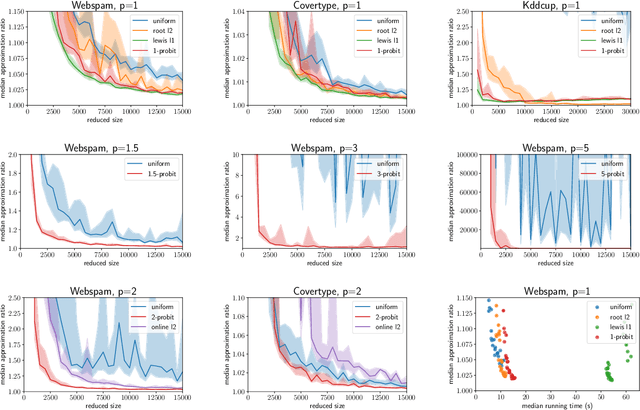
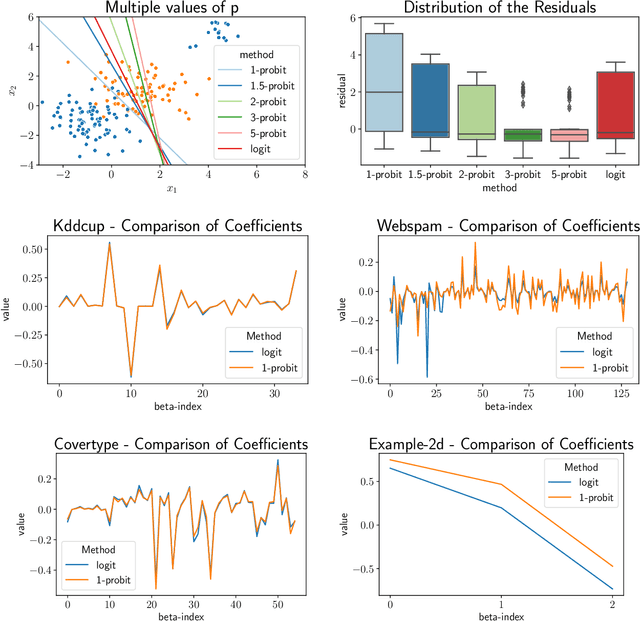
We study the $p$-generalized probit regression model, which is a generalized linear model for binary responses. It extends the standard probit model by replacing its link function, the standard normal cdf, by a $p$-generalized normal distribution for $p\in[1, \infty)$. The $p$-generalized normal distributions \citep{Sub23} are of special interest in statistical modeling because they fit much more flexibly to data. Their tail behavior can be controlled by choice of the parameter $p$, which influences the model's sensitivity to outliers. Special cases include the Laplace, the Gaussian, and the uniform distributions. We further show how the maximum likelihood estimator for $p$-generalized probit regression can be approximated efficiently up to a factor of $(1+\varepsilon)$ on large data by combining sketching techniques with importance subsampling to obtain a small data summary called coreset.

Binary Input Layer: Training of CNN models with binary input data

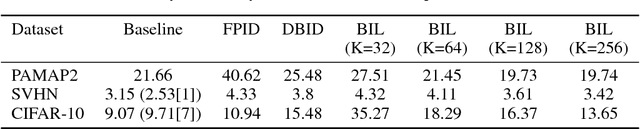
For the efficient execution of deep convolutional neural networks (CNN) on edge devices, various approaches have been presented which reduce the bit width of the network parameters down to 1 bit. Binarization of the first layer was always excluded, as it leads to a significant error increase. Here, we present the novel concept of binary input layer (BIL), which allows the usage of binary input data by learning bit specific binary weights. The concept is evaluated on three datasets (PAMAP2, SVHN, CIFAR-10). Our results show that this approach is in particular beneficial for multimodal datasets (PAMAP2) where it outperforms networks using full precision weights in the first layer by 1:92 percentage points (pp) while consuming only 2 % of the chip area.