Improved Learning via k-DTW: A Novel Dissimilarity Measure for Curves

This paper introduces $k$-Dynamic Time Warping ($k$-DTW), a novel dissimilarity measure for polygonal curves. $k$-DTW has stronger metric properties than Dynamic Time Warping (DTW) and is more robust to outliers than the Fr\'{e}chet distance, which are the two gold standards of dissimilarity measures for polygonal curves. We show interesting properties of $k$-DTW and give an exact algorithm as well as a $(1+\varepsilon)$-approximation algorithm for $k$-DTW by a parametric search for the $k$-th largest matched distance. We prove the first dimension-free learning bounds for curves and further learning theoretic results. $k$-DTW not only admits smaller sample size than DTW for the problem of learning the median of curves, where some factors depending on the curves' complexity $m$ are replaced by $k$, but we also show a surprising separation on the associated Rademacher and Gaussian complexities: $k$-DTW admits strictly smaller bounds than DTW, by a factor $\tilde\Omega(\sqrt{m})$ when $k\ll m$. We complement our theoretical findings with an experimental illustration of the benefits of using $k$-DTW for clustering and nearest neighbor classification.

Cutting Through Privacy: A Hyperplane-Based Data Reconstruction Attack in Federated Learning

Federated Learning (FL) enables collaborative training of machine learning models across distributed clients without sharing raw data, ostensibly preserving data privacy. Nevertheless, recent studies have revealed critical vulnerabilities in FL, showing that a malicious central server can manipulate model updates to reconstruct clients' private training data. Existing data reconstruction attacks have important limitations: they often rely on assumptions about the clients' data distribution or their efficiency significantly degrades when batch sizes exceed just a few tens of samples. In this work, we introduce a novel data reconstruction attack that overcomes these limitations. Our method leverages a new geometric perspective on fully connected layers to craft malicious model parameters, enabling the perfect recovery of arbitrarily large data batches in classification tasks without any prior knowledge of clients' data. Through extensive experiments on both image and tabular datasets, we demonstrate that our attack outperforms existing methods and achieves perfect reconstruction of data batches two orders of magnitude larger than the state of the art.

(k, l)-Medians Clustering of Trajectories Using Continuous Dynamic Time Warping

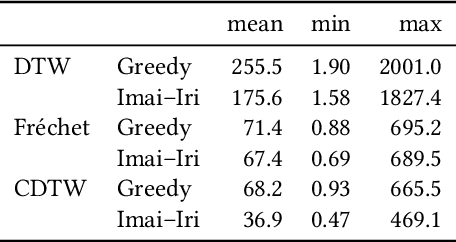
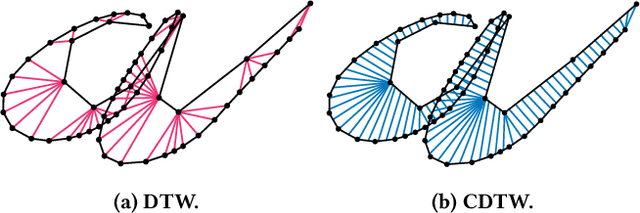
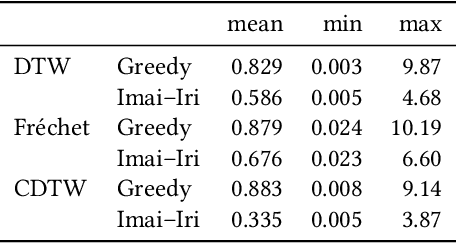
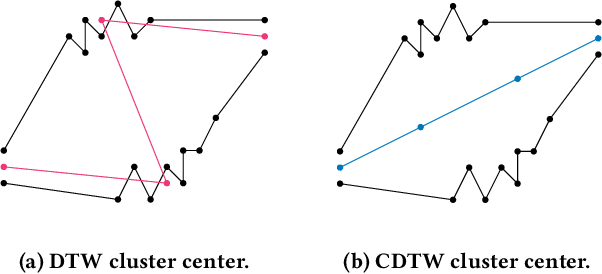
Due to the massively increasing amount of available geospatial data and the need to present it in an understandable way, clustering this data is more important than ever. As clusters might contain a large number of objects, having a representative for each cluster significantly facilitates understanding a clustering. Clustering methods relying on such representatives are called center-based. In this work we consider the problem of center-based clustering of trajectories. In this setting, the representative of a cluster is again a trajectory. To obtain a compact representation of the clusters and to avoid overfitting, we restrict the complexity of the representative trajectories by a parameter l. This restriction, however, makes discrete distance measures like dynamic time warping (DTW) less suited. There is recent work on center-based clustering of trajectories with a continuous distance measure, namely, the Fr\'echet distance. While the Fr\'echet distance allows for restriction of the center complexity, it can also be sensitive to outliers, whereas averaging-type distance measures, like DTW, are less so. To obtain a trajectory clustering algorithm that allows restricting center complexity and is more robust to outliers, we propose the usage of a continuous version of DTW as distance measure, which we call continuous dynamic time warping (CDTW). Our contribution is twofold: 1. To combat the lack of practical algorithms for CDTW, we develop an approximation algorithm that computes it. 2. We develop the first clustering algorithm under this distance measure and show a practical way to compute a center from a set of trajectories and subsequently iteratively improve it. To obtain insights into the results of clustering under CDTW on practical data, we conduct extensive experiments.