CIMRL: Combining IMitation and Reinforcement Learning for Safe Autonomous Driving

Modern approaches to autonomous driving rely heavily on learned components trained with large amounts of human driving data via imitation learning. However, these methods require large amounts of expensive data collection and even then face challenges with safely handling long-tail scenarios and compounding errors over time. At the same time, pure Reinforcement Learning (RL) methods can fail to learn performant policies in sparse, constrained, and challenging-to-define reward settings like driving. Both of these challenges make deploying purely cloned policies in safety critical applications like autonomous vehicles challenging. In this paper we propose Combining IMitation and Reinforcement Learning (CIMRL) approach - a framework that enables training driving policies in simulation through leveraging imitative motion priors and safety constraints. CIMRL does not require extensive reward specification and improves on the closed loop behavior of pure cloning methods. By combining RL and imitation, we demonstrate that our method achieves state-of-the-art results in closed loop simulation driving benchmarks.

Multi-Constraint Safe RL with Objective Suppression for Safety-Critical Applications

Safe reinforcement learning tasks with multiple constraints are a challenging domain despite being very common in the real world. To address this challenge, we propose Objective Suppression, a novel method that adaptively suppresses the task reward maximizing objectives according to a safety critic. We benchmark Objective Suppression in two multi-constraint safety domains, including an autonomous driving domain where any incorrect behavior can lead to disastrous consequences. Empirically, we demonstrate that our proposed method, when combined with existing safe RL algorithms, can match the task reward achieved by our baselines with significantly fewer constraint violations.

NUQ: Nonparametric Uncertainty Quantification for Deterministic Neural Networks

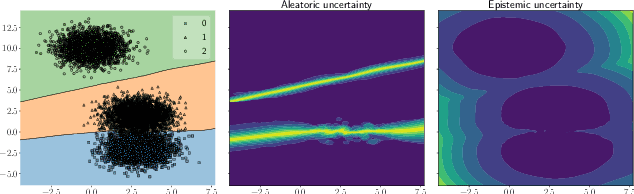
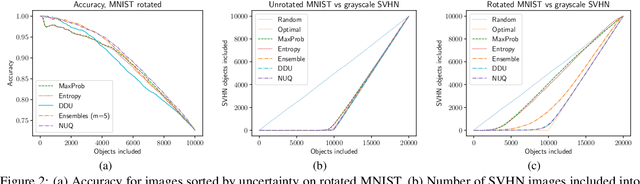
This paper proposes a fast and scalable method for uncertainty quantification of machine learning models' predictions. First, we show the principled way to measure the uncertainty of predictions for a classifier based on Nadaraya-Watson's nonparametric estimate of the conditional label distribution. Importantly, the approach allows to disentangle explicitly aleatoric and epistemic uncertainties. The resulting method works directly in the feature space. However, one can apply it to any neural network by considering an embedding of the data induced by the network. We demonstrate the strong performance of the method in uncertainty estimation tasks on a variety of real-world image datasets, such as MNIST, SVHN, CIFAR-100 and several versions of ImageNet.

Smoothed Embeddings for Certified Few-Shot Learning

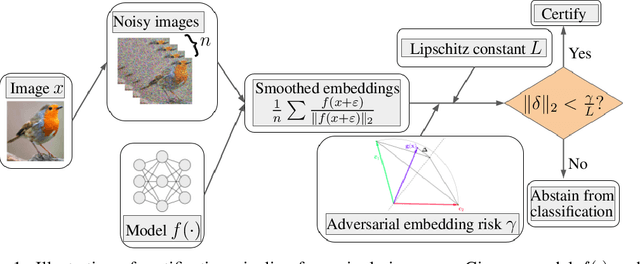
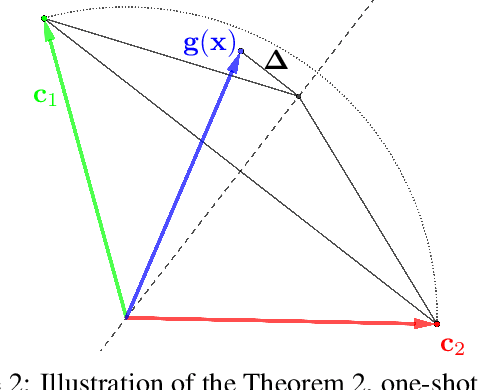
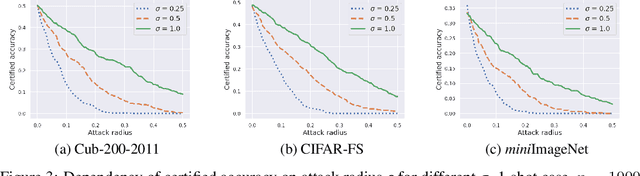
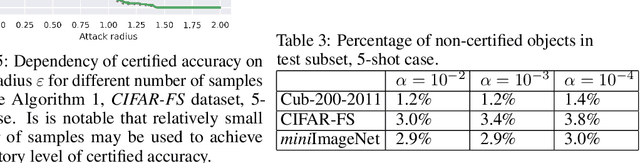
Randomized smoothing is considered to be the state-of-the-art provable defense against adversarial perturbations. However, it heavily exploits the fact that classifiers map input objects to class probabilities and do not focus on the ones that learn a metric space in which classification is performed by computing distances to embeddings of classes prototypes. In this work, we extend randomized smoothing to few-shot learning models that map inputs to normalized embeddings. We provide analysis of Lipschitz continuity of such models and derive robustness certificate against $\ell_2$-bounded perturbations that may be useful in few-shot learning scenarios. Our theoretical results are confirmed by experiments on different datasets.

Many Heads but One Brain: an Overview of Fusion Brain Challenge on AI Journey 2021

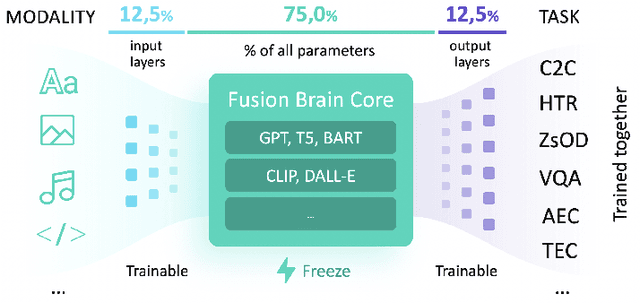
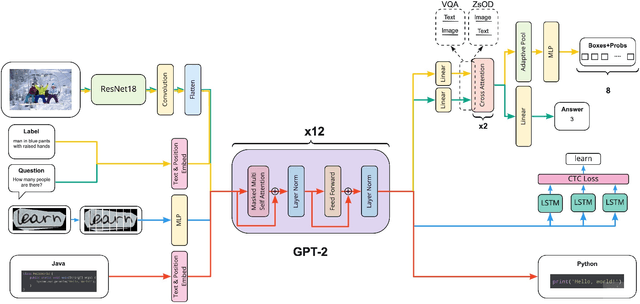
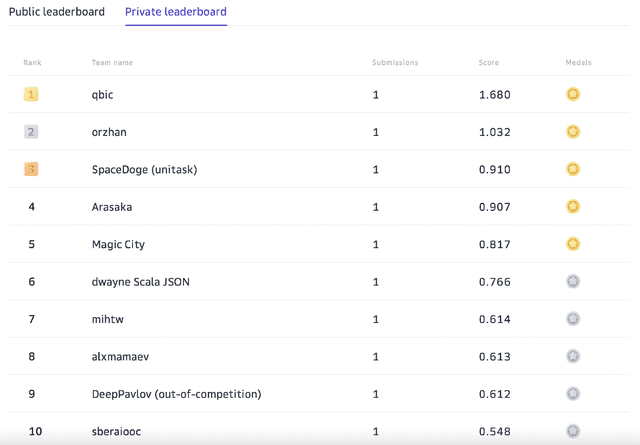
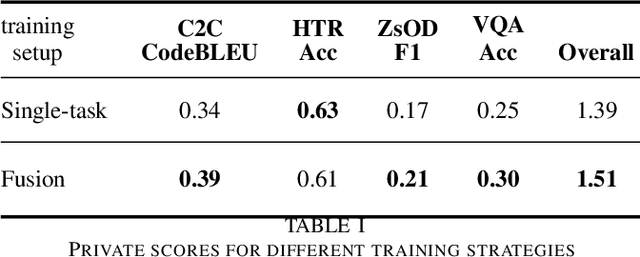
Supporting the current trend in the AI community, we propose the AI Journey 2021 Challenge called Fusion Brain which is targeted to make the universal architecture process different modalities (namely, images, texts, and code) and to solve multiple tasks for vision and language. The Fusion Brain Challenge https://github.com/sberbank-ai/fusion_brain_aij2021 combines the following specific tasks: Code2code Translation, Handwritten Text recognition, Zero-shot Object Detection, and Visual Question Answering. We have created datasets for each task to test the participants' submissions on it. Moreover, we have opened a new handwritten dataset in both Russian and English, which consists of 94,130 pairs of images and texts. The Russian part of the dataset is the largest Russian handwritten dataset in the world. We also propose the baseline solution and corresponding task-specific solutions as well as overall metrics.

CC-Cert: A Probabilistic Approach to Certify General Robustness of Neural Networks

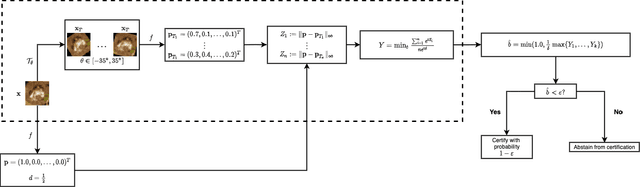
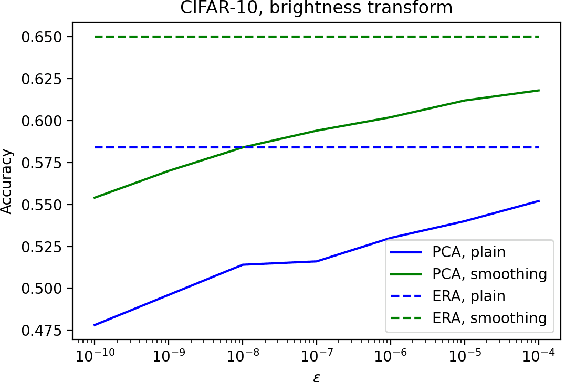
In safety-critical machine learning applications, it is crucial to defend models against adversarial attacks -- small modifications of the input that change the predictions. Besides rigorously studied $\ell_p$-bounded additive perturbations, recently proposed semantic perturbations (e.g. rotation, translation) raise a serious concern on deploying ML systems in real-world. Therefore, it is important to provide provable guarantees for deep learning models against semantically meaningful input transformations. In this paper, we propose a new universal probabilistic certification approach based on Chernoff-Cramer bounds that can be used in general attack settings. We estimate the probability of a model to fail if the attack is sampled from a certain distribution. Our theoretical findings are supported by experimental results on different datasets.

Manifold Hypothesis in Data Analysis: Double Geometrically-Probabilistic Approach to Manifold Dimension Estimation

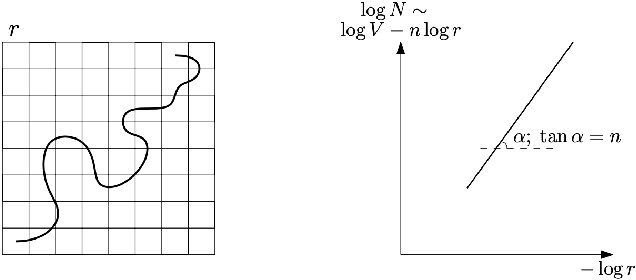
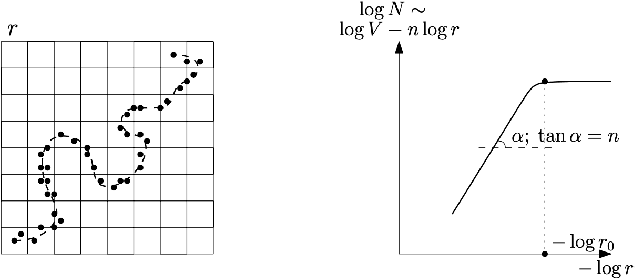
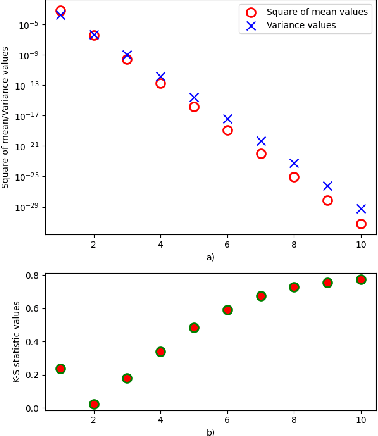
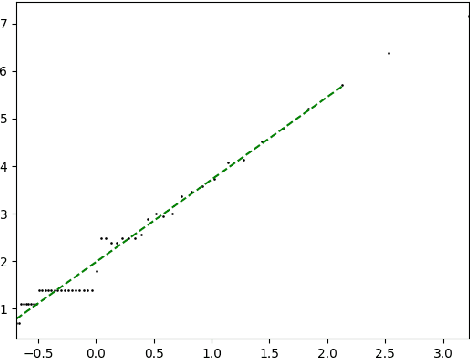
Manifold hypothesis states that data points in high-dimensional space actually lie in close vicinity of a manifold of much lower dimension. In many cases this hypothesis was empirically verified and used to enhance unsupervised and semi-supervised learning. Here we present new approach to manifold hypothesis checking and underlying manifold dimension estimation. In order to do it we use two very different methods simultaneously - one geometric, another probabilistic - and check whether they give the same result. Our geometrical method is a modification for sparse data of a well-known box-counting algorithm for Minkowski dimension calculation. The probabilistic method is new. Although it exploits standard nearest neighborhood distance, it is different from methods which were previously used in such situations. This method is robust, fast and includes special preliminary data transformation. Experiments on real datasets show that the suggested approach based on two methods combination is powerful and effective.

Darker than Black-Box: Face Reconstruction from Similarity Queries

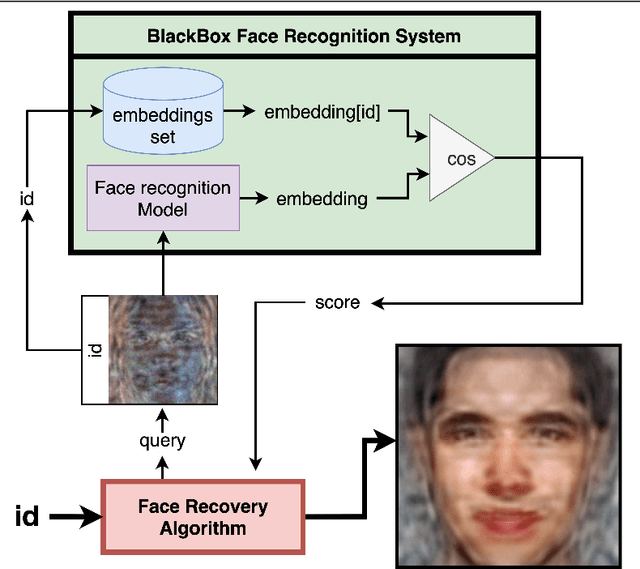
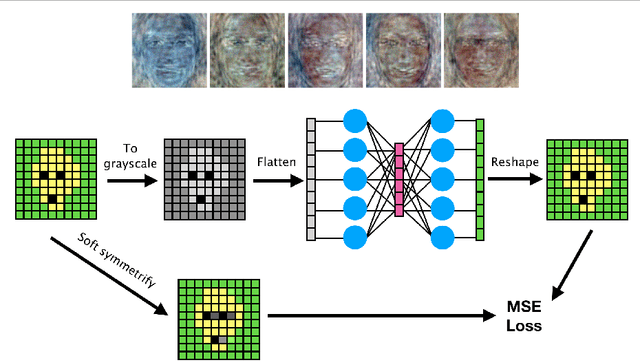
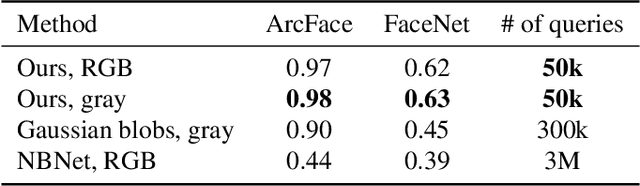
Several methods for inversion of face recognition models were recently presented, attempting to reconstruct a face from deep templates. Although some of these approaches work in a black-box setup using only face embeddings, usually, on the end-user side, only similarity scores are provided. Therefore, these algorithms are inapplicable in such scenarios. We propose a novel approach that allows reconstructing the face querying only similarity scores of the black-box model. While our algorithm operates in a more general setup, experiments show that it is query efficient and outperforms the existing methods.

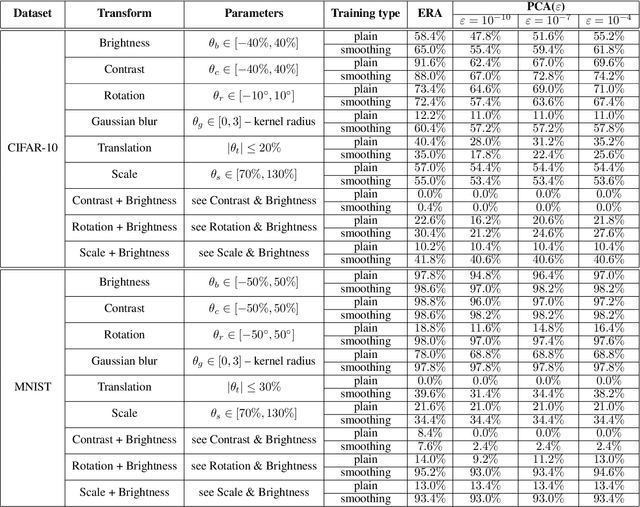
Certified Robustness via Randomized Smoothing over Multiplicative Parameters

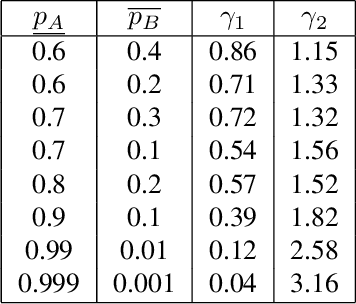
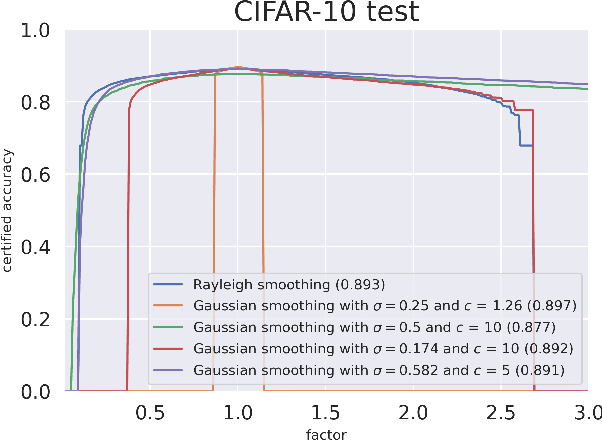
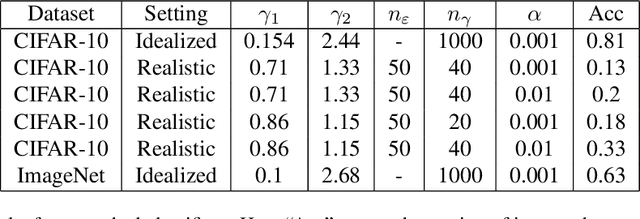
We propose a novel approach of randomized smoothing over multiplicative parameters. Using this method we construct certifiably robust classifiers with respect to a gamma-correction perturbation and compare the result with classifiers obtained via Gaussian smoothing. To the best of our knowledge it is the first work concerning certified robustness against the multiplicative gamma-correction transformation.

MDMMT: Multidomain Multimodal Transformer for Video Retrieval

We present a new state-of-the-art on the text to video retrieval task on MSRVTT and LSMDC benchmarks where our model outperforms all previous solutions by a large margin. Moreover, state-of-the-art results are achieved with a single model on two datasets without finetuning. This multidomain generalisation is achieved by a proper combination of different video caption datasets. We show that training on different datasets can improve test results of each other. Additionally we check intersection between many popular datasets and found that MSRVTT has a significant overlap between the test and the train parts, and the same situation is observed for ActivityNet.