On Path to Multimodal Historical Reasoning: HistBench and HistAgent

Recent advances in large language models (LLMs) have led to remarkable progress across domains, yet their capabilities in the humanities, particularly history, remain underexplored. Historical reasoning poses unique challenges for AI, involving multimodal source interpretation, temporal inference, and cross-linguistic analysis. While general-purpose agents perform well on many existing benchmarks, they lack the domain-specific expertise required to engage with historical materials and questions. To address this gap, we introduce HistBench, a new benchmark of 414 high-quality questions designed to evaluate AI's capacity for historical reasoning and authored by more than 40 expert contributors. The tasks span a wide range of historical problems-from factual retrieval based on primary sources to interpretive analysis of manuscripts and images, to interdisciplinary challenges involving archaeology, linguistics, or cultural history. Furthermore, the benchmark dataset spans 29 ancient and modern languages and covers a wide range of historical periods and world regions. Finding the poor performance of LLMs and other agents on HistBench, we further present HistAgent, a history-specific agent equipped with carefully designed tools for OCR, translation, archival search, and image understanding in History. On HistBench, HistAgent based on GPT-4o achieves an accuracy of 27.54% pass@1 and 36.47% pass@2, significantly outperforming LLMs with online search and generalist agents, including GPT-4o (18.60%), DeepSeek-R1(14.49%) and Open Deep Research-smolagents(20.29% pass@1 and 25.12% pass@2). These results highlight the limitations of existing LLMs and generalist agents and demonstrate the advantages of HistAgent for historical reasoning.

Pure Component Property Estimation Framework Using Explainable Machine Learning Methods

Accurate prediction of pure component physiochemical properties is crucial for process integration, multiscale modeling, and optimization. In this work, an enhanced framework for pure component property prediction by using explainable machine learning methods is proposed. In this framework, the molecular representation method based on the connectivity matrix effectively considers atomic bonding relationships to automatically generate features. The supervised machine learning model random forest is applied for feature ranking and pooling. The adjusted R2 is introduced to penalize the inclusion of additional features, providing an assessment of the true contribution of features. The prediction results for normal boiling point (Tb), liquid molar volume, critical temperature (Tc) and critical pressure (Pc) obtained using Artificial Neural Network and Gaussian Process Regression models confirm the accuracy of the molecular representation method. Comparison with GC based models shows that the root-mean-square error on the test set can be reduced by up to 83.8%. To enhance the interpretability of the model, a feature analysis method based on Shapley values is employed to determine the contribution of each feature to the property predictions. The results indicate that using the feature pooling method reduces the number of features from 13316 to 100 without compromising model accuracy. The feature analysis results for Tb, Tc, and Pc confirms that different molecular properties are influenced by different structural features, aligning with mechanistic interpretations. In conclusion, the proposed framework is demonstrated to be feasible and provides a solid foundation for mixture component reconstruction and process integration modelling.

A High-Dynamic-Range Digital RF-Over-Fiber Link for MRI Receive Coils Using Delta-Sigma Modulation

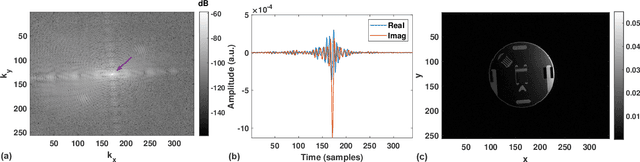
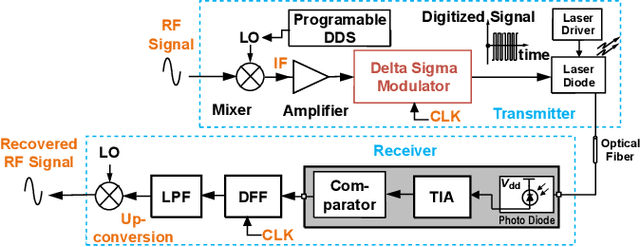
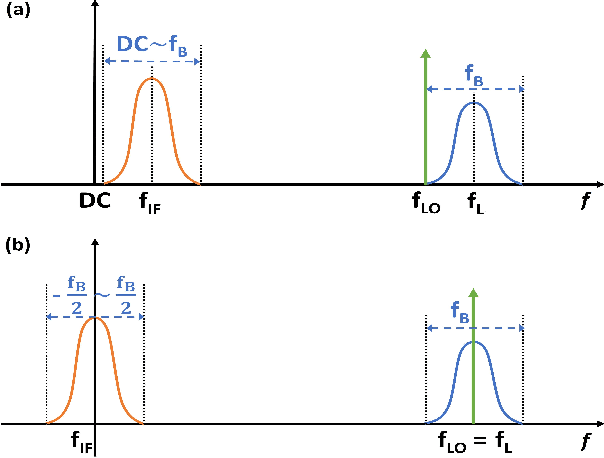
The coaxial cables commonly used to connect RF coil arrays with the control console of an MRI scanner are susceptible to electromagnetic coupling. As the number of RF channel increases, such coupling could result in severe heating and pose a safety concern. Non-conductive transmission solutions based on fiber-optic cables are considered to be one of the alternatives, but are limited by the high dynamic range ($>80$~dB) of typical MRI signals. A new digital fiber-optic transmission system based on delta-sigma modulation (DSM) is developed to address this problem. A DSM-based optical link is prototyped using off-the-shelf components and bench-tested at different signal oversampling rates (OSR). An end-to-end dynamic range (DR) of 81~dB, which is sufficient for typical MRI signals, is obtained over a bandwidth of 200~kHz, which corresponds to $OSR=50$. A fully-integrated custom fourth-order continuous-time DSM (CT-DSM) is designed in 180~nm CMOS technology to enable transmission of full-bandwidth MRI signals (up to 1~MHz) with adequate DR. Initial electrical test results from this custom chip are also presented.

Combinatorial Losses through Generalized Gradients of Integer Linear Programs

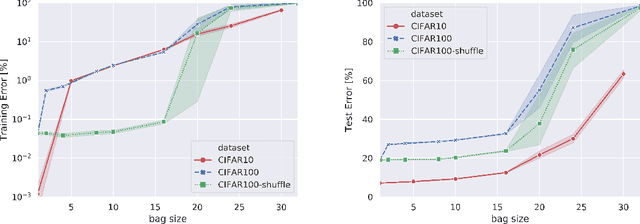
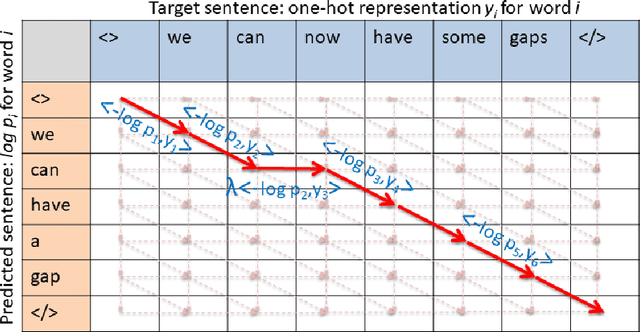
When samples have internal structure, we often see a mismatch between the objective optimized during training and the model's goal during inference. For example, in sequence-to-sequence modeling we are interested in high-quality translated sentences, but training typically uses maximum likelihood at the word level. Learning to recognize individual faces from group photos, each captioned with the correct but unordered list of people in it, is another example where a mismatch between training and inference objectives occurs. In both cases, the natural training-time loss would involve a combinatorial problem -- dynamic programming-based global sequence alignment and weighted bipartite graph matching, respectively -- but solutions to combinatorial problems are not differentiable with respect to their input parameters, so surrogate, differentiable losses are used instead. Here, we show how to perform gradient descent over combinatorial optimization algorithms that involve continuous parameters, for example edge weights, and can be efficiently expressed as integer, linear, or mixed-integer linear programs. We demonstrate usefulness of gradient descent over combinatorial optimization in sequence-to-sequence modeling using differentiable encoder-decoder architecture with softmax or Gumbel-softmax, and in weakly supervised learning involving a convolutional, residual feed-forward network for image classification.

Approximation Capabilities of Neural Ordinary Differential Equations

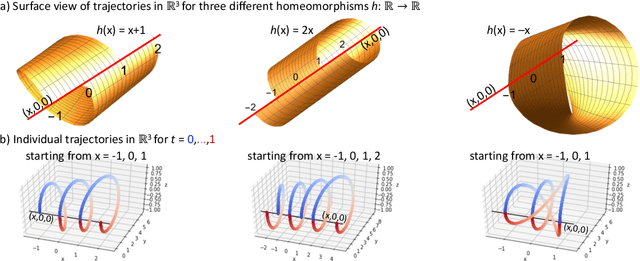
Neural Ordinary Differential Equations have been recently proposed as an infinite-depth generalization of residual networks. Neural ODEs provide out-of-the-box invertibility of the mapping realized by the neural network, and can lead to networks that are more efficient in terms of computational time and parameter space. Here, we show that a Neural ODE operating on a space with dimensionality increased by one compared to the input dimension is a universal approximator for the space of continuous functions, at the cost of loosing invertibility. We then turn our focus to invertible mappings, and we prove that any homeomorphism on a $p$-dimensional Euclidean space can be approximated by a Neural ODE operating on a $(2p+1)$-dimensional Euclidean space.