Deceptive Sequential Decision-Making via Regularized Policy Optimization

Autonomous systems are increasingly expected to operate in the presence of adversaries, though an adversary may infer sensitive information simply by observing a system, without even needing to interact with it. Therefore, in this work we present a deceptive decision-making framework that not only conceals sensitive information, but in fact actively misleads adversaries about it. We model autonomous systems as Markov decision processes, and we consider adversaries that attempt to infer their reward functions using inverse reinforcement learning. To counter such efforts, we present two regularization strategies for policy synthesis problems that actively deceive an adversary about a system's underlying rewards. The first form of deception is ``diversionary'', and it leads an adversary to draw any false conclusion about what the system's reward function is. The second form of deception is ``targeted'', and it leads an adversary to draw a specific false conclusion about what the system's reward function is. We then show how each form of deception can be implemented in policy optimization problems, and we analytically bound the loss in total accumulated reward that is induced by deception. Next, we evaluate these developments in a multi-agent sequential decision-making problem with one real agent and multiple decoys. We show that diversionary deception can cause the adversary to believe that the most important agent is the least important, while attaining a total accumulated reward that is $98.83\%$ of its optimal, non-deceptive value. Similarly, we show that targeted deception can make any decoy appear to be the most important agent, while still attaining a total accumulated reward that is $99.25\%$ of its optimal, non-deceptive value.

Logical Specifications-guided Dynamic Task Sampling for Reinforcement Learning Agents

Reinforcement Learning (RL) has made significant strides in enabling artificial agents to learn diverse behaviors. However, learning an effective policy often requires a large number of environment interactions. To mitigate sample complexity issues, recent approaches have used high-level task specifications, such as Linear Temporal Logic (LTL$_f$) formulas or Reward Machines (RM), to guide the learning progress of the agent. In this work, we propose a novel approach, called Logical Specifications-guided Dynamic Task Sampling (LSTS), that learns a set of RL policies to guide an agent from an initial state to a goal state based on a high-level task specification, while minimizing the number of environmental interactions. Unlike previous work, LSTS does not assume information about the environment dynamics or the Reward Machine, and dynamically samples promising tasks that lead to successful goal policies. We evaluate LSTS on a gridworld and show that it achieves improved time-to-threshold performance on complex sequential decision-making problems compared to state-of-the-art RM and Automaton-guided RL baselines, such as Q-Learning for Reward Machines and Compositional RL from logical Specifications (DIRL). Moreover, we demonstrate that our method outperforms RM and Automaton-guided RL baselines in terms of sample-efficiency, both in a partially observable robotic task and in a continuous control robotic manipulation task.

Automaton-Guided Curriculum Generation for Reinforcement Learning Agents

Despite advances in Reinforcement Learning, many sequential decision making tasks remain prohibitively expensive and impractical to learn. Recently, approaches that automatically generate reward functions from logical task specifications have been proposed to mitigate this issue; however, they scale poorly on long-horizon tasks (i.e., tasks where the agent needs to perform a series of correct actions to reach the goal state, considering future transitions while choosing an action). Employing a curriculum (a sequence of increasingly complex tasks) further improves the learning speed of the agent by sequencing intermediate tasks suited to the learning capacity of the agent. However, generating curricula from the logical specification still remains an unsolved problem. To this end, we propose AGCL, Automaton-guided Curriculum Learning, a novel method for automatically generating curricula for the target task in the form of Directed Acyclic Graphs (DAGs). AGCL encodes the specification in the form of a deterministic finite automaton (DFA), and then uses the DFA along with the Object-Oriented MDP (OOMDP) representation to generate a curriculum as a DAG, where the vertices correspond to tasks, and edges correspond to the direction of knowledge transfer. Experiments in gridworld and physics-based simulated robotics domains show that the curricula produced by AGCL achieve improved time-to-threshold performance on a complex sequential decision-making problem relative to state-of-the-art curriculum learning (e.g, teacher-student, self-play) and automaton-guided reinforcement learning baselines (e.g, Q-Learning for Reward Machines). Further, we demonstrate that AGCL performs well even in the presence of noise in the task's OOMDP description, and also when distractor objects are present that are not modeled in the logical specification of the tasks' objectives.

Neural Decoder for Topological Codes using Pseudo-Inverse of Parity Check Matrix

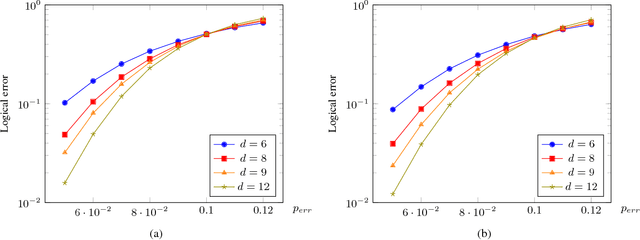
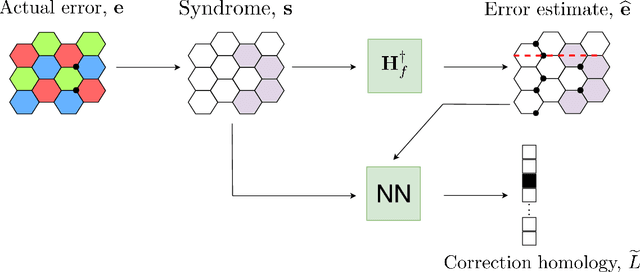
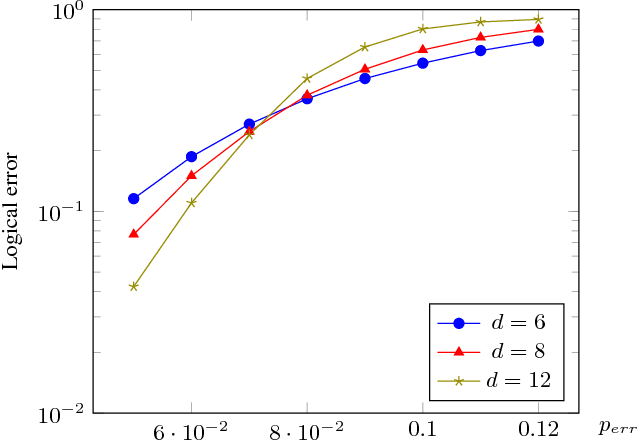
Recent developments in the field of deep learning have motivated many researchers to apply these methods to problems in quantum information. Torlai and Melko first proposed a decoder for surface codes based on neural networks. Since then, many other researchers have applied neural networks to study a variety of problems in the context of decoding. An important development in this regard was due to Varsamopoulos et al. who proposed a two-step decoder using neural networks. Subsequent work of Maskara et al. used the same concept for decoding for various noise models. We propose a similar two-step neural decoder using inverse parity-check matrix for topological color codes. We show that it outperforms the state-of-the-art performance of non-neural decoders for independent Pauli errors noise model on a 2D hexagonal color code. Our final decoder is independent of the noise model and achieves a threshold of $10 \%$. Our result is comparable to the recent work on neural decoder for quantum error correction by Maskara et al.. It appears that our decoder has significant advantages with respect to training cost and complexity of the network for higher lengths when compared to that of Maskara et al.. Our proposed method can also be extended to arbitrary dimension and other stabilizer codes.