Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning

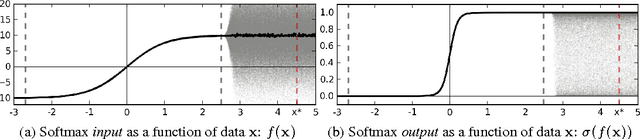
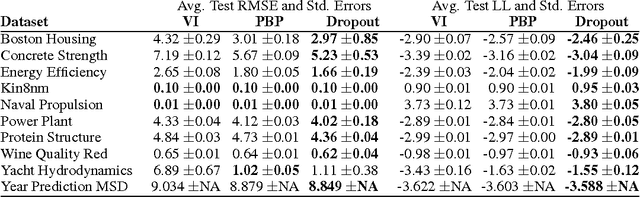
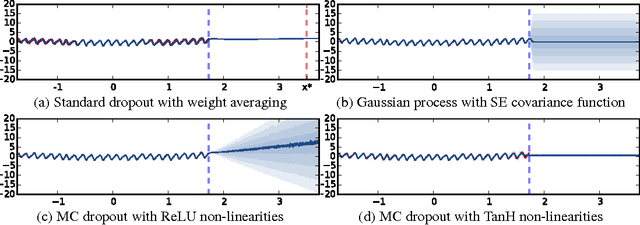
Deep learning tools have gained tremendous attention in applied machine learning. However such tools for regression and classification do not capture model uncertainty. In comparison, Bayesian models offer a mathematically grounded framework to reason about model uncertainty, but usually come with a prohibitive computational cost. In this paper we develop a new theoretical framework casting dropout training in deep neural networks (NNs) as approximate Bayesian inference in deep Gaussian processes. A direct result of this theory gives us tools to model uncertainty with dropout NNs -- extracting information from existing models that has been thrown away so far. This mitigates the problem of representing uncertainty in deep learning without sacrificing either computational complexity or test accuracy. We perform an extensive study of the properties of dropout's uncertainty. Various network architectures and non-linearities are assessed on tasks of regression and classification, using MNIST as an example. We show a considerable improvement in predictive log-likelihood and RMSE compared to existing state-of-the-art methods, and finish by using dropout's uncertainty in deep reinforcement learning.

A General Framework for Constrained Bayesian Optimization using Information-based Search

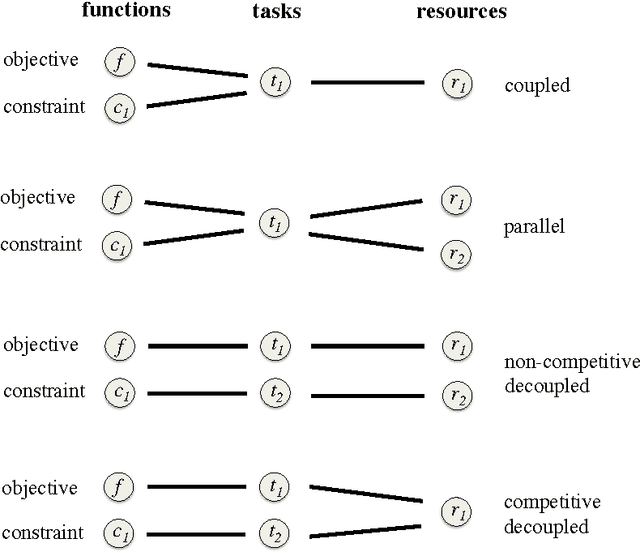
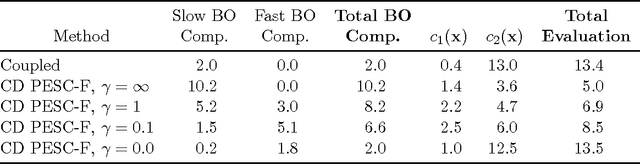
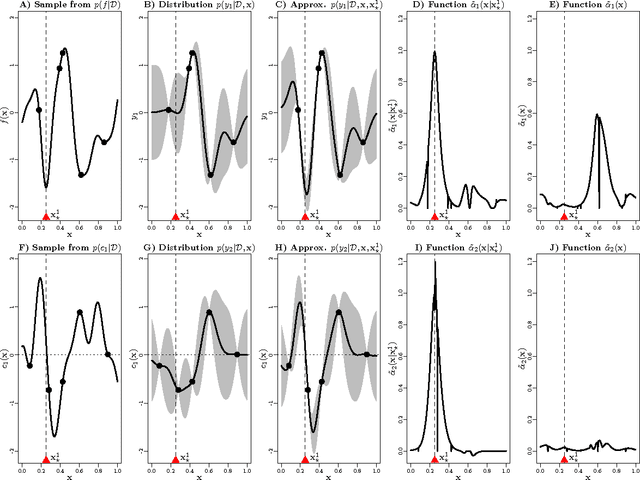
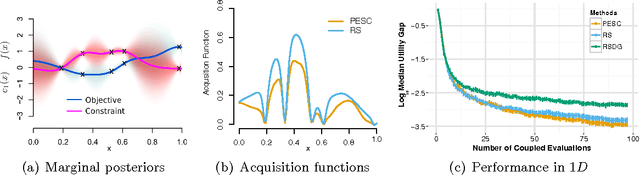
We present an information-theoretic framework for solving global black-box optimization problems that also have black-box constraints. Of particular interest to us is to efficiently solve problems with decoupled constraints, in which subsets of the objective and constraint functions may be evaluated independently. For example, when the objective is evaluated on a CPU and the constraints are evaluated independently on a GPU. These problems require an acquisition function that can be separated into the contributions of the individual function evaluations. We develop one such acquisition function and call it Predictive Entropy Search with Constraints (PESC). PESC is an approximation to the expected information gain criterion and it compares favorably to alternative approaches based on improvement in several synthetic and real-world problems. In addition to this, we consider problems with a mix of functions that are fast and slow to evaluate. These problems require balancing the amount of time spent in the meta-computation of PESC and in the actual evaluation of the target objective. We take a bounded rationality approach and develop partial update for PESC which trades off accuracy against speed. We then propose a method for adaptively switching between the partial and full updates for PESC. This allows us to interpolate between versions of PESC that are efficient in terms of function evaluations and those that are efficient in terms of wall-clock time. Overall, we demonstrate that PESC is an effective algorithm that provides a promising direction towards a unified solution for constrained Bayesian optimization.

A study of the effect of JPG compression on adversarial images

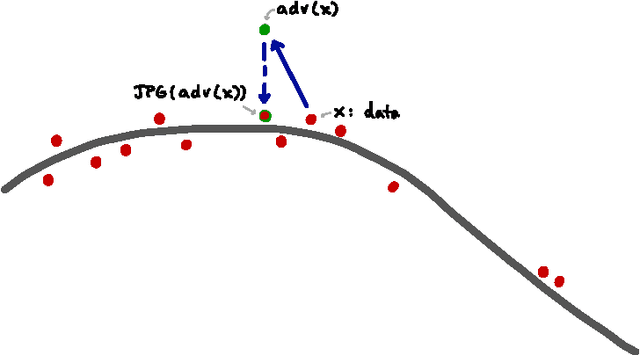
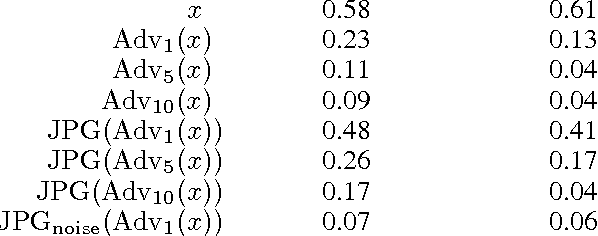
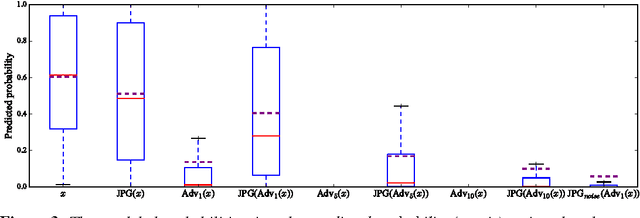
Neural network image classifiers are known to be vulnerable to adversarial images, i.e., natural images which have been modified by an adversarial perturbation specifically designed to be imperceptible to humans yet fool the classifier. Not only can adversarial images be generated easily, but these images will often be adversarial for networks trained on disjoint subsets of data or with different architectures. Adversarial images represent a potential security risk as well as a serious machine learning challenge---it is clear that vulnerable neural networks perceive images very differently from humans. Noting that virtually every image classification data set is composed of JPG images, we evaluate the effect of JPG compression on the classification of adversarial images. For Fast-Gradient-Sign perturbations of small magnitude, we found that JPG compression often reverses the drop in classification accuracy to a large extent, but not always. As the magnitude of the perturbations increases, JPG recompression alone is insufficient to reverse the effect.

Avoiding pathologies in very deep networks

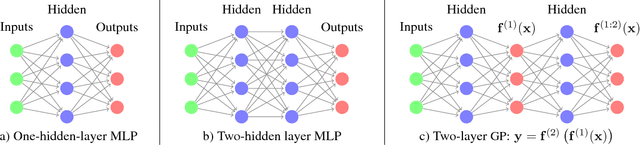
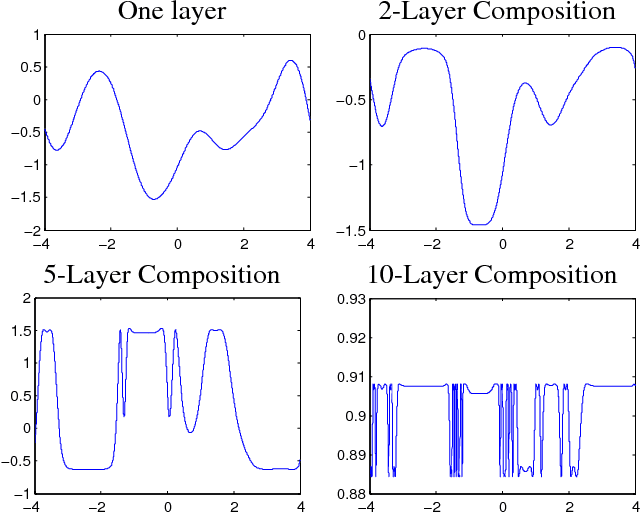
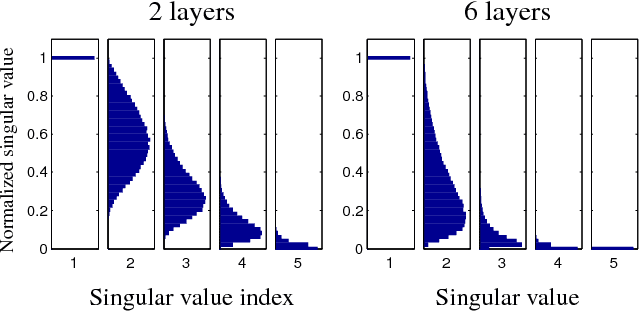
Choosing appropriate architectures and regularization strategies for deep networks is crucial to good predictive performance. To shed light on this problem, we analyze the analogous problem of constructing useful priors on compositions of functions. Specifically, we study the deep Gaussian process, a type of infinitely-wide, deep neural network. We show that in standard architectures, the representational capacity of the network tends to capture fewer degrees of freedom as the number of layers increases, retaining only a single degree of freedom in the limit. We propose an alternate network architecture which does not suffer from this pathology. We also examine deep covariance functions, obtained by composing infinitely many feature transforms. Lastly, we characterize the class of models obtained by performing dropout on Gaussian processes.

The Mondrian Kernel

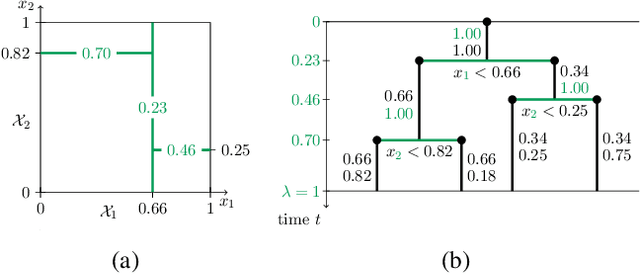
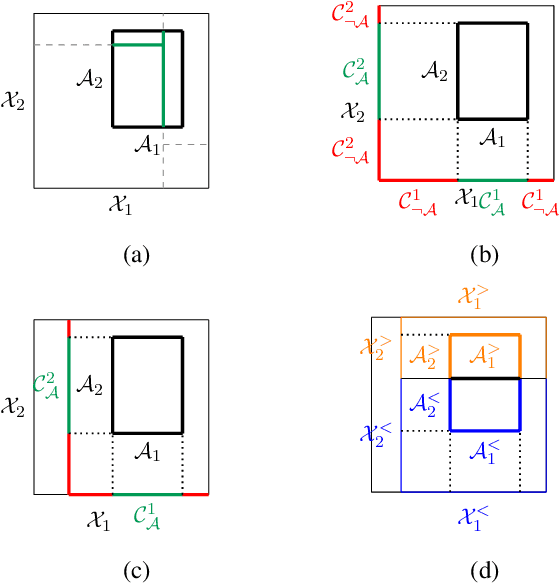
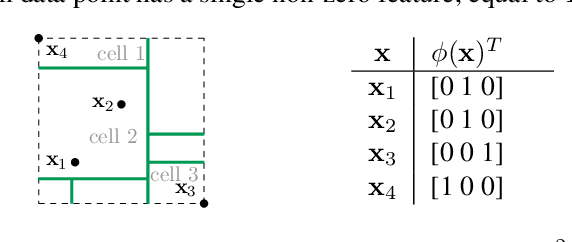
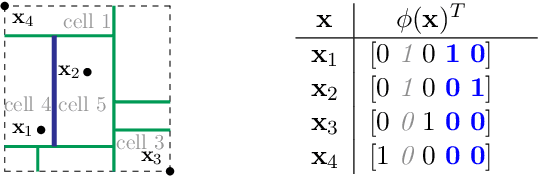
We introduce the Mondrian kernel, a fast random feature approximation to the Laplace kernel. It is suitable for both batch and online learning, and admits a fast kernel-width-selection procedure as the random features can be re-used efficiently for all kernel widths. The features are constructed by sampling trees via a Mondrian process [Roy and Teh, 2009], and we highlight the connection to Mondrian forests [Lakshminarayanan et al., 2014], where trees are also sampled via a Mondrian process, but fit independently. This link provides a new insight into the relationship between kernel methods and random forests.

Dropout as a Bayesian Approximation: Appendix

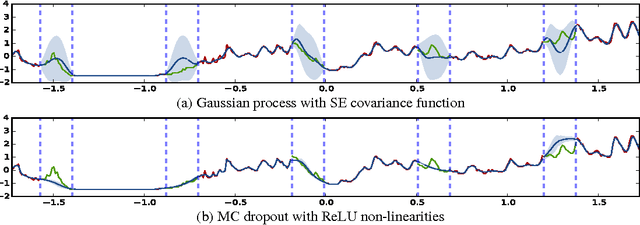
We show that a neural network with arbitrary depth and non-linearities, with dropout applied before every weight layer, is mathematically equivalent to an approximation to a well known Bayesian model. This interpretation might offer an explanation to some of dropout's key properties, such as its robustness to over-fitting. Our interpretation allows us to reason about uncertainty in deep learning, and allows the introduction of the Bayesian machinery into existing deep learning frameworks in a principled way. This document is an appendix for the main paper "Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning" by Gal and Ghahramani, 2015.

Distributed Flexible Nonlinear Tensor Factorization

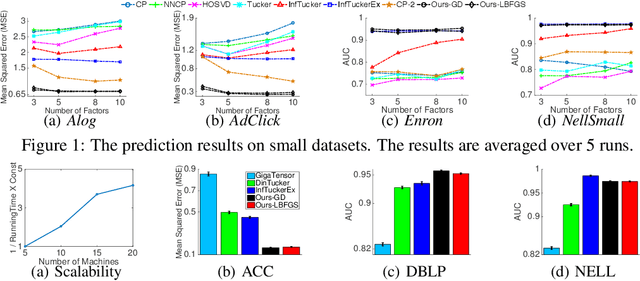
Tensor factorization is a powerful tool to analyse multi-way data. Compared with traditional multi-linear methods, nonlinear tensor factorization models are capable of capturing more complex relationships in the data. However, they are computationally expensive and may suffer severe learning bias in case of extreme data sparsity. To overcome these limitations, in this paper we propose a distributed, flexible nonlinear tensor factorization model. Our model can effectively avoid the expensive computations and structural restrictions of the Kronecker-product in existing TGP formulations, allowing an arbitrary subset of tensorial entries to be selected to contribute to the training. At the same time, we derive a tractable and tight variational evidence lower bound (ELBO) that enables highly decoupled, parallel computations and high-quality inference. Based on the new bound, we develop a distributed inference algorithm in the MapReduce framework, which is key-value-free and can fully exploit the memory cache mechanism in fast MapReduce systems such as SPARK. Experimental results fully demonstrate the advantages of our method over several state-of-the-art approaches, in terms of both predictive performance and computational efficiency. Moreover, our approach shows a promising potential in the application of Click-Through-Rate (CTR) prediction for online advertising.

Scalable Discrete Sampling as a Multi-Armed Bandit Problem

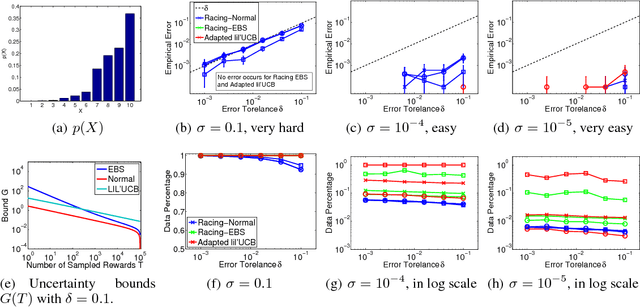
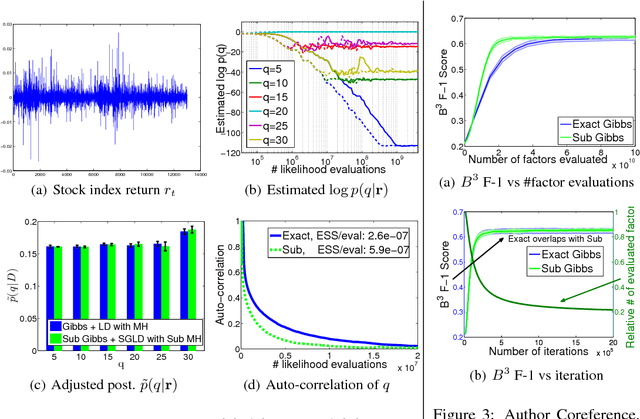
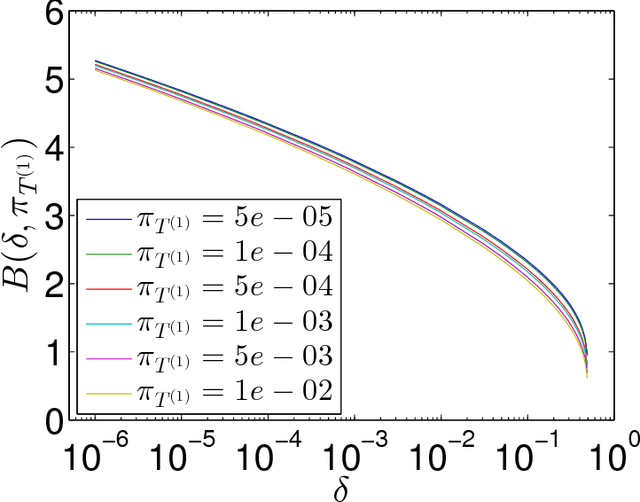
Drawing a sample from a discrete distribution is one of the building components for Monte Carlo methods. Like other sampling algorithms, discrete sampling suffers from the high computational burden in large-scale inference problems. We study the problem of sampling a discrete random variable with a high degree of dependency that is typical in large-scale Bayesian inference and graphical models, and propose an efficient approximate solution with a subsampling approach. We make a novel connection between the discrete sampling and Multi-Armed Bandits problems with a finite reward population and provide three algorithms with theoretical guarantees. Empirical evaluations show the robustness and efficiency of the approximate algorithms in both synthetic and real-world large-scale problems.

Linear Dimensionality Reduction: Survey, Insights, and Generalizations

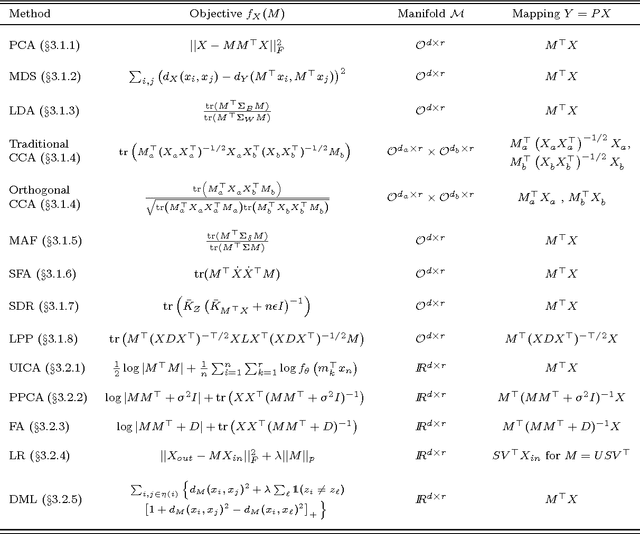
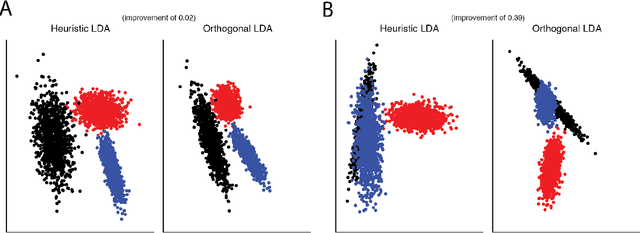
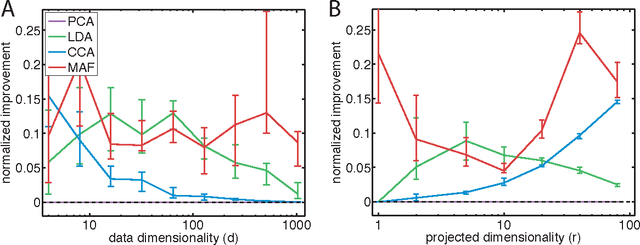
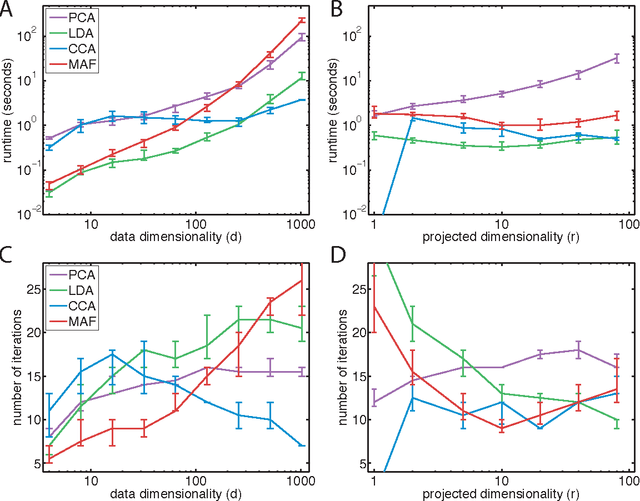
Linear dimensionality reduction methods are a cornerstone of analyzing high dimensional data, due to their simple geometric interpretations and typically attractive computational properties. These methods capture many data features of interest, such as covariance, dynamical structure, correlation between data sets, input-output relationships, and margin between data classes. Methods have been developed with a variety of names and motivations in many fields, and perhaps as a result the connections between all these methods have not been highlighted. Here we survey methods from this disparate literature as optimization programs over matrix manifolds. We discuss principal component analysis, factor analysis, linear multidimensional scaling, Fisher's linear discriminant analysis, canonical correlations analysis, maximum autocorrelation factors, slow feature analysis, sufficient dimensionality reduction, undercomplete independent component analysis, linear regression, distance metric learning, and more. This optimization framework gives insight to some rarely discussed shortcomings of well-known methods, such as the suboptimality of certain eigenvector solutions. Modern techniques for optimization over matrix manifolds enable a generic linear dimensionality reduction solver, which accepts as input data and an objective to be optimized, and returns, as output, an optimal low-dimensional projection of the data. This simple optimization framework further allows straightforward generalizations and novel variants of classical methods, which we demonstrate here by creating an orthogonal-projection canonical correlations analysis. More broadly, this survey and generic solver suggest that linear dimensionality reduction can move toward becoming a blackbox, objective-agnostic numerical technology.

Bayesian Convolutional Neural Networks with Bernoulli Approximate Variational Inference

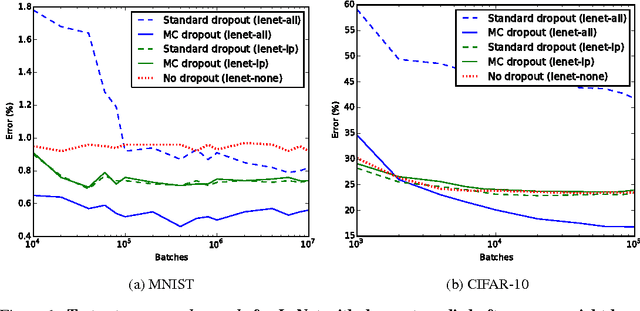
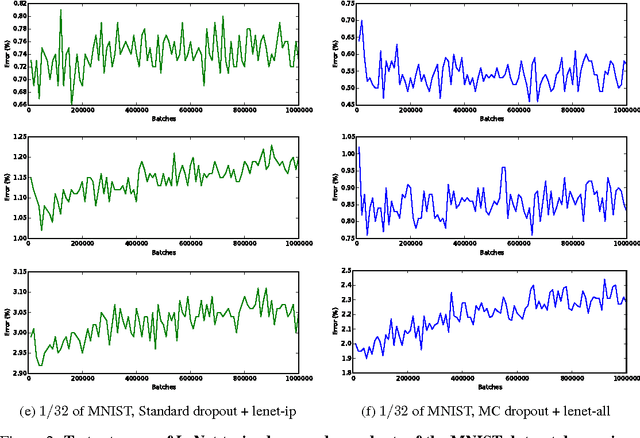
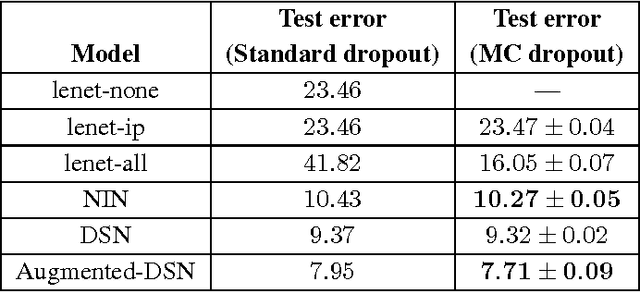
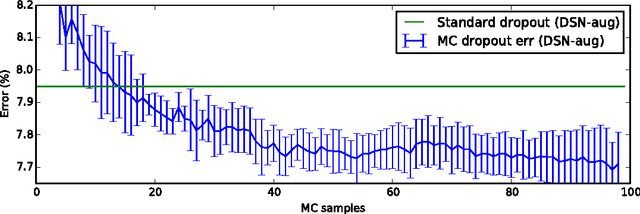
Convolutional neural networks (CNNs) work well on large datasets. But labelled data is hard to collect, and in some applications larger amounts of data are not available. The problem then is how to use CNNs with small data -- as CNNs overfit quickly. We present an efficient Bayesian CNN, offering better robustness to over-fitting on small data than traditional approaches. This is by placing a probability distribution over the CNN's kernels. We approximate our model's intractable posterior with Bernoulli variational distributions, requiring no additional model parameters. On the theoretical side, we cast dropout network training as approximate inference in Bayesian neural networks. This allows us to implement our model using existing tools in deep learning with no increase in time complexity, while highlighting a negative result in the field. We show a considerable improvement in classification accuracy compared to standard techniques and improve on published state-of-the-art results for CIFAR-10.