MixRea: Benchmarking Explicit-Implicit Reasoning in Large Language Models

Large language models (LLMs) are increasingly integrated into high-stakes decision-making. Inspired by the theory of \emph{inattentional blindness} in human cognition, we investigate whether LLMs, trained on human-preferred corpora that embed attentional biases, exhibit a similar limitation: \emph{failing to attend to subtle yet important contextual cues under explicit task instructions}. To evaluate this, we introduce the task of \textbf{explicit-implicit reasoning} and present \textbf{MixRea}, a benchmark of 2,246 multiple-choice questions across 9 reasoning types with varying distributions of explicit and implicit information. Evaluation of 21 advanced LLMs shows that even the best-performing reasoning model (Gemini 2.5 Pro) achieves only 42.8\% consistency, revealing widespread inattentional blindness. To mitigate this, we propose \textbf{Potential Relation Completion Prompting (PRCP)}, a prompting method that improves reasoning by recovering overlooked causal relations. Further analysis shows that this limitation persists across diverse multi-source reasoning tasks, highlighting the need for more cognitively aligned models.

Utility-Oriented Visual Evidence Selection for Multimodal Retrieval-Augmented Generation

Visual evidence selection is a critical component of multimodal retrieval-augmented generation (RAG), yet existing methods typically rely on semantic relevance or surface-level similarity, which are often misaligned with the actual utility of visual evidence for downstream reasoning. We reformulate multimodal evidence selection from an information-theoretic perspective by defining evidence utility as the information gain induced on a model's output distribution. To overcome the intractability of answer-space optimization, we introduce a latent notion of evidence helpfulness and theoretically show that, under mild assumptions, ranking evidence by information gain on this latent variable is equivalent to answer-space utility. We further propose a training-free, surrogate-accelerated framework that efficiently estimates evidence utility using lightweight multimodal models. Experiments on MRAG-Bench and Visual-RAG across multiple model families demonstrate that our method consistently outperforms state-of-the-art RAG baselines while achieving substantial reductions in computational cost.

Super-Resolution and Denoising of Corneal B-Scan OCT Imaging Using Diffusion Model Plug-and-Play Priors

Optical coherence tomography (OCT) is pivotal in corneal imaging for both surgical planning and diagnosis. However, high-speed acquisitions often degrade spatial resolution and increase speckle noise, posing challenges for accurate interpretation. We propose an advanced super-resolution framework leveraging diffusion model plug-and-play (PnP) priors to achieve 4x spatial resolution enhancement alongside effective denoising of OCT Bscan images. Our approach formulates reconstruction as a principled Bayesian inverse problem, combining Markov chain Monte Carlo sampling with pretrained generative priors to enforce anatomical consistency. We comprehensively validate the framework using \emph{in vivo} fisheye corneal datasets, to assess robustness and scalability under diverse clinical settings. Comparative experiments against bicubic interpolation, conventional supervised U-Net baselines, and alternative diffusion priors demonstrate that our method consistently yields more precise anatomical structures, improved delineation of corneal layers, and superior noise suppression. Quantitative results show state-of-the-art performance in peak signal-to-noise ratio, structural similarity index, and perceptual metrics. This work highlights the potential of diffusion-driven plug-and-play reconstruction to deliver high-fidelity, high-resolution OCT imaging, supporting more reliable clinical assessments and enabling advanced image-guided interventions. Our findings suggest the approach can be extended to other biomedical imaging modalities requiring robust super-resolution and denoising.

Physics-based generation of multilayer corneal OCT data via Gaussian modeling and MCML for AI-driven diagnostic and surgical guidance applications

Training deep learning models for corneal optical coherence tomography (OCT) imaging is limited by the availability of large, well-annotated datasets. We present a configurable Monte Carlo simulation framework that generates synthetic corneal B-scan optical OCT images with pixel-level five-layer segmentation labels derived directly from the simulation geometry. A five-layer corneal model with Gaussian surfaces captures curvature and thickness variability in healthy and keratoconic eyes. Each layer is assigned optical properties from the literature and light transport is simulated using Monte Carlo modeling of light transport in multi-layered tissues (MCML), while incorporating system features such as the confocal PSF and sensitivity roll-off. This approach produces over 10,000 high-resolution (1024x1024) image-label pairs and supports customization of geometry, photon count, noise, and system parameters. The resulting dataset enables systematic training, validation, and benchmarking of AI models under controlled, ground-truth conditions, providing a reproducible and scalable resource to support the development of diagnostic and surgical guidance applications in image-guided ophthalmology.

Real-time topology-aware M-mode OCT segmentation for robotic deep anterior lamellar keratoplasty (DALK) guidance

Robotic deep anterior lamellar keratoplasty (DALK) requires accurate real time depth feedback to approach Descemet's membrane (DM) without perforation. M-mode intraoperative optical coherence tomography (OCT) provides high temporal resolution depth traces, but speckle noise, attenuation, and instrument induced shadowing often result in discontinuous or ambiguous layer interfaces that challenge anatomically consistent segmentation at deployment frame rates. We present a lightweight, topology aware M-mode segmentation pipeline based on UNeXt that incorporates anatomical topology regularization to stabilize boundary continuity and layer ordering under low signal to noise ratio conditions. The proposed system achieves end to end throughput exceeding 80 Hz measured over the complete preprocessing inference overlay pipeline on a single GPU, demonstrating practical real time guidance beyond model only timing. This operating margin provides temporal headroom to reject low quality or dropout frames while maintaining a stable effective depth update rate. Evaluation on a standard rabbit eye M-mode dataset using an established baseline protocol shows improved qualitative boundary stability compared with topology agnostic controls, while preserving deployable real time performance.

Wide-field high-resolution microscopy via high-speed galvo scanning and real-time mosaicking

Wide-field high-resolution microscopy requires fast scanning and accurate image mosaicking to cover large fields of view without compromising image quality. However, conventional galvanometric scanning, particularly under sinusoidal driving, can introduce nonuniform spatial sampling, leading to geometric inconsistencies and brightness variations across the scanned field. To address these challenges, we present an image mosaicking framework for wide-field microscopic imaging that is applicable to both linear and sinusoidal galvanometric scanning strategies. The proposed approach combines a translation-based geometric mosaicking model with region-of-interest (ROI) based brightness correction and seam-aware feathering to improve radiometric consistency across large fields of view. The method relies on calibrated scan parameters and synchronized scan--camera control, without requiring image-content-based registration. Using the proposed framework, wide-field mosaicked images were successfully reconstructed under both linear and sinusoidal scanning strategies, achieving a field of view of up to $2.5 \times 2.5~\mathrm{cm}^2$ with a total acquisition time of approximately $6~\mathrm{s}$ per dataset. Quantitative evaluation shows that both scanning strategies demonstrate improved image quality, including enhanced brightness uniformity, increased contrast-to-noise ratio (CNR), and reduced seam-related artifacts after image processing, while preserving a lateral resolution of $7.81~μ\mathrm{m}$. Overall, the presented framework provides a practical and efficient solution for scan-based wide-field microscopic mosaicking.

Bias in, Bias out: Annotation Bias in Multilingual Large Language Models

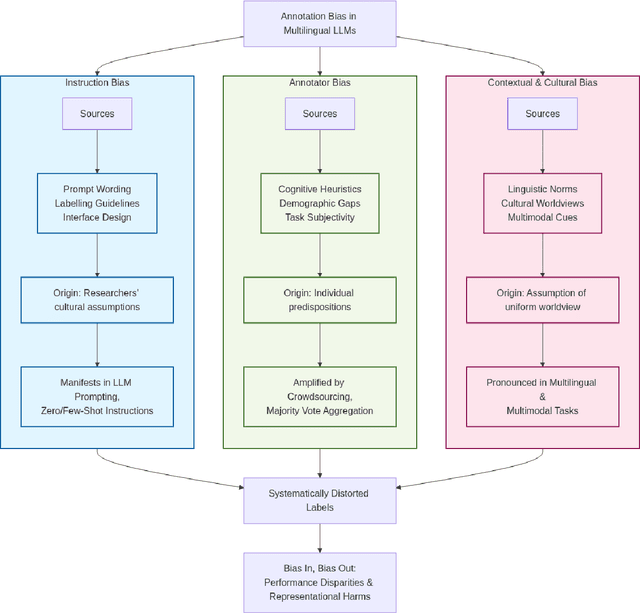
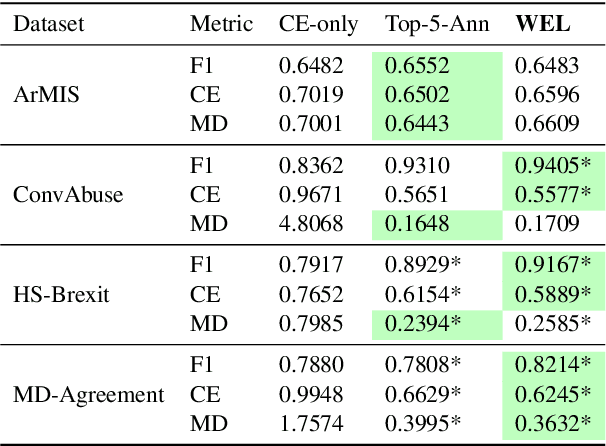
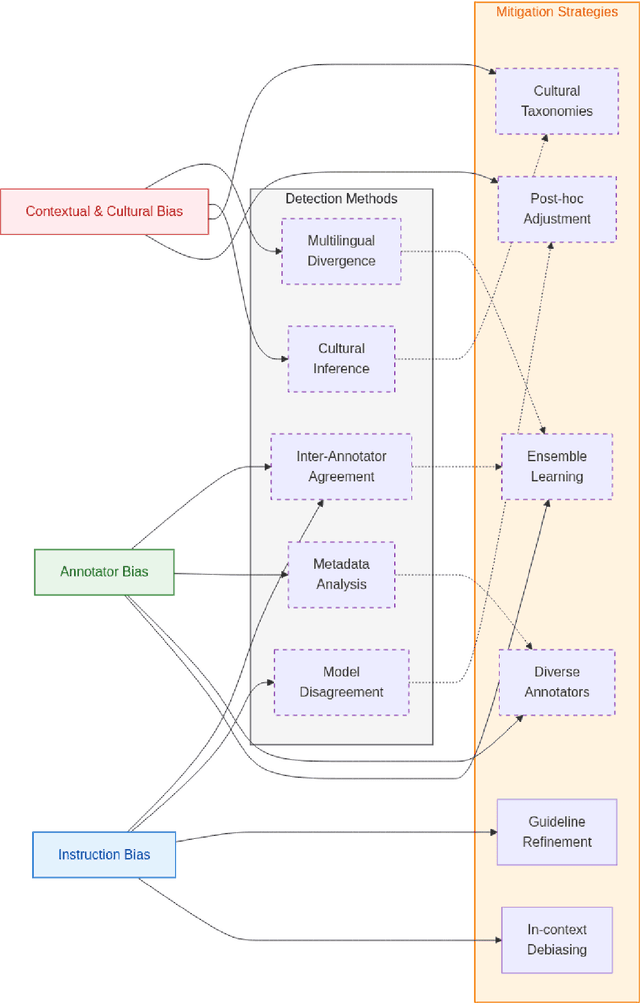
Annotation bias in NLP datasets remains a major challenge for developing multilingual Large Language Models (LLMs), particularly in culturally diverse settings. Bias from task framing, annotator subjectivity, and cultural mismatches can distort model outputs and exacerbate social harms. We propose a comprehensive framework for understanding annotation bias, distinguishing among instruction bias, annotator bias, and contextual and cultural bias. We review detection methods (including inter-annotator agreement, model disagreement, and metadata analysis) and highlight emerging techniques such as multilingual model divergence and cultural inference. We further outline proactive and reactive mitigation strategies, including diverse annotator recruitment, iterative guideline refinement, and post-hoc model adjustments. Our contributions include: (1) a typology of annotation bias; (2) a synthesis of detection metrics; (3) an ensemble-based bias mitigation approach adapted for multilingual settings, and (4) an ethical analysis of annotation processes. Together, these insights aim to inform more equitable and culturally grounded annotation pipelines for LLMs.

Interpretable Credit Default Prediction with Ensemble Learning and SHAP

This study focuses on the problem of credit default prediction, builds a modeling framework based on machine learning, and conducts comparative experiments on a variety of mainstream classification algorithms. Through preprocessing, feature engineering, and model training of the Home Credit dataset, the performance of multiple models including logistic regression, random forest, XGBoost, LightGBM, etc. in terms of accuracy, precision, and recall is evaluated. The results show that the ensemble learning method has obvious advantages in predictive performance, especially in dealing with complex nonlinear relationships between features and data imbalance problems. It shows strong robustness. At the same time, the SHAP method is used to analyze the importance and dependency of features, and it is found that the external credit score variable plays a dominant role in model decision making, which helps to improve the model's interpretability and practical application value. The research results provide effective reference and technical support for the intelligent development of credit risk control systems.

Post-interactive Multimodal Trajectory Prediction for Autonomous Driving

Modeling the interactions among agents for trajectory prediction of autonomous driving has been challenging due to the inherent uncertainty in agents' behavior. The interactions involved in the predicted trajectories of agents, also called post-interactions, have rarely been considered in trajectory prediction models. To this end, we propose a coarse-to-fine Transformer for multimodal trajectory prediction, i.e., Pioformer, which explicitly extracts the post-interaction features to enhance the prediction accuracy. Specifically, we first build a Coarse Trajectory Network to generate coarse trajectories based on the observed trajectories and lane segments, in which the low-order interaction features are extracted with the graph neural networks. Next, we build a hypergraph neural network-based Trajectory Proposal Network to generate trajectory proposals, where the high-order interaction features are learned by the hypergraphs. Finally, the trajectory proposals are sent to the Proposal Refinement Network for further refinement. The observed trajectories and trajectory proposals are concatenated together as the inputs of the Proposal Refinement Network, in which the post-interaction features are learned by combining the previous interaction features and trajectory consistency features. Moreover, we propose a three-stage training scheme to facilitate the learning process. Extensive experiments on the Argoverse 1 dataset demonstrate the superiority of our method. Compared with the baseline HiVT-64, our model has reduced the prediction errors by 4.4%, 8.4%, 14.4%, 5.7% regarding metrics minADE6, minFDE6, MR6, and brier-minFDE6, respectively.

Knowledge-Decoupled Synergetic Learning: An MLLM based Collaborative Approach to Few-shot Multimodal Dialogue Intention Recognition

Few-shot multimodal dialogue intention recognition is a critical challenge in the e-commerce domainn. Previous methods have primarily enhanced model classification capabilities through post-training techniques. However, our analysis reveals that training for few-shot multimodal dialogue intention recognition involves two interconnected tasks, leading to a seesaw effect in multi-task learning. This phenomenon is attributed to knowledge interference stemming from the superposition of weight matrix updates during the training process. To address these challenges, we propose Knowledge-Decoupled Synergetic Learning (KDSL), which mitigates these issues by utilizing smaller models to transform knowledge into interpretable rules, while applying the post-training of larger models. By facilitating collaboration between the large and small multimodal large language models for prediction, our approach demonstrates significant improvements. Notably, we achieve outstanding results on two real Taobao datasets, with enhancements of 6.37\% and 6.28\% in online weighted F1 scores compared to the state-of-the-art method, thereby validating the efficacy of our framework.