Upper Confidence Primal-Dual Optimization: Stochastically Constrained Markov Decision Processes with Adversarial Losses and Unknown Transitions

We consider online learning for episodic Markov decision processes (MDPs) with stochastic long-term budget constraints, which plays a central role in ensuring the safety of reinforcement learning. Here the loss function can vary arbitrarily across the episodes, whereas both the loss received and the budget consumption are revealed at the end of each episode. Previous works solve this problem under the restrictive assumption that the transition model of the MDP is known a priori and establish regret bounds that depend polynomially on the cardinalities of the state space $\mathcal{S}$ and the action space $\mathcal{A}$. In this work, we propose a new \emph{upper confidence primal-dual} algorithm, which only requires the trajectories sampled from the transition model. In particular, we prove that the proposed algorithm achieves $\tilde{\mathcal{O}}(L|\mathcal{S}|\sqrt{|\mathcal{A}|T})$ upper bounds of both the regret and the constraint violation, where $L$ is the length of each episode. Our analysis incorporates a new high-probability drift analysis of Lagrange multiplier processes into the celebrated regret analysis of upper confidence reinforcement learning, which demonstrates the power of "optimism in the face of uncertainty" in constrained online learning.

Provably Efficient Safe Exploration via Primal-Dual Policy Optimization

We study the Safe Reinforcement Learning (SRL) problem using the Constrained Markov Decision Process (CMDP) formulation in which an agent aims to maximize the expected total reward subject to a safety constraint on the expected total value of a criterion function (e.g., utility). We focus on an episodic setting with the function approximation where the reward and criterion functions and the Markov transition kernels all have a linear structure but do not impose any additional assumptions on the sampling model. Designing SRL algorithms with provable computational and statistical efficiency is particularly challenging under this setting because of the need to incorporate both the safety constraint and the function approximation into the fundamental exploitation/exploration tradeoff. To this end, we present an {O}ptimistic {P}rimal-{D}ual Proximal Policy {OP}timization (OPDOP) algorithm where the value function is estimated by combining the least-squares policy evaluation and an additional bonus term for safe exploration. We prove that the proposed algorithm achieves an O(d^{1.5}H^{3.5}\sqrt{T}) regret and an O(d^{1.5}H^{3.5}\sqrt{T}) constraint violation, where d is the dimension of the feature mapping, H is the horizon of each episode, and T is the total number of steps. We establish these bounds under the following two settings: (i) Both the reward and criterion functions can change adversarially but are revealed entirely after each episode. (ii) The reward/criterion functions are fixed but the feedback after each episode is bandit. Our bounds depend on the capacity of the state space only through the dimension of the feature mapping and thus our results hold even when the number of states goes to infinity. To the best of our knowledge, we provide the first provably efficient policy optimization algorithm for CMDPs with safe exploration.

Pontryagin Differentiable Programming: An End-to-End Learning and Control Framework

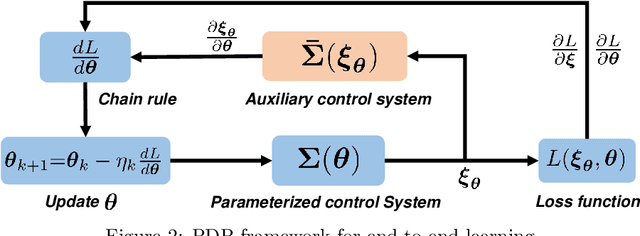
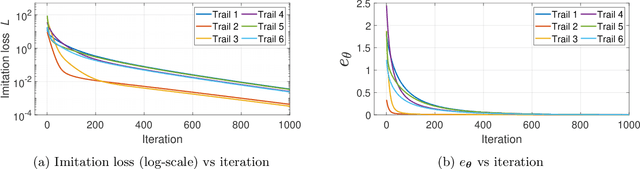
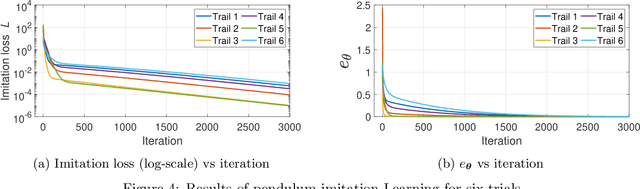
This paper develops a Pontryagin differentiable programming (PDP) methodology to establish a unified end-to-end learning framework, which solves a large class of learning and control tasks. The proposed PDP framework distinguishes itself from existing ones by two key techniques: first, by differentiating the Pontryagin's Maximum Principle, the PDP framework allows end-to-end learning of a large class of parameterized systems, even when differentiation with respect to an unknown objective function is not readily attainable; and second, based on control theory, the PDP framework incorporates both the forward and backward propagations by constructing two control systems, respectively, which are then efficiently solved using techniques in control domain. Three learning modes of the proposed PDP framework are investigated to address three types of learning problems: inverse optimization, system identification, and control/planning, respectively. Effectiveness of the PDP framework in each learning mode has been validated in the context of pendulum systems.

On Computation and Generalization of Generative Adversarial Imitation Learning

Generative Adversarial Imitation Learning (GAIL) is a powerful and practical approach for learning sequential decision-making policies. Different from Reinforcement Learning (RL), GAIL takes advantage of demonstration data by experts (e.g., human), and learns both the policy and reward function of the unknown environment. Despite the significant empirical progresses, the theory behind GAIL is still largely unknown. The major difficulty comes from the underlying temporal dependency of the demonstration data and the minimax computational formulation of GAIL without convex-concave structure. To bridge such a gap between theory and practice, this paper investigates the theoretical properties of GAIL. Specifically, we show: (1) For GAIL with general reward parameterization, the generalization can be guaranteed as long as the class of the reward functions is properly controlled; (2) For GAIL, where the reward is parameterized as a reproducing kernel function, GAIL can be efficiently solved by stochastic first order optimization algorithms, which attain sublinear convergence to a stationary solution. To the best of our knowledge, these are the first results on statistical and computational guarantees of imitation learning with reward/policy function approximation. Numerical experiments are provided to support our analysis.

Natural Actor-Critic Converges Globally for Hierarchical Linear Quadratic Regulator

Multi-agent reinforcement learning has been successfully applied to a number of challenging problems. Despite these empirical successes, theoretical understanding of different algorithms is lacking, primarily due to the curse of dimensionality caused by the exponential growth of the state-action space with the number of agents. We study a fundamental problem of multi-agent linear quadratic regulator in a setting where the agents are partially exchangeable. In this setting, we develop a hierarchical actor-critic algorithm, whose computational complexity is independent of the total number of agents, and prove its global linear convergence to the optimal policy. As linear quadratic regulators are often used to approximate general dynamic systems, this paper provided an important step towards better understanding of general hierarchical mean-field multi-agent reinforcement learning.

Provably Efficient Exploration in Policy Optimization

While policy-based reinforcement learning (RL) achieves tremendous successes in practice, it is significantly less understood in theory, especially compared with value-based RL. In particular, it remains elusive how to design a provably efficient policy optimization algorithm that incorporates exploration. To bridge such a gap, this paper proposes an Optimistic variant of the Proximal Policy Optimization algorithm (OPPO), which follows an "optimistic version" of the policy gradient direction. This paper proves that, in the problem of episodic Markov decision process with linear function approximation, unknown transition, and adversarial reward with full-information feedback, OPPO achieves $\tilde{O}(\sqrt{d^3 H^3 T})$ regret. Here $d$ is the feature dimension, $H$ is the episode horizon, and $T$ is the total number of steps. To the best of our knowledge, OPPO is the first provably efficient policy optimization algorithm that explores.

Decentralized Multi-Agent Reinforcement Learning with Networked Agents: Recent Advances

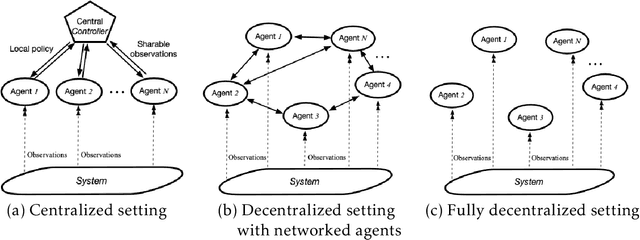
Multi-agent reinforcement learning (MARL) has long been a significant and everlasting research topic in both machine learning and control. With the recent development of (single-agent) deep RL, there is a resurgence of interests in developing new MARL algorithms, especially those that are backed by theoretical analysis. In this paper, we review some recent advances a sub-area of this topic: decentralized MARL with networked agents. Specifically, multiple agents perform sequential decision-making in a common environment, without the coordination of any central controller. Instead, the agents are allowed to exchange information with their neighbors over a communication network. Such a setting finds broad applications in the control and operation of robots, unmanned vehicles, mobile sensor networks, and smart grid. This review is built upon several our research endeavors in this direction, together with some progresses made by other researchers along the line. We hope this review to inspire the devotion of more research efforts to this exciting yet challenging area.

Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms

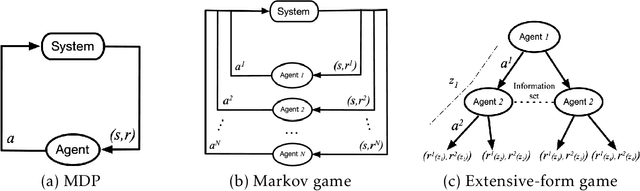
Recent years have witnessed significant advances in reinforcement learning (RL), which has registered great success in solving various sequential decision-making problems in machine learning. Most of the successful RL applications, e.g., the games of Go and Poker, robotics, and autonomous driving, involve the participation of more than one single agent, which naturally fall into the realm of multi-agent RL (MARL), a domain with a relatively long history, and has recently re-emerged due to advances in single-agent RL techniques. Though empirically successful, theoretical foundations for MARL are relatively lacking in the literature. In this chapter, we provide a selective overview of MARL, with focus on algorithms backed by theoretical analysis. More specifically, we review the theoretical results of MARL algorithms mainly within two representative frameworks, Markov/stochastic games and extensive-form games, in accordance with the types of tasks they address, i.e., fully cooperative, fully competitive, and a mix of the two. We also introduce several significant but challenging applications of these algorithms. Orthogonal to the existing reviews on MARL, we highlight several new angles and taxonomies of MARL theory, including learning in extensive-form games, decentralized MARL with networked agents, MARL in the mean-field regime, (non-)convergence of policy-based methods for learning in games, etc. Some of the new angles extrapolate from our own research endeavors and interests. Our overall goal with this chapter is, beyond providing an assessment of the current state of the field on the mark, to identify fruitful future research directions on theoretical studies of MARL. We expect this chapter to serve as continuing stimulus for researchers interested in working on this exciting while challenging topic.

Convergent Policy Optimization for Safe Reinforcement Learning

We study the safe reinforcement learning problem with nonlinear function approximation, where policy optimization is formulated as a constrained optimization problem with both the objective and the constraint being nonconvex functions. For such a problem, we construct a sequence of surrogate convex constrained optimization problems by replacing the nonconvex functions locally with convex quadratic functions obtained from policy gradient estimators. We prove that the solutions to these surrogate problems converge to a stationary point of the original nonconvex problem. Furthermore, to extend our theoretical results, we apply our algorithm to examples of optimal control and multi-agent reinforcement learning with safety constraints.

Actor-Critic Provably Finds Nash Equilibria of Linear-Quadratic Mean-Field Games

We study discrete-time mean-field Markov games with infinite numbers of agents where each agent aims to minimize its ergodic cost. We consider the setting where the agents have identical linear state transitions and quadratic cost functions, while the aggregated effect of the agents is captured by the population mean of their states, namely, the mean-field state. For such a game, based on the Nash certainty equivalence principle, we provide sufficient conditions for the existence and uniqueness of its Nash equilibrium. Moreover, to find the Nash equilibrium, we propose a mean-field actor-critic algorithm with linear function approximation, which does not require knowing the model of dynamics. Specifically, at each iteration of our algorithm, we use the single-agent actor-critic algorithm to approximately obtain the optimal policy of the each agent given the current mean-field state, and then update the mean-field state. In particular, we prove that our algorithm converges to the Nash equilibrium at a linear rate. To the best of our knowledge, this is the first success of applying model-free reinforcement learning with function approximation to discrete-time mean-field Markov games with provable non-asymptotic global convergence guarantees.