Yuwei Luo
Can We Validate Counterfactual Estimations in the Presence of General Network Interference?
Feb 03, 2025



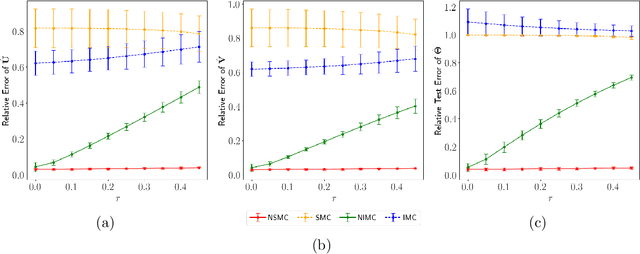
Abstract:In experimental settings with network interference, a unit's treatment can influence outcomes of other units, challenging both causal effect estimation and its validation. Classic validation approaches fail as outcomes are only observable under one treatment scenario and exhibit complex correlation patterns due to interference. To address these challenges, we introduce a new framework enabling cross-validation for counterfactual estimation. At its core is our distribution-preserving network bootstrap method -- a theoretically-grounded approach inspired by approximate message passing. This method creates multiple subpopulations while preserving the underlying distribution of network effects. We extend recent causal message-passing developments by incorporating heterogeneous unit-level characteristics and varying local interactions, ensuring reliable finite-sample performance through non-asymptotic analysis. We also develop and publicly release a comprehensive benchmark toolbox with diverse experimental environments, from networks of interacting AI agents to opinion formation in real-world communities and ride-sharing applications. These environments provide known ground truth values while maintaining realistic complexities, enabling systematic examination of causal inference methods. Extensive evaluation across these environments demonstrates our method's robustness to diverse forms of network interference. Our work provides researchers with both a practical estimation framework and a standardized platform for testing future methodological developments.
Higher-Order Causal Message Passing for Experimentation with Complex Interference
Nov 01, 2024



Abstract:Accurate estimation of treatment effects is essential for decision-making across various scientific fields. This task, however, becomes challenging in areas like social sciences and online marketplaces, where treating one experimental unit can influence outcomes for others through direct or indirect interactions. Such interference can lead to biased treatment effect estimates, particularly when the structure of these interactions is unknown. We address this challenge by introducing a new class of estimators based on causal message-passing, specifically designed for settings with pervasive, unknown interference. Our estimator draws on information from the sample mean and variance of unit outcomes and treatments over time, enabling efficient use of observed data to estimate the evolution of the system state. Concretely, we construct non-linear features from the moments of unit outcomes and treatments and then learn a function that maps these features to future mean and variance of unit outcomes. This allows for the estimation of the treatment effect over time. Extensive simulations across multiple domains, using synthetic and real network data, demonstrate the efficacy of our approach in estimating total treatment effect dynamics, even in cases where interference exhibits non-monotonic behavior in the probability of treatment.
Geometry-Aware Approaches for Balancing Performance and Theoretical Guarantees in Linear Bandits
Jun 26, 2023



Abstract:This paper is motivated by recent developments in the linear bandit literature, which have revealed a discrepancy between the promising empirical performance of algorithms such as Thompson sampling and Greedy, when compared to their pessimistic theoretical regret bounds. The challenge arises from the fact that while these algorithms may perform poorly in certain problem instances, they generally excel in typical instances. To address this, we propose a new data-driven technique that tracks the geometry of the uncertainty ellipsoid, enabling us to establish an instance-dependent frequentist regret bound for a broad class of algorithms, including Greedy, OFUL, and Thompson sampling. This result empowers us to identify and ``course-correct" instances in which the base algorithms perform poorly. The course-corrected algorithms achieve the minimax optimal regret of order $\tilde{\mathcal{O}}(d\sqrt{T})$, while retaining most of the desirable properties of the base algorithms. We present simulation results to validate our findings and compare the performance of our algorithms with the baselines.
Dynamic Regret Minimization for Control of Non-stationary Linear Dynamical Systems
Nov 06, 2021
Abstract:We consider the problem of controlling a Linear Quadratic Regulator (LQR) system over a finite horizon $T$ with fixed and known cost matrices $Q,R$, but unknown and non-stationary dynamics $\{A_t, B_t\}$. The sequence of dynamics matrices can be arbitrary, but with a total variation, $V_T$, assumed to be $o(T)$ and unknown to the controller. Under the assumption that a sequence of stabilizing, but potentially sub-optimal controllers is available for all $t$, we present an algorithm that achieves the optimal dynamic regret of $\tilde{\mathcal{O}}\left(V_T^{2/5}T^{3/5}\right)$. With piece-wise constant dynamics, our algorithm achieves the optimal regret of $\tilde{\mathcal{O}}(\sqrt{ST})$ where $S$ is the number of switches. The crux of our algorithm is an adaptive non-stationarity detection strategy, which builds on an approach recently developed for contextual Multi-armed Bandit problems. We also argue that non-adaptive forgetting (e.g., restarting or using sliding window learning with a static window size) may not be regret optimal for the LQR problem, even when the window size is optimally tuned with the knowledge of $V_T$. The main technical challenge in the analysis of our algorithm is to prove that the ordinary least squares (OLS) estimator has a small bias when the parameter to be estimated is non-stationary. Our analysis also highlights that the key motif driving the regret is that the LQR problem is in spirit a bandit problem with linear feedback and locally quadratic cost. This motif is more universal than the LQR problem itself, and therefore we believe our results should find wider application.
Semiparametric Nonlinear Bipartite Graph Representation Learning with Provable Guarantees
Mar 02, 2020

Abstract:Graph representation learning is a ubiquitous task in machine learning where the goal is to embed each vertex into a low-dimensional vector space. We consider the bipartite graph and formalize its representation learning problem as a statistical estimation problem of parameters in a semiparametric exponential family distribution. The bipartite graph is assumed to be generated by a semiparametric exponential family distribution, whose parametric component is given by the proximity of outputs of two one-layer neural networks, while nonparametric (nuisance) component is the base measure. Neural networks take high-dimensional features as inputs and output embedding vectors. In this setting, the representation learning problem is equivalent to recovering the weight matrices. The main challenges of estimation arise from the nonlinearity of activation functions and the nonparametric nuisance component of the distribution. To overcome these challenges, we propose a pseudo-likelihood objective based on the rank-order decomposition technique and focus on its local geometry. We show that the proposed objective is strongly convex in a neighborhood around the ground truth, so that a gradient descent-based method achieves linear convergence rate. Moreover, we prove that the sample complexity of the problem is linear in dimensions (up to logarithmic factors), which is consistent with parametric Gaussian models. However, our estimator is robust to any model misspecification within the exponential family, which is validated in extensive experiments.
Natural Actor-Critic Converges Globally for Hierarchical Linear Quadratic Regulator
Dec 14, 2019

Abstract:Multi-agent reinforcement learning has been successfully applied to a number of challenging problems. Despite these empirical successes, theoretical understanding of different algorithms is lacking, primarily due to the curse of dimensionality caused by the exponential growth of the state-action space with the number of agents. We study a fundamental problem of multi-agent linear quadratic regulator in a setting where the agents are partially exchangeable. In this setting, we develop a hierarchical actor-critic algorithm, whose computational complexity is independent of the total number of agents, and prove its global linear convergence to the optimal policy. As linear quadratic regulators are often used to approximate general dynamic systems, this paper provided an important step towards better understanding of general hierarchical mean-field multi-agent reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge