Variational Integrators and Graph-Based Solvers for Multibody Dynamics in Maximal Coordinates

Multibody dynamics simulators are an important tool in many fields, including learning and control for robotics. However, many existing dynamics simulators suffer from inaccuracies when dealing with constrained mechanical systems due to unsuitable integrators and dissatisfying constraint handling. Variational integrators are numerical discretization methods that can reduce physical inaccuracies when simulating mechanical systems, and formulating the dynamics in maximal coordinates allows for easy and numerically robust incorporation of constraints such as kinematic loops or contacts. Therefore, this article derives a variational integrator for mechanical systems with equality and inequality constraints in maximal coordinates. Additionally, efficient graph-based sparsity-exploiting algorithms for solving the integrator are provided and implemented as an open-source simulator. The evaluation of the simulator shows the improved physical accuracy due to the variational integrator and the advantages of the sparse solvers, while application examples of a walking robot and an exoskeleton with explicit constraints demonstrate the necessity and capabilities of maximal coordinates.

Aquarium: A Fully Differentiable Fluid-Structure Interaction Solver for Robotics Applications

We present Aquarium, a differentiable fluid-structure interaction solver for robotics that offers stable simulation, accurate coupled robot-fluid physics, and full differentiability with respect to fluid states, robot states, and shape parameters. Aquarium achieves stable simulation with accurate flow physics by integrating over the discrete, incompressible Navier-Stokes equations directly using a fully-implicit Crank-Nicolson scheme with a second-order finite-volume spatial discretization. The robot and fluid physics are coupled using the immersed boundary method by formulating the no-slip condition as an equality constraint applied directly to the Navier-Stokes system. This choice of coupling allows the fluid-structure interaction to be posed and solved as a nonlinear optimization problem. This optimization-based formulation is then exploited using the implicit-function theorem to compute derivatives. The derivatives can then be passed to a gradient-based optimization or learning framework. We demonstrate Aquarium's ability to accurately simulate coupled fluid-solid physics with numerous examples, including a cylinder in free stream and a soft robotic tail with hardware validation. We also demonstrate Aquarium's ability to provide full, analytical gradients by performing both shape and gait optimization of a robotic fish tail to maximize generated thrust.

Single-Level Differentiable Contact Simulation

We present a differentiable formulation of rigid-body contact dynamics for objects and robots represented as compositions of convex primitives. Existing optimization-based approaches simulating contact between convex primitives rely on a bilevel formulation that separates collision detection and contact simulation. These approaches are unreliable in realistic contact simulation scenarios because isolating the collision detection problem introduces contact location non-uniqueness. Our approach combines contact simulation and collision detection into a unified single-level optimization problem. This disambiguates the collision detection problem in a physics-informed manner. Compared to previous differentiable simulation approaches, our formulation features improved simulation robustness and a reduction in computational complexity by more than an order of magnitude. We illustrate the contact and collision differentiability on a robotic manipulation task requiring optimization-through-contact. We provide a numerically efficient implementation of our formulation in the Julia language called Silico.jl.

Differentiable Physics Simulation of Dynamics-Augmented Neural Objects

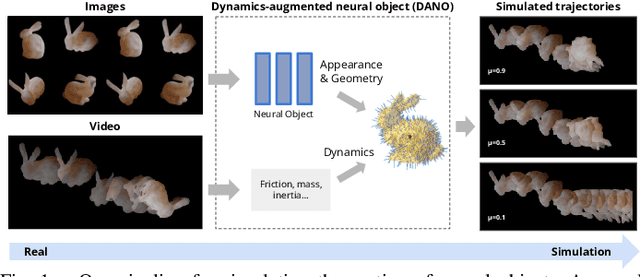
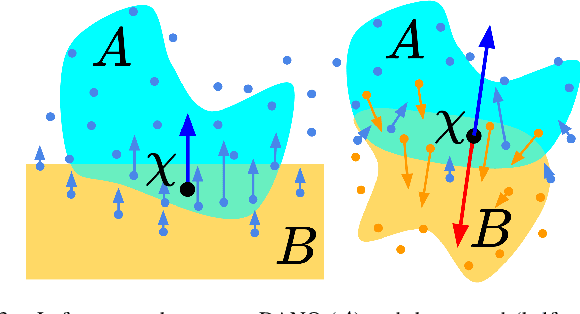
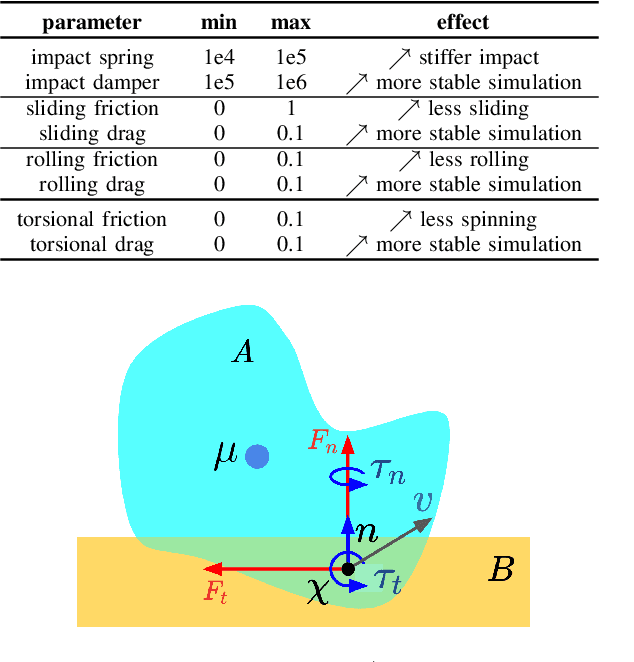
We present a differentiable pipeline for simulating the motion of objects that represent their geometry as a continuous density field parameterized as a deep network. This includes Neural Radiance Fields (NeRFs), and other related models. From the density field, we estimate the dynamical properties of the object, including its mass, center of mass, and inertia matrix. We then introduce a differentiable contact model based on the density field for computing normal and friction forces resulting from collisions. This allows a robot to autonomously build object models that are visually and dynamically accurate from still images and videos of objects in motion. The resulting Dynamics-Augmented Neural Objects (DANOs) are simulated with an existing differentiable simulation engine, Dojo, interacting with other standard simulation objects, such as spheres, planes, and robots specified as URDFs. A robot can use this simulation to optimize grasps and manipulation trajectories of neural objects, or to improve the neural object models through gradient-based real-to-simulation transfer. We demonstrate the pipeline to learn the coefficient of friction of a bar of soap from a real video of the soap sliding on a table. We also learn the coefficient of friction and mass of a Stanford bunny through interactions with a Panda robot arm from synthetic data, and we optimize trajectories in simulation for the Panda arm to push the bunny to a goal location.

Cerberus: Low-Drift Visual-Inertial-Leg Odometry For Agile Locomotion

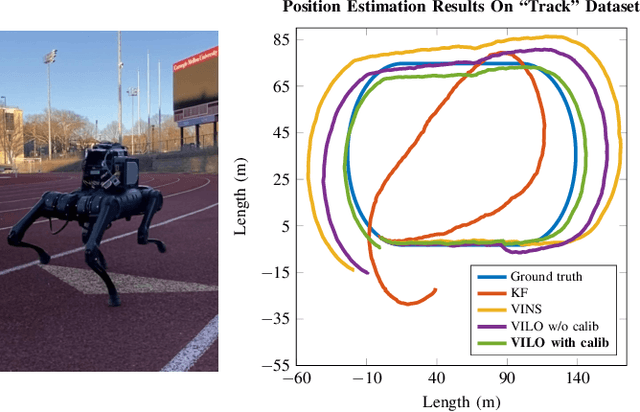
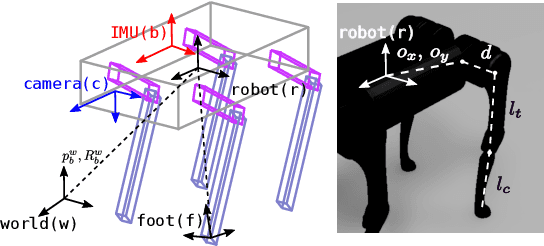
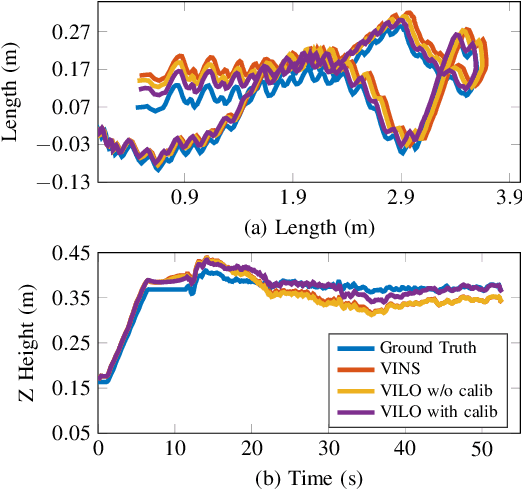
We present an open-source Visual-Inertial-Leg Odometry (VILO) state estimation solution, Cerberus, for legged robots that estimates position precisely on various terrains in real time using a set of standard sensors, including stereo cameras, IMU, joint encoders, and contact sensors. In addition to estimating robot states, we also perform online kinematic parameter calibration and contact outlier rejection to substantially reduce position drift. Hardware experiments in various indoor and outdoor environments validate that calibrating kinematic parameters within the Cerberus can reduce estimation drift to lower than 1% during long distance high speed locomotion. Our drift results are better than any other state estimation method using the same set of sensors reported in the literature. Moreover, our state estimator performs well even when the robot is experiencing large impacts and camera occlusion. The implementation of the state estimator, along with the datasets used to compute our results, are available at https://github.com/ShuoYangRobotics/Cerberus.

Differentiable Collision Detection for a Set of Convex Primitives

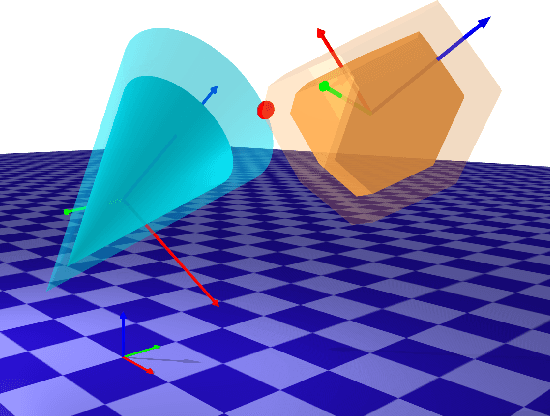
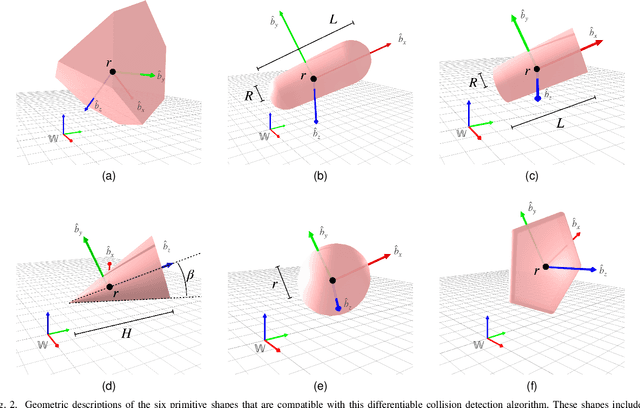
Collision detection between objects is critical for simulation, control, and learning for robotic systems. However, existing collision detection routines are inherently non-differentiable, limiting their usefulness in optimization-based algorithms. In this work, we propose a fully differentiable collision-detection framework that reasons about distances between a set of composable and highly expressive convex primitive shapes. This is achieved by formulating the collision detection problem as a convex optimization problem that seeks to find the minimum uniform scaling to be applied to each object before there is an intersection. The optimization problem is fully differentiable and is able to return both the collision detection status as well as the contact points on each object.

DiffPills: Differentiable Collision Detection for Capsules and Padded Polygons

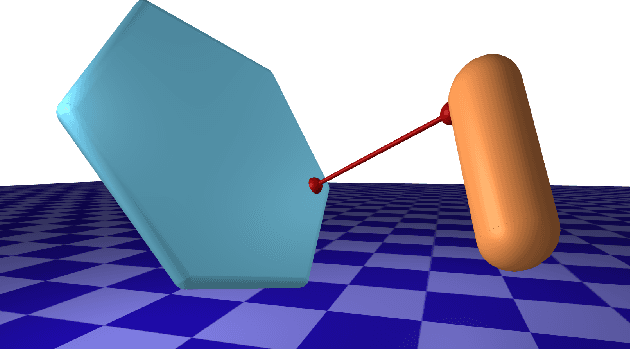
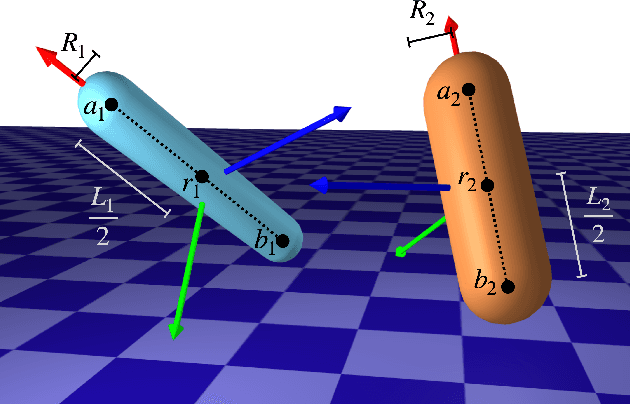
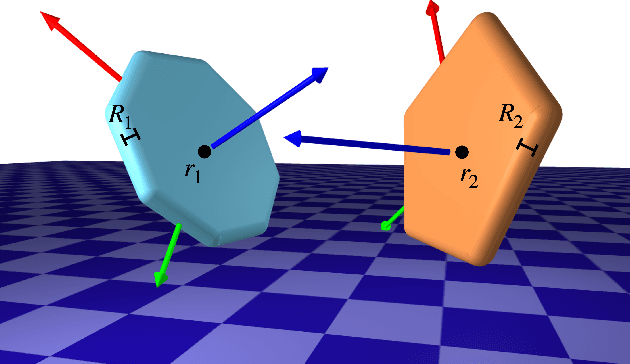
Collision detection plays an important role in simulation, control, and learning for robotic systems. However, no existing method is differentiable with respect to the configurations of the objects, greatly limiting the sort of algorithms that can be built on top of collision detection. In this work, we propose a set of differentiable collision detection algorithms between capsules and padded polygons by formulating these problems as differentiable convex quadratic programs. The resulting algorithms are able to return a proximity value indicating if a collision has taken place, as well as the closest points between objects, all of which are differentiable. As a result, they can be used reliably within other gradient-based optimization methods, including trajectory optimization, state estimation, and reinforcement learning methods.

Low-latency Imaging and Inference from LoRa-enabled CubeSats

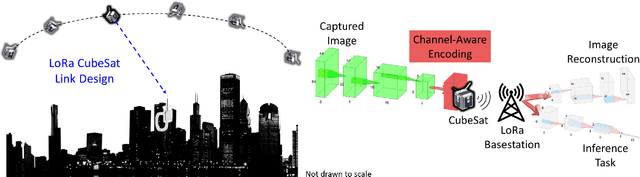
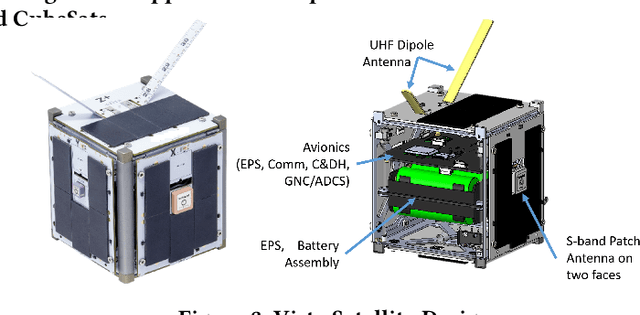
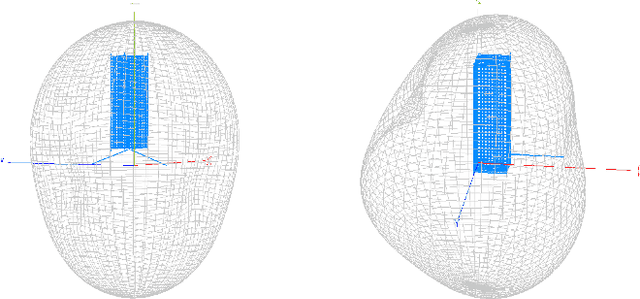
Recent years have seen the rapid deployment of low-cost CubeSats in low-Earth orbit, primarily for research, education, and Earth observation. The vast majority of these CubeSats experience significant latency (several hours) from the time an image is captured to the time it is available on the ground. This is primarily due to the limited availability of dedicated satellite ground stations that tend to be bulky to deploy and expensive to rent. This paper explores using LoRa radios in the ISM band for low-latency downlink communication from CubeSats, primarily due to the availability of extensive ground LoRa infrastructure and minimal interference to terrestrial communication. However, the limited bandwidth of LoRa precludes rich satellite Earth images to be sent - instead, the CubeSats can at best send short messages (a few hundred bytes). This paper details our experience in communicating with a LoRa-enabled CubeSat launched by our team. We present Vista, a communication system that makes software modifications to LoRa encoding onboard a CubeSat and decoding on commercial LoRa ground stations to allow for satellite imagery to be communicated, as well as wide-ranging machine learning inference on these images. This is achieved through a LoRa-channel-aware image encoding that is informed by the structure of satellite images, the tasks performed on it, as well as the Doppler variation of satellite signals. A detailed evaluation of Vista through trace-driven emulation with traces from the LoRa-CubeSat launch (in 2021) shows 4.56 dB improvement in LoRa image PSNR and 1.38x improvement in land-use classification over those images.

CALIPSO: A Differentiable Solver for Trajectory Optimization with Conic and Complementarity Constraints

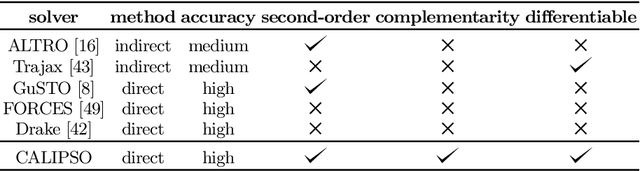
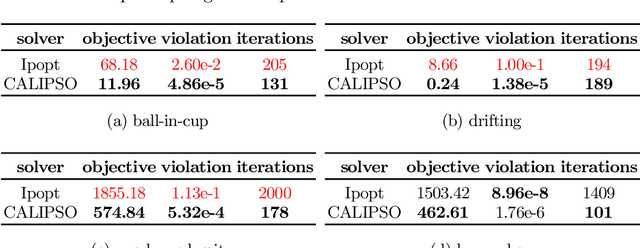
We present a new solver for non-convex trajectory optimization problems that is specialized for robotics applications. CALIPSO, or the Conic Augmented Lagrangian Interior-Point SOlver, combines several strategies for constrained numerical optimization to natively handle second-order cones and complementarity constraints. It reliably solves challenging motion-planning problems that include contact-implicit formulations of impacts and Coulomb friction, thrust limits subject to conic constraints, and state-triggered constraints where general-purpose nonlinear programming solvers like SNOPT and Ipopt fail to converge. Additionally, CALIPSO supports efficient differentiation of solutions with respect to problem data, enabling bi-level optimization applications like auto-tuning of feedback policies. Reliable convergence of the solver is demonstrated on a range of problems from manipulation, locomotion, and aerospace domains. An open-source implementation of this solver is available.

Dojo: A Differentiable Simulator for Robotics

We present a differentiable rigid-body-dynamics simulator for robotics that prioritizes physical accuracy and differentiability: Dojo. The simulator utilizes an expressive maximal-coordinates representation, achieves stable simulation at low sample rates, and conserves energy and momentum by employing a variational integrator. A nonlinear complementarity problem, with nonlinear friction cones, models hard contact and is reliably solved using a custom primal-dual interior-point method. The implicit-function theorem enables efficient differentiation of an intermediate relaxed problem and computes smooth gradients from the contact model. We demonstrate the usefulness of the simulator and its gradients through a number of examples including: simulation, trajectory optimization, reinforcement learning, and system identification.