Why Quantization Improves Generalization: NTK of Binary Weight Neural Networks

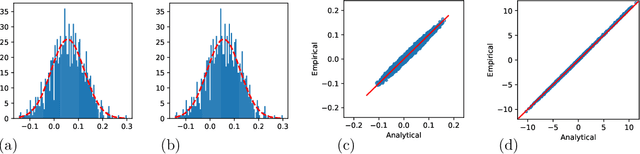
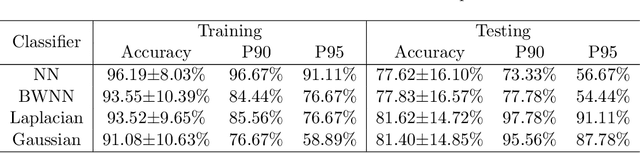
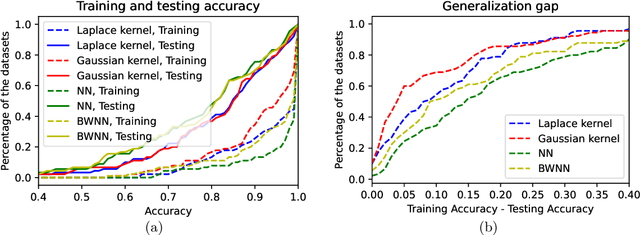
Quantized neural networks have drawn a lot of attention as they reduce the space and computational complexity during the inference. Moreover, there has been folklore that quantization acts as an implicit regularizer and thus can improve the generalizability of neural networks, yet no existing work formalizes this interesting folklore. In this paper, we take the binary weights in a neural network as random variables under stochastic rounding, and study the distribution propagation over different layers in the neural network. We propose a quasi neural network to approximate the distribution propagation, which is a neural network with continuous parameters and smooth activation function. We derive the neural tangent kernel (NTK) for this quasi neural network, and show that the eigenvalue of NTK decays at approximately exponential rate, which is comparable to that of Gaussian kernel with randomized scale. This in turn indicates that the Reproducing Kernel Hilbert Space (RKHS) of a binary weight neural network covers a strict subset of functions compared with the one with real value weights. We use experiments to verify that the quasi neural network we proposed can well approximate binary weight neural network. Furthermore, binary weight neural network gives a lower generalization gap compared with real value weight neural network, which is similar to the difference between Gaussian kernel and Laplace kernel.

Offline Stochastic Shortest Path: Learning, Evaluation and Towards Optimality

Goal-oriented Reinforcement Learning, where the agent needs to reach the goal state while simultaneously minimizing the cost, has received significant attention in real-world applications. Its theoretical formulation, stochastic shortest path (SSP), has been intensively researched in the online setting. Nevertheless, it remains understudied when such an online interaction is prohibited and only historical data is provided. In this paper, we consider the offline stochastic shortest path problem when the state space and the action space are finite. We design the simple value iteration-based algorithms for tackling both offline policy evaluation (OPE) and offline policy learning tasks. Notably, our analysis of these simple algorithms yields strong instance-dependent bounds which can imply worst-case bounds that are near-minimax optimal. We hope our study could help illuminate the fundamental statistical limits of the offline SSP problem and motivate further studies beyond the scope of current consideration.

Offline Reinforcement Learning with Differential Privacy

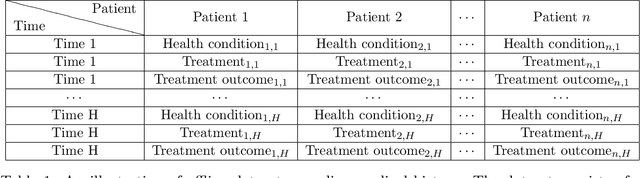
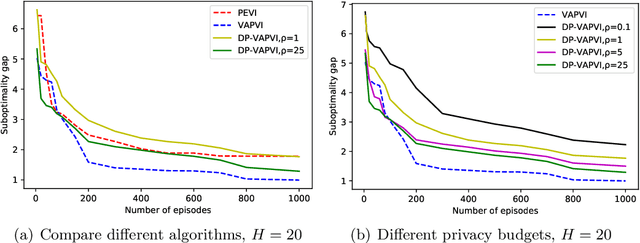
The offline reinforcement learning (RL) problem is often motivated by the need to learn data-driven decision policies in financial, legal and healthcare applications. However, the learned policy could retain sensitive information of individuals in the training data (e.g., treatment and outcome of patients), thus susceptible to various privacy risks. We design offline RL algorithms with differential privacy guarantees which provably prevent such risks. These algorithms also enjoy strong instance-dependent learning bounds under both tabular and linear Markov decision process (MDP) settings. Our theory and simulation suggest that the privacy guarantee comes at (almost) no drop in utility comparing to the non-private counterpart for a medium-size dataset.

Second Order Path Variationals in Non-Stationary Online Learning

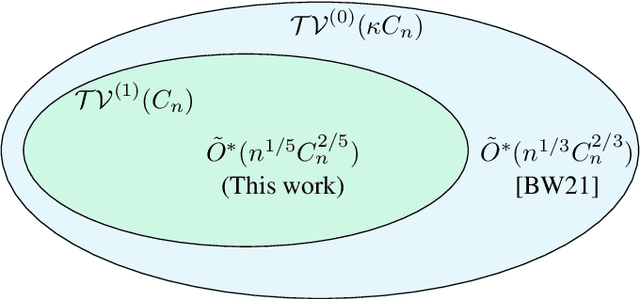
We consider the problem of universal dynamic regret minimization under exp-concave and smooth losses. We show that appropriately designed Strongly Adaptive algorithms achieve a dynamic regret of $\tilde O(d^2 n^{1/5} C_n^{2/5} \vee d^2)$, where $n$ is the time horizon and $C_n$ a path variational based on second order differences of the comparator sequence. Such a path variational naturally encodes comparator sequences that are piecewise linear -- a powerful family that tracks a variety of non-stationarity patterns in practice (Kim et al, 2009). The aforementioned dynamic regret rate is shown to be optimal modulo dimension dependencies and poly-logarithmic factors of $n$. Our proof techniques rely on analysing the KKT conditions of the offline oracle and requires several non-trivial generalizations of the ideas in Baby and Wang, 2021, where the latter work only leads to a slower dynamic regret rate of $\tilde O(d^{2.5}n^{1/3}C_n^{2/3} \vee d^{2.5})$ for the current problem.

Provably Confidential Language Modelling

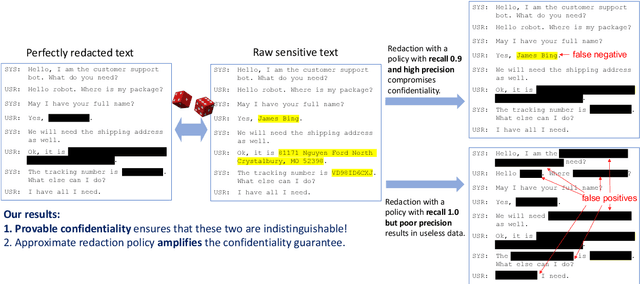
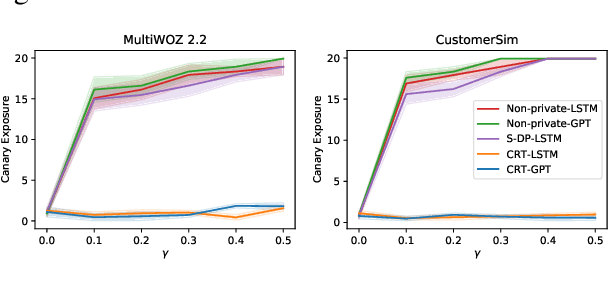
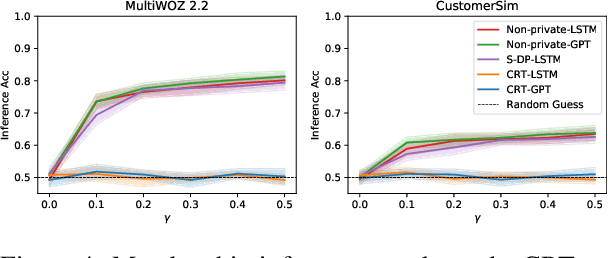
Large language models are shown to memorize privacy information such as social security numbers in training data. Given the sheer scale of the training corpus, it is challenging to screen and filter these privacy data, either manually or automatically. In this paper, we propose Confidentially Redacted Training (CRT), a method to train language generation models while protecting the confidential segments. We borrow ideas from differential privacy (which solves a related but distinct problem) and show that our method is able to provably prevent unintended memorization by randomizing parts of the training process. Moreover, we show that redaction with an approximately correct screening policy amplifies the confidentiality guarantee. We implement the method for both LSTM and GPT language models. Our experimental results show that the models trained by CRT obtain almost the same perplexity while preserving strong confidentiality.

Deep Learning meets Nonparametric Regression: Are Weight-Decayed DNNs Locally Adaptive?

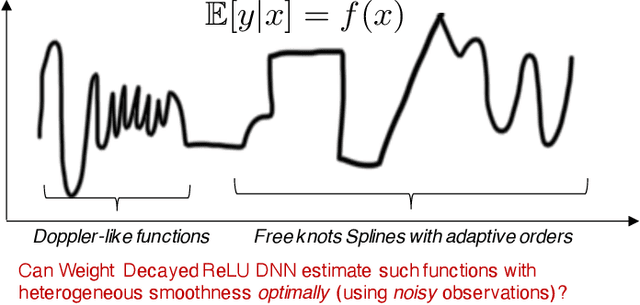
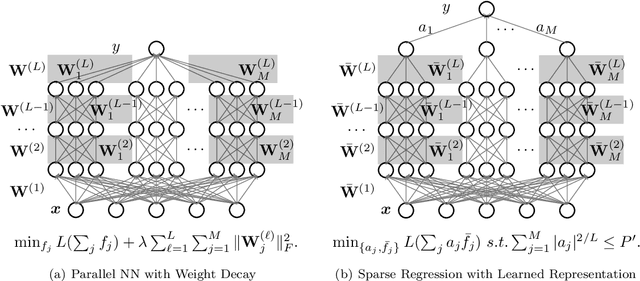
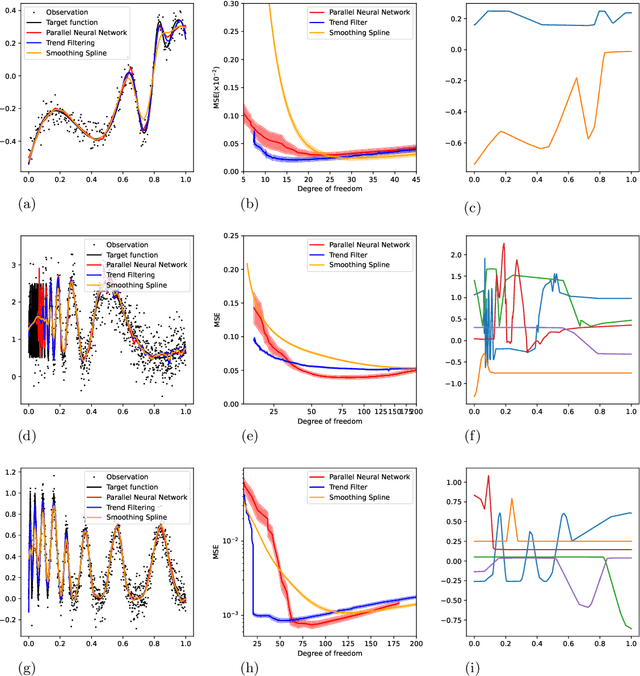
We study the theory of neural network (NN) from the lens of classical nonparametric regression problems with a focus on NN's ability to adaptively estimate functions with heterogeneous smoothness -- a property of functions in Besov or Bounded Variation (BV) classes. Existing work on this problem requires tuning the NN architecture based on the function spaces and sample sizes. We consider a "Parallel NN" variant of deep ReLU networks and show that the standard weight decay is equivalent to promoting the $\ell_p$-sparsity ($0<p<1$) of the coefficient vector of an end-to-end learned function bases, i.e., a dictionary. Using this equivalence, we further establish that by tuning only the weight decay, such Parallel NN achieves an estimation error arbitrarily close to the minimax rates for both the Besov and BV classes. Notably, it gets exponentially closer to minimax optimal as the NN gets deeper. Our research sheds new lights on why depth matters and how NNs are more powerful than kernel methods.

Towards Differential Relational Privacy and its use in Question Answering

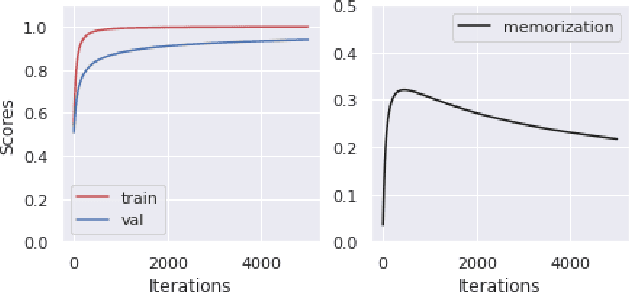
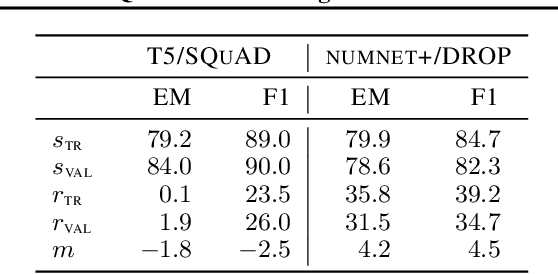
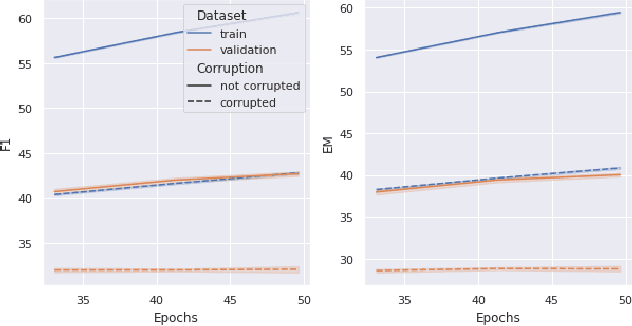
Memorization of the relation between entities in a dataset can lead to privacy issues when using a trained model for question answering. We introduce Relational Memorization (RM) to understand, quantify and control this phenomenon. While bounding general memorization can have detrimental effects on the performance of a trained model, bounding RM does not prevent effective learning. The difference is most pronounced when the data distribution is long-tailed, with many queries having only few training examples: Impeding general memorization prevents effective learning, while impeding only relational memorization still allows learning general properties of the underlying concepts. We formalize the notion of Relational Privacy (RP) and, inspired by Differential Privacy (DP), we provide a possible definition of Differential Relational Privacy (DrP). These notions can be used to describe and compute bounds on the amount of RM in a trained model. We illustrate Relational Privacy concepts in experiments with large-scale models for Question Answering.

Adaptive Private-K-Selection with Adaptive K and Application to Multi-label PATE

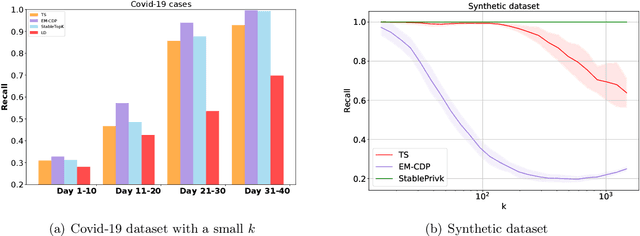
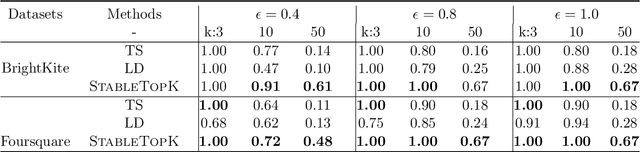
We provide an end-to-end Renyi DP based-framework for differentially private top-$k$ selection. Unlike previous approaches, which require a data-independent choice on $k$, we propose to privately release a data-dependent choice of $k$ such that the gap between $k$-th and the $(k+1)$st "quality" is large. This is achieved by a novel application of the Report-Noisy-Max. Not only does this eliminate one hyperparameter, the adaptive choice of $k$ also certifies the stability of the top-$k$ indices in the unordered set so we can release them using a variant of propose-test-release (PTR) without adding noise. We show that our construction improves the privacy-utility trade-offs compared to the previous top-$k$ selection algorithms theoretically and empirically. Additionally, we apply our algorithm to "Private Aggregation of Teacher Ensembles (PATE)" in multi-label classification tasks with a large number of labels and show that it leads to significant performance gains.

Mixed Differential Privacy in Computer Vision

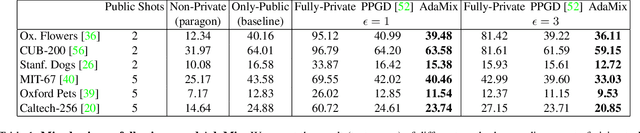
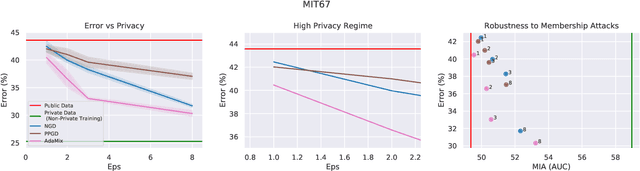
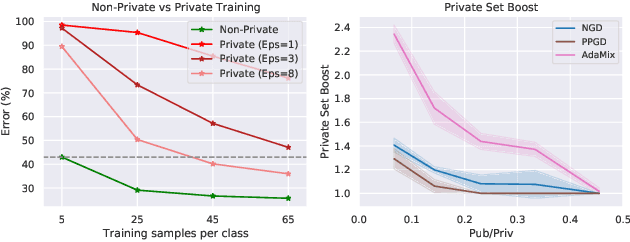
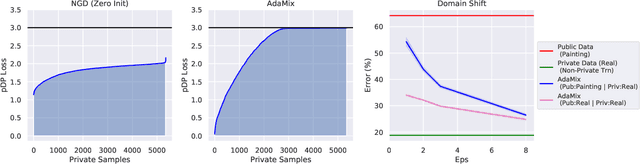
We introduce AdaMix, an adaptive differentially private algorithm for training deep neural network classifiers using both private and public image data. While pre-training language models on large public datasets has enabled strong differential privacy (DP) guarantees with minor loss of accuracy, a similar practice yields punishing trade-offs in vision tasks. A few-shot or even zero-shot learning baseline that ignores private data can outperform fine-tuning on a large private dataset. AdaMix incorporates few-shot training, or cross-modal zero-shot learning, on public data prior to private fine-tuning, to improve the trade-off. AdaMix reduces the error increase from the non-private upper bound from the 167-311\% of the baseline, on average across 6 datasets, to 68-92\% depending on the desired privacy level selected by the user. AdaMix tackles the trade-off arising in visual classification, whereby the most privacy sensitive data, corresponding to isolated points in representation space, are also critical for high classification accuracy. In addition, AdaMix comes with strong theoretical privacy guarantees and convergence analysis.

Near-optimal Offline Reinforcement Learning with Linear Representation: Leveraging Variance Information with Pessimism

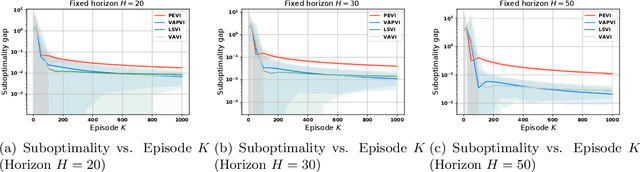
Offline reinforcement learning, which seeks to utilize offline/historical data to optimize sequential decision-making strategies, has gained surging prominence in recent studies. Due to the advantage that appropriate function approximators can help mitigate the sample complexity burden in modern reinforcement learning problems, existing endeavors usually enforce powerful function representation models (e.g. neural networks) to learn the optimal policies. However, a precise understanding of the statistical limits with function representations, remains elusive, even when such a representation is linear. Towards this goal, we study the statistical limits of offline reinforcement learning with linear model representations. To derive the tight offline learning bound, we design the variance-aware pessimistic value iteration (VAPVI), which adopts the conditional variance information of the value function for time-inhomogeneous episodic linear Markov decision processes (MDPs). VAPVI leverages estimated variances of the value functions to reweight the Bellman residuals in the least-square pessimistic value iteration and provides improved offline learning bounds over the best-known existing results (whereas the Bellman residuals are equally weighted by design). More importantly, our learning bounds are expressed in terms of system quantities, which provide natural instance-dependent characterizations that previous results are short of. We hope our results draw a clearer picture of what offline learning should look like when linear representations are provided.