Toward Deeper Understanding of Neural Networks: The Power of Initialization and a Dual View on Expressivity

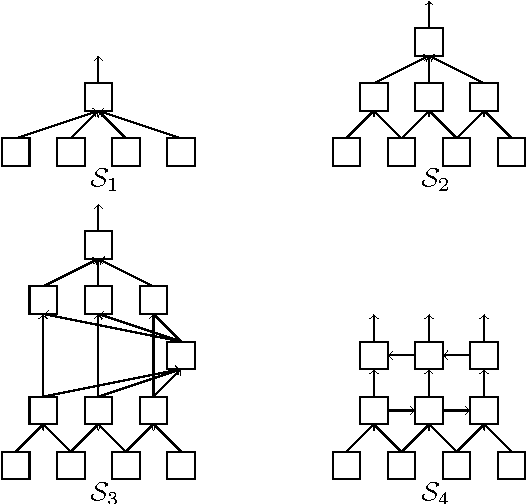
We develop a general duality between neural networks and compositional kernels, striving towards a better understanding of deep learning. We show that initial representations generated by common random initializations are sufficiently rich to express all functions in the dual kernel space. Hence, though the training objective is hard to optimize in the worst case, the initial weights form a good starting point for optimization. Our dual view also reveals a pragmatic and aesthetic perspective of neural networks and underscores their expressive power.

Random Features for Compositional Kernels

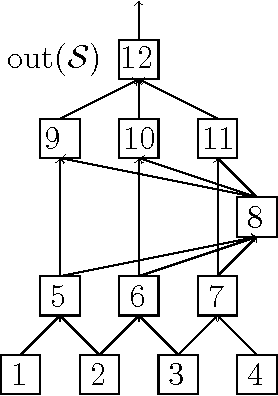
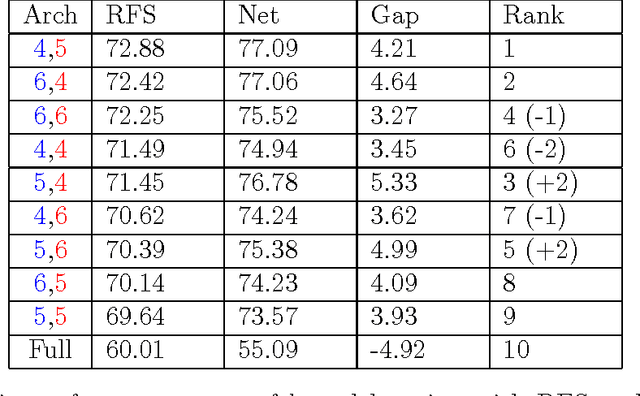
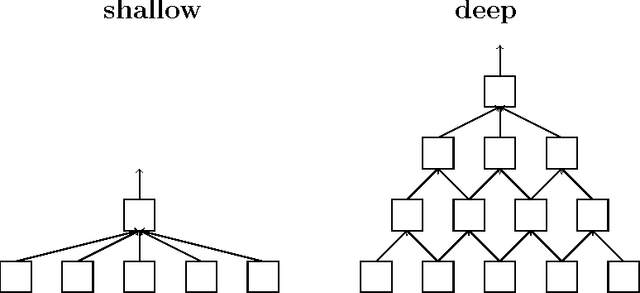
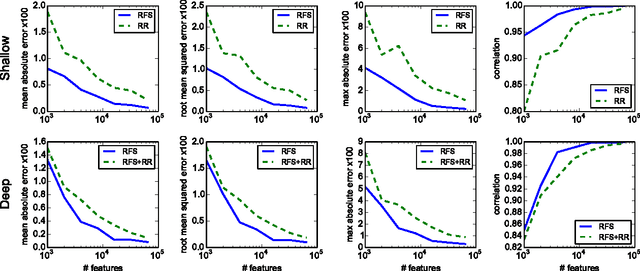
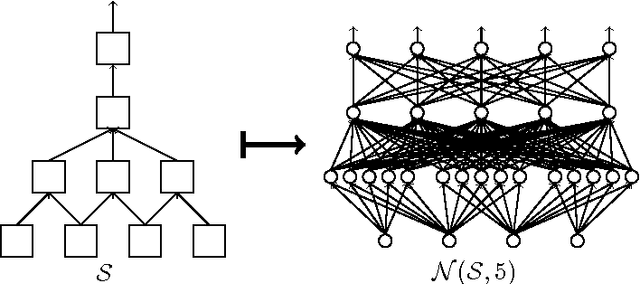
We describe and analyze a simple random feature scheme (RFS) from prescribed compositional kernels. The compositional kernels we use are inspired by the structure of convolutional neural networks and kernels. The resulting scheme yields sparse and efficiently computable features. Each random feature can be represented as an algebraic expression over a small number of (random) paths in a composition tree. Thus, compositional random features can be stored compactly. The discrete nature of the generation process enables de-duplication of repeated features, further compacting the representation and increasing the diversity of the embeddings. Our approach complements and can be combined with previous random feature schemes.

Sketching and Neural Networks

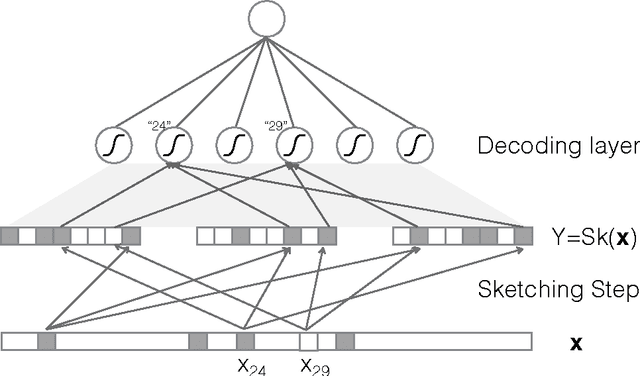
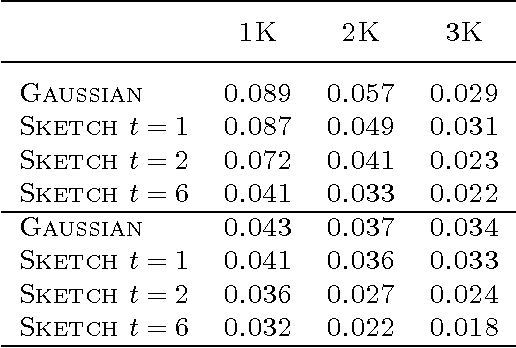
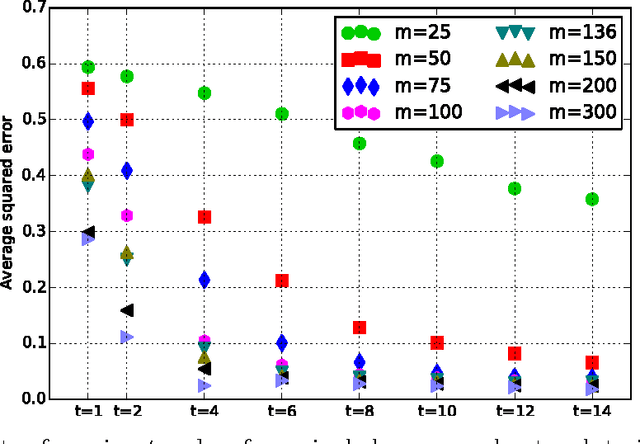
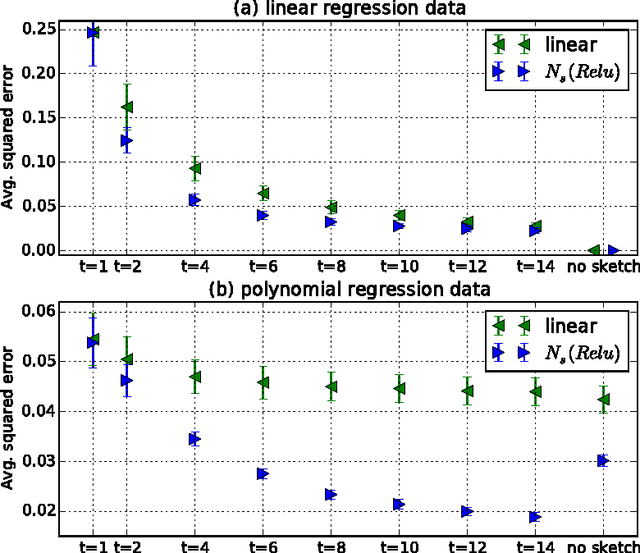
High-dimensional sparse data present computational and statistical challenges for supervised learning. We propose compact linear sketches for reducing the dimensionality of the input, followed by a single layer neural network. We show that any sparse polynomial function can be computed, on nearly all sparse binary vectors, by a single layer neural network that takes a compact sketch of the vector as input. Consequently, when a set of sparse binary vectors is approximately separable using a sparse polynomial, there exists a single-layer neural network that takes a short sketch as input and correctly classifies nearly all the points. Previous work has proposed using sketches to reduce dimensionality while preserving the hypothesis class. However, the sketch size has an exponential dependence on the degree in the case of polynomial classifiers. In stark contrast, our approach of using improper learning, using a larger hypothesis class allows the sketch size to have a logarithmic dependence on the degree. Even in the linear case, our approach allows us to improve on the pesky $O({1}/{{\gamma}^2})$ dependence of random projections, on the margin $\gamma$. We empirically show that our approach leads to more compact neural networks than related methods such as feature hashing at equal or better performance.

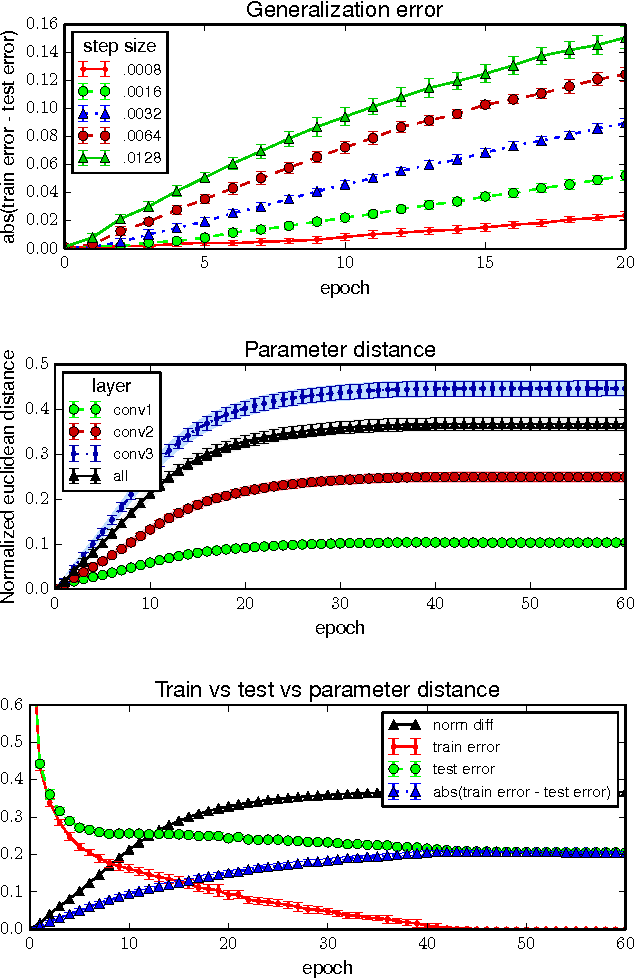
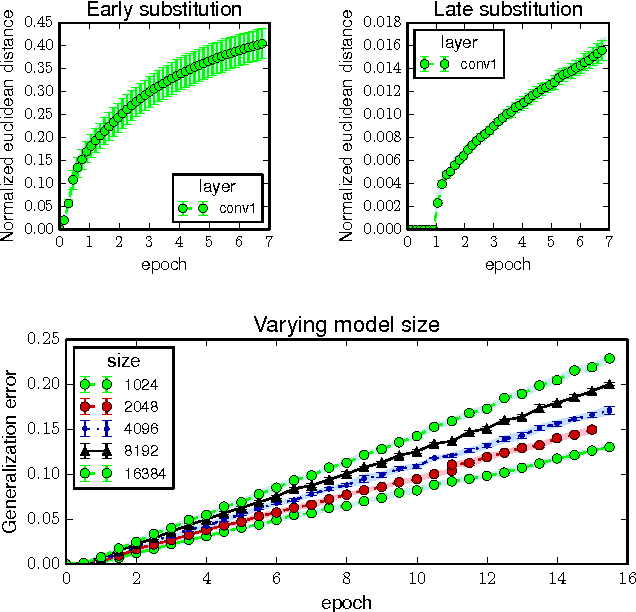
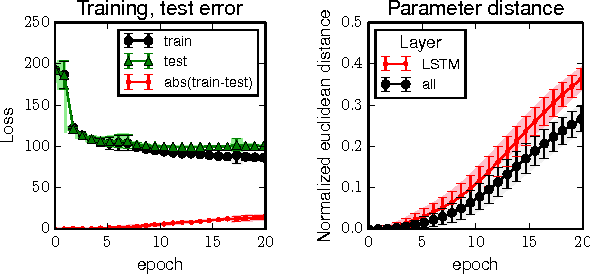
Train faster, generalize better: Stability of stochastic gradient descent

We show that parametric models trained by a stochastic gradient method (SGM) with few iterations have vanishing generalization error. We prove our results by arguing that SGM is algorithmically stable in the sense of Bousquet and Elisseeff. Our analysis only employs elementary tools from convex and continuous optimization. We derive stability bounds for both convex and non-convex optimization under standard Lipschitz and smoothness assumptions. Applying our results to the convex case, we provide new insights for why multiple epochs of stochastic gradient methods generalize well in practice. In the non-convex case, we give a new interpretation of common practices in neural networks, and formally show that popular techniques for training large deep models are indeed stability-promoting. Our findings conceptually underscore the importance of reducing training time beyond its obvious benefit.

Zero-Shot Learning by Convex Combination of Semantic Embeddings

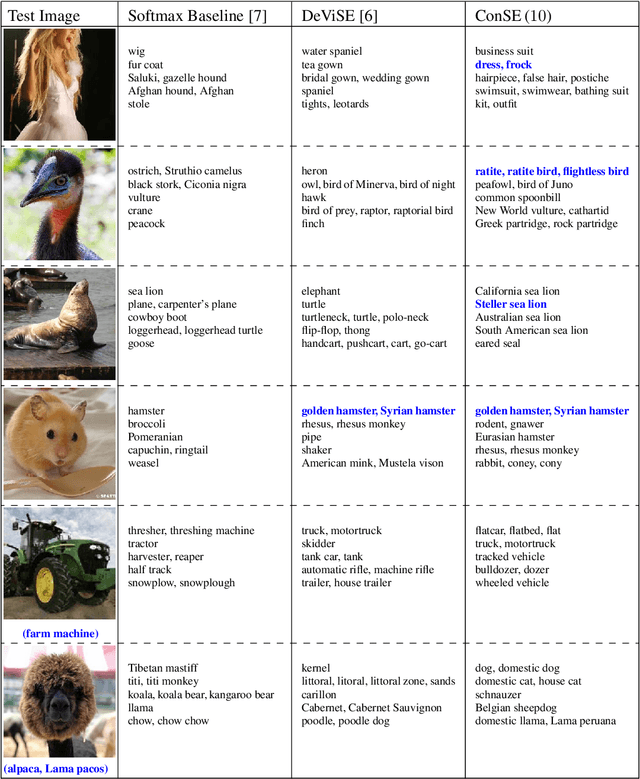
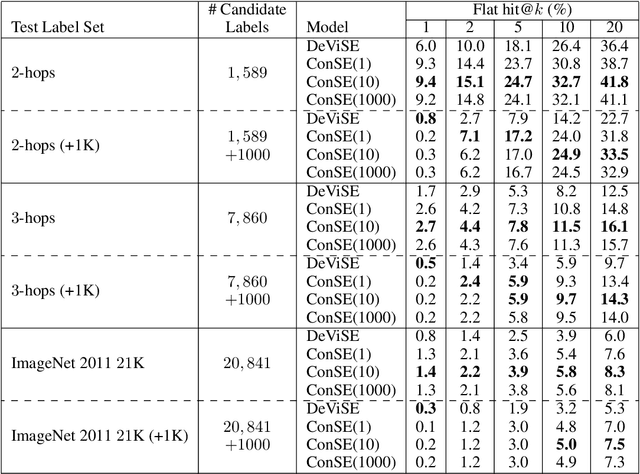
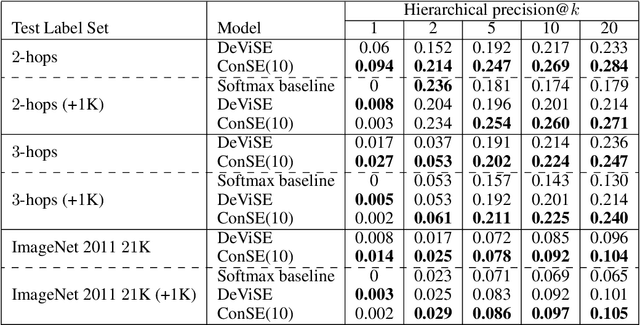
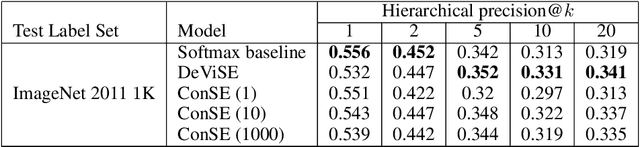
Several recent publications have proposed methods for mapping images into continuous semantic embedding spaces. In some cases the embedding space is trained jointly with the image transformation. In other cases the semantic embedding space is established by an independent natural language processing task, and then the image transformation into that space is learned in a second stage. Proponents of these image embedding systems have stressed their advantages over the traditional \nway{} classification framing of image understanding, particularly in terms of the promise for zero-shot learning -- the ability to correctly annotate images of previously unseen object categories. In this paper, we propose a simple method for constructing an image embedding system from any existing \nway{} image classifier and a semantic word embedding model, which contains the $\n$ class labels in its vocabulary. Our method maps images into the semantic embedding space via convex combination of the class label embedding vectors, and requires no additional training. We show that this simple and direct method confers many of the advantages associated with more complex image embedding schemes, and indeed outperforms state of the art methods on the ImageNet zero-shot learning task.

Using Web Co-occurrence Statistics for Improving Image Categorization

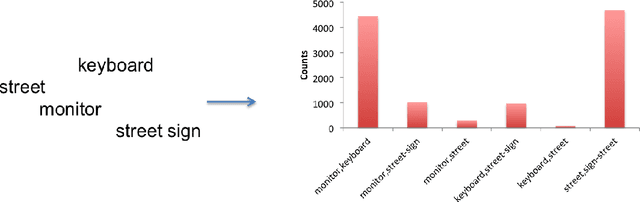
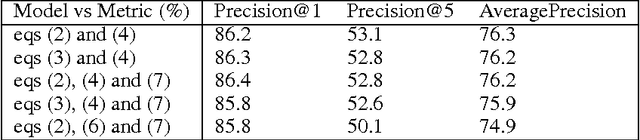
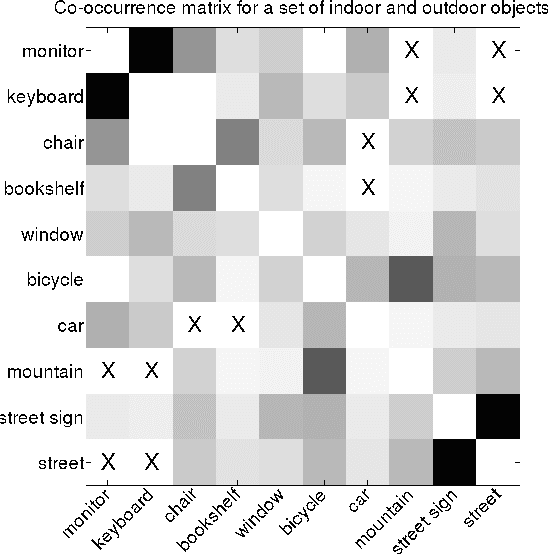
Object recognition and localization are important tasks in computer vision. The focus of this work is the incorporation of contextual information in order to improve object recognition and localization. For instance, it is natural to expect not to see an elephant to appear in the middle of an ocean. We consider a simple approach to encapsulate such common sense knowledge using co-occurrence statistics from web documents. By merely counting the number of times nouns (such as elephants, sharks, oceans, etc.) co-occur in web documents, we obtain a good estimate of expected co-occurrences in visual data. We then cast the problem of combining textual co-occurrence statistics with the predictions of image-based classifiers as an optimization problem. The resulting optimization problem serves as a surrogate for our inference procedure. Albeit the simplicity of the resulting optimization problem, it is effective in improving both recognition and localization accuracy. Concretely, we observe significant improvements in recognition and localization rates for both ImageNet Detection 2012 and Sun 2012 datasets.

The Maximum Entropy Relaxation Path

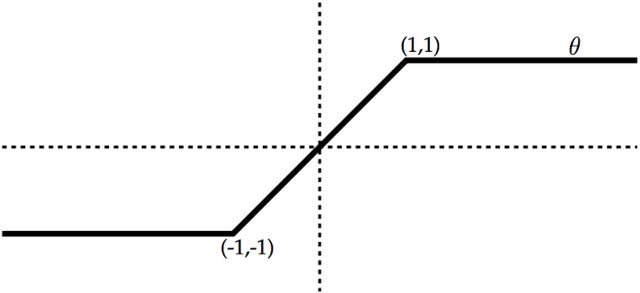
The relaxed maximum entropy problem is concerned with finding a probability distribution on a finite set that minimizes the relative entropy to a given prior distribution, while satisfying relaxed max-norm constraints with respect to a third observed multinomial distribution. We study the entire relaxation path for this problem in detail. We show existence and a geometric description of the relaxation path. Specifically, we show that the maximum entropy relaxation path admits a planar geometric description as an increasing, piecewise linear function in the inverse relaxation parameter. We derive fast algorithms for tracking the path. In various realistic settings, our algorithms require $O(n\log(n))$ operations for probability distributions on $n$ points, making it possible to handle large problems. Once the path has been recovered, we show that given a validation set, the family of admissible models is reduced from an infinite family to a small, discrete set. We demonstrate the merits of our approach in experiments with synthetic data and discuss its potential for the estimation of compact n-gram language models.

Update Rules for Parameter Estimation in Bayesian Networks

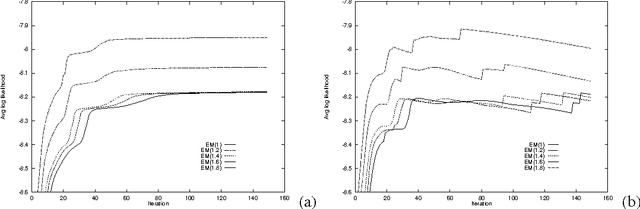
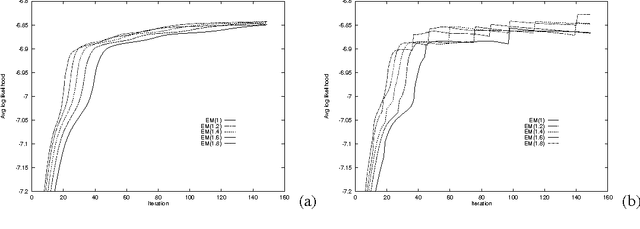
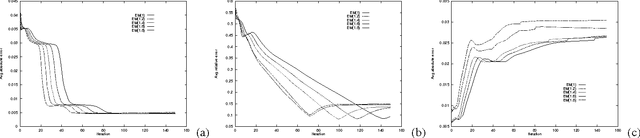
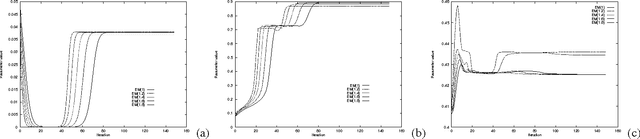
This paper re-examines the problem of parameter estimation in Bayesian networks with missing values and hidden variables from the perspective of recent work in on-line learning [Kivinen & Warmuth, 1994]. We provide a unified framework for parameter estimation that encompasses both on-line learning, where the model is continuously adapted to new data cases as they arrive, and the more traditional batch learning, where a pre-accumulated set of samples is used in a one-time model selection process. In the batch case, our framework encompasses both the gradient projection algorithm and the EM algorithm for Bayesian networks. The framework also leads to new on-line and batch parameter update schemes, including a parameterized version of EM. We provide both empirical and theoretical results indicating that parameterized EM allows faster convergence to the maximum likelihood parameters than does standard EM.

Switching Portfolios

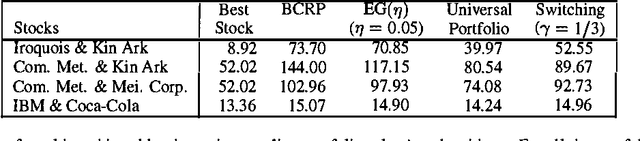
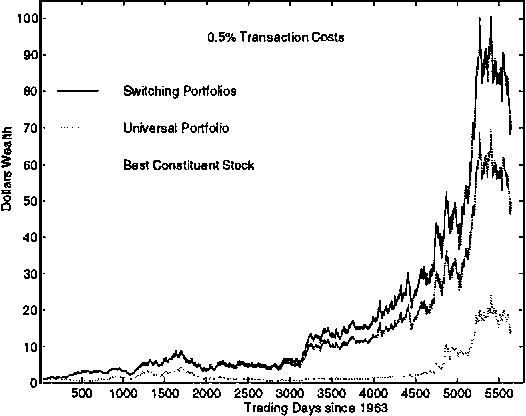
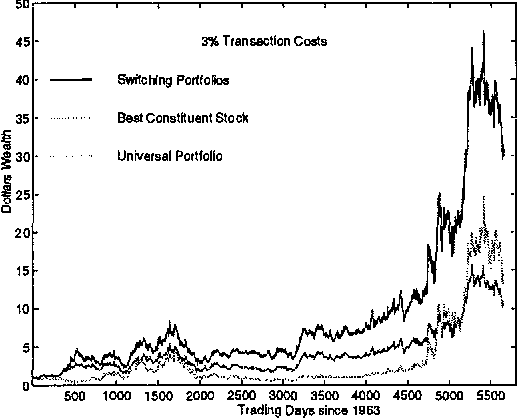
A constant rebalanced portfolio is an asset allocation algorithm which keeps the same distribution of wealth among a set of assets along a period of time. Recently, there has been work on on-line portfolio selection algorithms which are competitive with the best constant rebalanced portfolio determined in hindsight. By their nature, these algorithms employ the assumption that high returns can be achieved using a fixed asset allocation strategy. However, stock markets are far from being stationary and in many cases the wealth achieved by a constant rebalanced portfolio is much smaller than the wealth achieved by an ad-hoc investment strategy that adapts to changes in the market. In this paper we present an efficient Bayesian portfolio selection algorithm that is able to track a changing market. We also describe a simple extension of the algorithm for the case of a general transaction cost, including the transactions cost models recently investigated by Blum and kalai. We provide a simple analysis of the competitiveness of the algorithm and check its performance on real stock data from the New York Stock Exchange accumulated during a 22-year period.

Matrix Approximation under Local Low-Rank Assumption

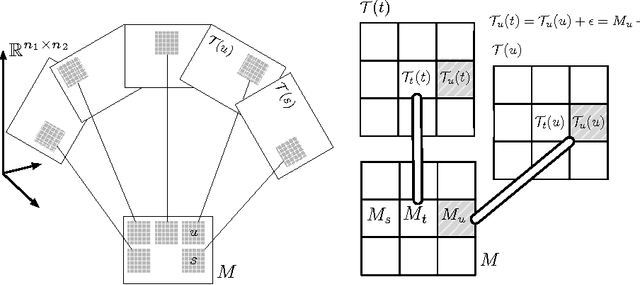
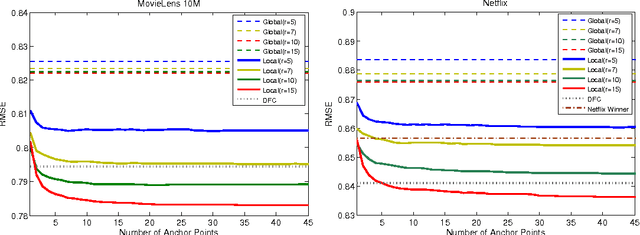
Matrix approximation is a common tool in machine learning for building accurate prediction models for recommendation systems, text mining, and computer vision. A prevalent assumption in constructing matrix approximations is that the partially observed matrix is of low-rank. We propose a new matrix approximation model where we assume instead that the matrix is only locally of low-rank, leading to a representation of the observed matrix as a weighted sum of low-rank matrices. We analyze the accuracy of the proposed local low-rank modeling. Our experiments show improvements in prediction accuracy in recommendation tasks.