C2AL: Cohort-Contrastive Auxiliary Learning for Large-scale Recommendation Systems

Training large-scale recommendation models under a single global objective implicitly assumes homogeneity across user populations. However, real-world data are composites of heterogeneous cohorts with distinct conditional distributions. As models increase in scale and complexity and as more data is used for training, they become dominated by central distribution patterns, neglecting head and tail regions. This imbalance limits the model's learning ability and can result in inactive attention weights or dead neurons. In this paper, we reveal how the attention mechanism can play a key role in factorization machines for shared embedding selection, and propose to address this challenge by analyzing the substructures in the dataset and exposing those with strong distributional contrast through auxiliary learning. Unlike previous research, which heuristically applies weighted labels or multi-task heads to mitigate such biases, we leverage partially conflicting auxiliary labels to regularize the shared representation. This approach customizes the learning process of attention layers to preserve mutual information with minority cohorts while improving global performance. We evaluated C2AL on massive production datasets with billions of data points each for six SOTA models. Experiments show that the factorization machine is able to capture fine-grained user-ad interactions using the proposed method, achieving up to a 0.16% reduction in normalized entropy overall and delivering gains exceeding 0.30% on targeted minority cohorts.

Local Space-Time Smoothing for Version Controlled Documents

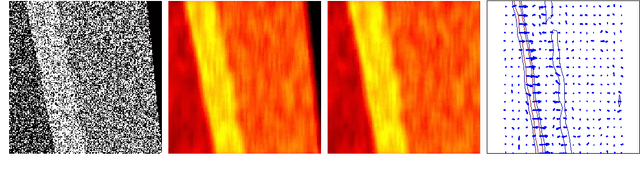
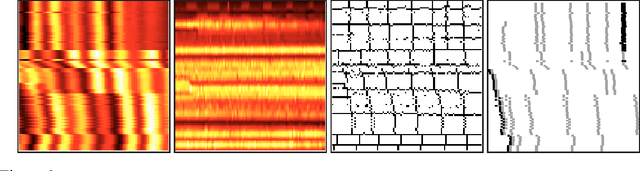
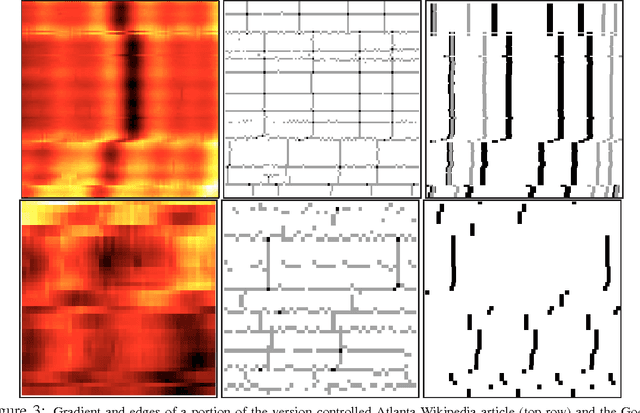
Unlike static documents, version controlled documents are continuously edited by one or more authors. Such collaborative revision process makes traditional modeling and visualization techniques inappropriate. In this paper we propose a new representation based on local space-time smoothing that captures important revision patterns. We demonstrate the applicability of our framework using experiments on synthetic and real-world data.

Beyond Sentiment: The Manifold of Human Emotions

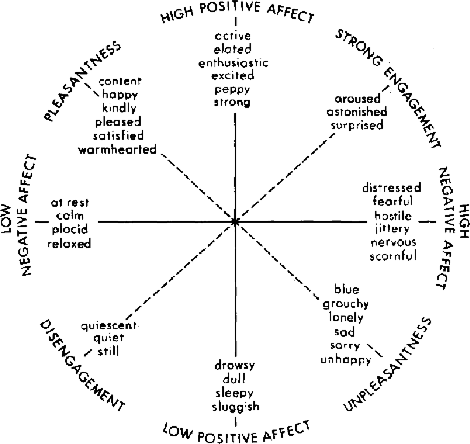
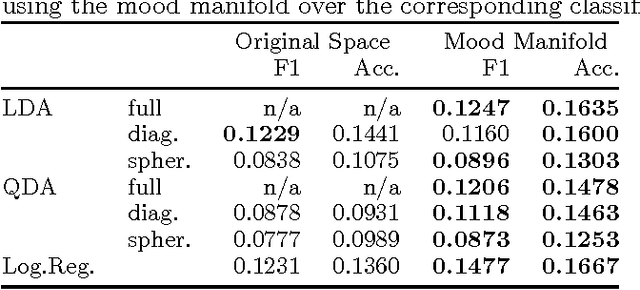
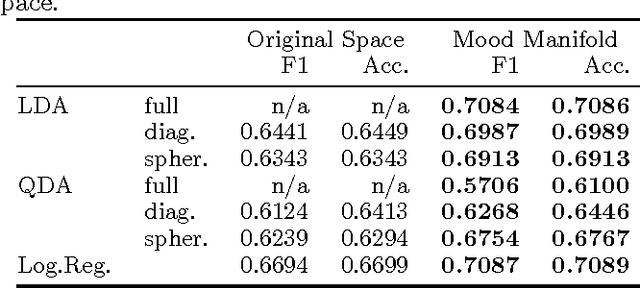
Sentiment analysis predicts the presence of positive or negative emotions in a text document. In this paper we consider higher dimensional extensions of the sentiment concept, which represent a richer set of human emotions. Our approach goes beyond previous work in that our model contains a continuous manifold rather than a finite set of human emotions. We investigate the resulting model, compare it to psychological observations, and explore its predictive capabilities. Besides obtaining significant improvements over a baseline without manifold, we are also able to visualize different notions of positive sentiment in different domains.

A Linear Approximation to the chi^2 Kernel with Geometric Convergence

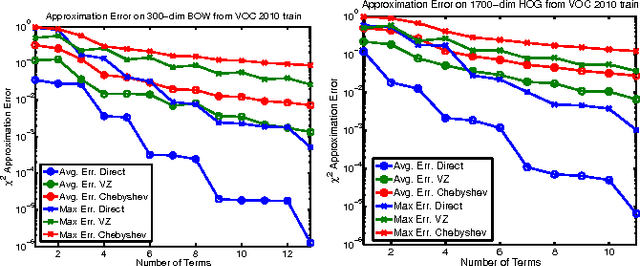
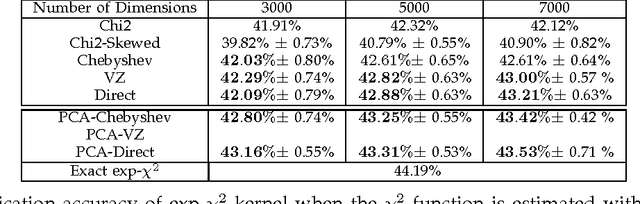
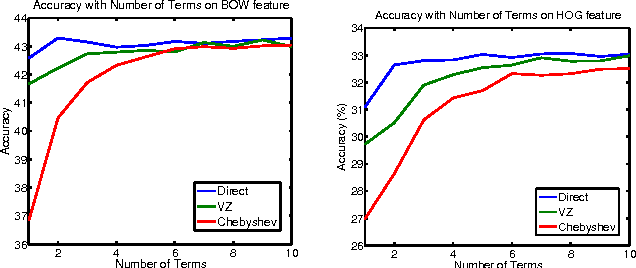
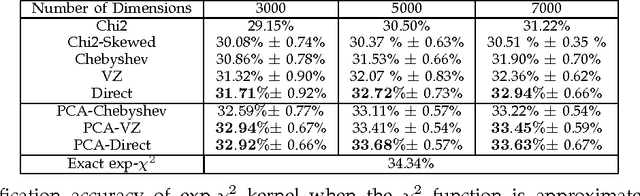
We propose a new analytical approximation to the $\chi^2$ kernel that converges geometrically. The analytical approximation is derived with elementary methods and adapts to the input distribution for optimal convergence rate. Experiments show the new approximation leads to improved performance in image classification and semantic segmentation tasks using a random Fourier feature approximation of the $\exp-\chi^2$ kernel. Besides, out-of-core principal component analysis (PCA) methods are introduced to reduce the dimensionality of the approximation and achieve better performance at the expense of only an additional constant factor to the time complexity. Moreover, when PCA is performed jointly on the training and unlabeled testing data, further performance improvements can be obtained. Experiments conducted on the PASCAL VOC 2010 segmentation and the ImageNet ILSVRC 2010 datasets show statistically significant improvements over alternative approximation methods.

The Manifold of Human Emotions

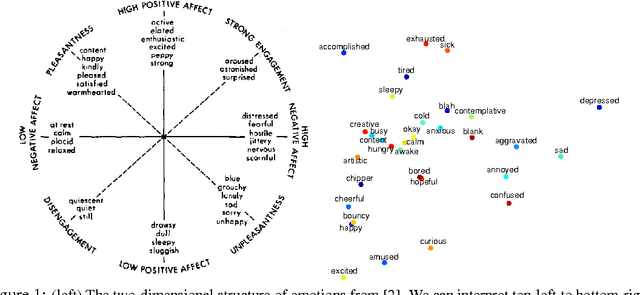
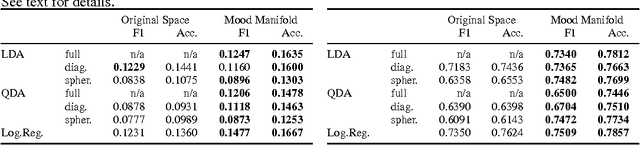
Sentiment analysis predicts the presence of positive or negative emotions in a text document. In this paper, we consider higher dimensional extensions of the sentiment concept, which represent a richer set of human emotions. Our approach goes beyond previous work in that our model contains a continuous manifold rather than a finite set of human emotions. We investigate the resulting model, compare it to psychological observations, and explore its predictive capabilities.

Matrix Approximation under Local Low-Rank Assumption

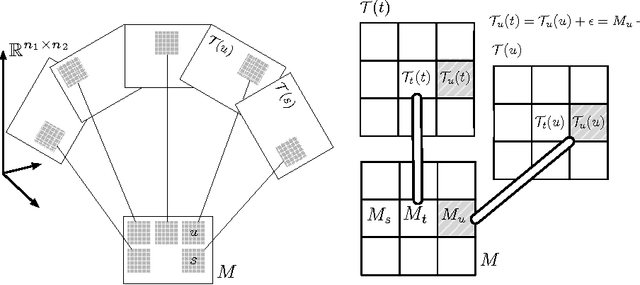
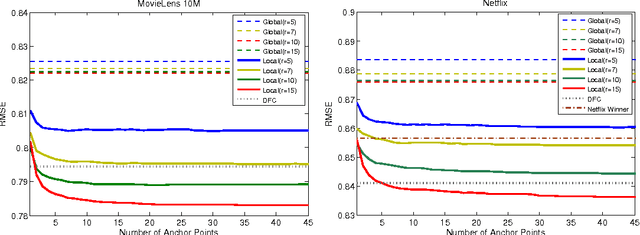
Matrix approximation is a common tool in machine learning for building accurate prediction models for recommendation systems, text mining, and computer vision. A prevalent assumption in constructing matrix approximations is that the partially observed matrix is of low-rank. We propose a new matrix approximation model where we assume instead that the matrix is only locally of low-rank, leading to a representation of the observed matrix as a weighted sum of low-rank matrices. We analyze the accuracy of the proposed local low-rank modeling. Our experiments show improvements in prediction accuracy in recommendation tasks.

Learning Riemannian Metrics

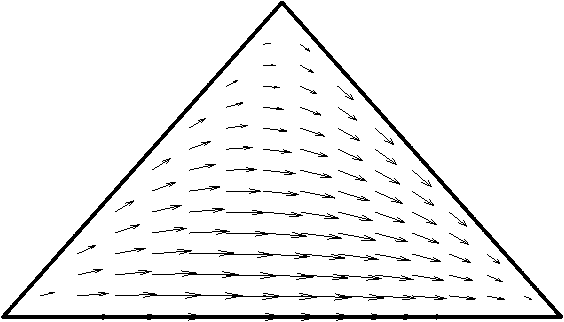
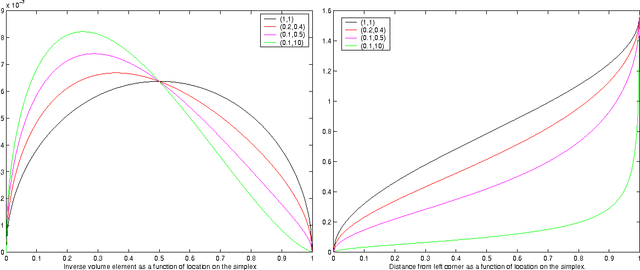
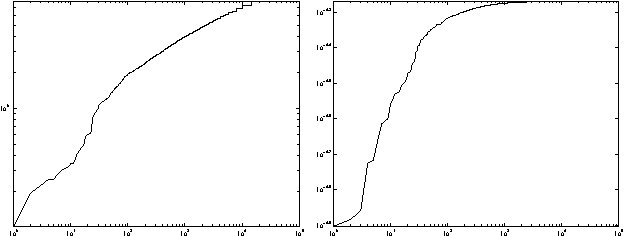
We propose a solution to the problem of estimating a Riemannian metric associated with a given differentiable manifold. The metric learning problem is based on minimizing the relative volume of a given set of points. We derive the details for a family of metrics on the multinomial simplex. The resulting metric has applications in text classification and bears some similarity to TFIDF representation of text documents.

Smooth Sparse Coding via Marginal Regression for Learning Sparse Representations

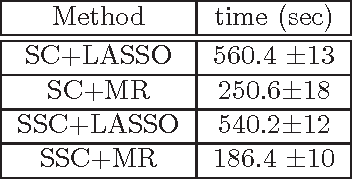
We propose and analyze a novel framework for learning sparse representations, based on two statistical techniques: kernel smoothing and marginal regression. The proposed approach provides a flexible framework for incorporating feature similarity or temporal information present in data sets, via non-parametric kernel smoothing. We provide generalization bounds for dictionary learning using smooth sparse coding and show how the sample complexity depends on the L1 norm of kernel function used. Furthermore, we propose using marginal regression for obtaining sparse codes, which significantly improves the speed and allows one to scale to large dictionary sizes easily. We demonstrate the advantages of the proposed approach, both in terms of accuracy and speed by extensive experimentation on several real data sets. In addition, we demonstrate how the proposed approach could be used for improving semi-supervised sparse coding.

An Extended Cencov-Campbell Characterization of Conditional Information Geometry

We formulate and prove an axiomatic characterization of conditional information geometry, for both the normalized and the nonnormalized cases. This characterization extends the axiomatic derivation of the Fisher geometry by Cencov and Campbell to the cone of positive conditional models, and as a special case to the manifold of conditional distributions. Due to the close connection between the conditional I-divergence and the product Fisher information metric the characterization provides a new axiomatic interpretation of the primal problems underlying logistic regression and AdaBoost.

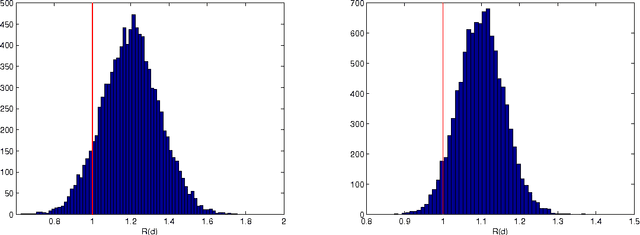
The Landmark Selection Method for Multiple Output Prediction

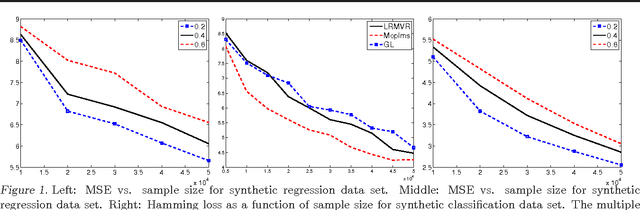
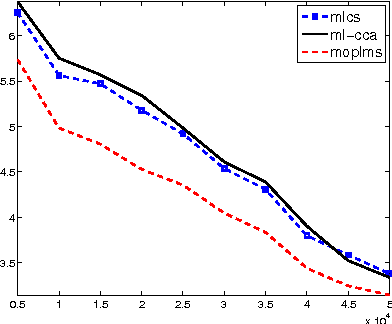
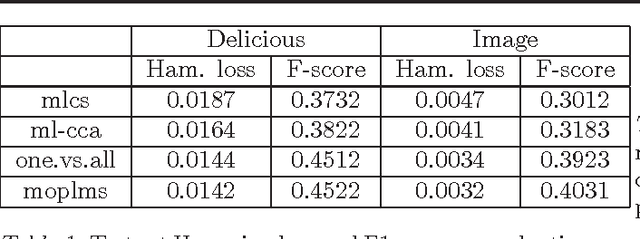
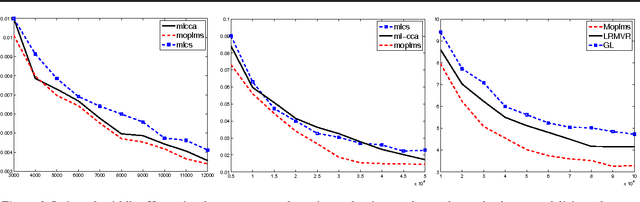
Conditional modeling x \to y is a central problem in machine learning. A substantial research effort is devoted to such modeling when x is high dimensional. We consider, instead, the case of a high dimensional y, where x is either low dimensional or high dimensional. Our approach is based on selecting a small subset y_L of the dimensions of y, and proceed by modeling (i) x \to y_L and (ii) y_L \to y. Composing these two models, we obtain a conditional model x \to y that possesses convenient statistical properties. Multi-label classification and multivariate regression experiments on several datasets show that this model outperforms the one vs. all approach as well as several sophisticated multiple output prediction methods.