Towards Explainable Automated Neuroanatomy

We present a novel method for quantifying the microscopic structure of brain tissue. It is based on the automated recognition of interpretable features obtained by analyzing the shapes of cells. This contrasts with prevailing methods of brain anatomical analysis in two ways. First, contemporary methods use gray-scale values derived from smoothed version of the anatomical images, which dissipated valuable information from the texture of the images. Second, contemporary analysis uses the output of black-box Convolutional Neural Networks, while our system makes decisions based on interpretable features obtained by analyzing the shapes of individual cells. An important benefit of this open-box approach is that the anatomist can understand and correct the decisions made by the computer. Our proposed system can accurately localize and identify existing brain structures. This can be used to align and coregistar brains and will facilitate connectomic studies for reverse engineering of brain circuitry.

Effective resistance in metric spaces

Effective resistance (ER) is an attractive way to interrogate the structure of graphs. It is an alternative to computing the eigenvectors of the graph Laplacian. One attractive application of ER is to point clouds, i.e. graphs whose vertices correspond to IID samples from a distribution over a metric space. Unfortunately, it was shown that the ER between any two points converges to a trivial quantity that holds no information about the graph's structure as the size of the sample increases to infinity. In this study, we show that this trivial solution can be circumvented by considering a region-based ER between pairs of small regions rather than pairs of points and by scaling the edge weights appropriately with respect to the underlying density in each region. By keeping the regions fixed, we show analytically that the region-based ER converges to a non-trivial limit as the number of points increases to infinity. Namely the ER on a metric space. We support our theoretical findings with numerical experiments.

Active learning using region-based sampling

We present a general-purpose active learning scheme for data in metric spaces. The algorithm maintains a collection of neighborhoods of different sizes and uses label queries to identify those that have a strong bias towards one particular label; when two such neighborhoods intersect and have different labels, the region of overlap is treated as a ``known unknown'' and is a target of future active queries. We give label complexity bounds for this method that do not rely on assumptions about the data and we instantiate them in several cases of interest.

Structure from Voltage

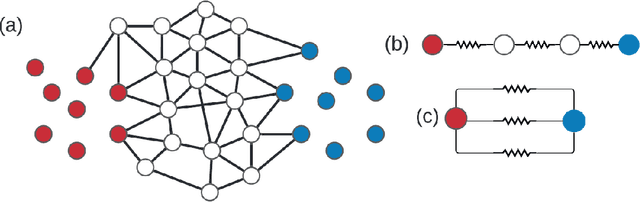
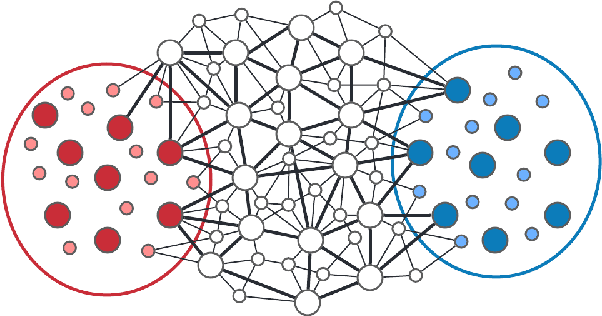
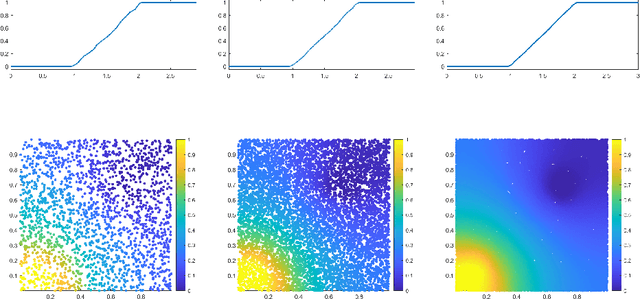
Effective resistance (ER) is an attractive way to interrogate the structure of graphs. It is an alternative to computing the eigen-vectors of the graph Laplacian. Graph laplacians are used to find low dimensional structures in high dimensional data. Here too, ER based analysis has advantages over eign-vector based methods. Unfortunately Von Luxburg et al. (2010) show that, when vertices correspond to a sample from a distribution over a metric space, the limit of the ER between distant points converges to a trivial quantity that holds no information about the structure of the graph. We show that by using scaling resistances in a graph with $n$ vertices by $n^2$, one gets a meaningful limit of the voltages and of effective resistances. We also show that by adding a "ground" node to a metric graph one gets a simple and natural way to compute all of the distances from a chosen point to all other points.

When is the Convergence Time of Langevin Algorithms Dimension Independent? A Composite Optimization Viewpoint

There has been a surge of works bridging MCMC sampling and optimization, with a specific focus on translating non-asymptotic convergence guarantees for optimization problems into the analysis of Langevin algorithms in MCMC sampling. A conspicuous distinction between the convergence analysis of Langevin sampling and that of optimization is that all known convergence rates for Langevin algorithms depend on the dimensionality of the problem, whereas the convergence rates for optimization are dimension-free for convex problems. Whether a dimension independent convergence rate can be achieved by Langevin algorithm is thus a long-standing open problem. This paper provides an affirmative answer to this problem for large classes of either Lipschitz or smooth convex problems with normal priors. By viewing Langevin algorithm as composite optimization, we develop a new analysis technique that leads to dimension independent convergence rates for such problems.

StreaMRAK a Streaming Multi-Resolution Adaptive Kernel Algorithm

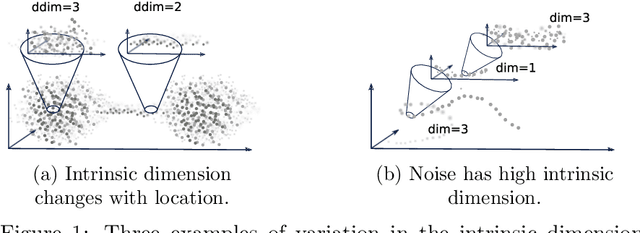
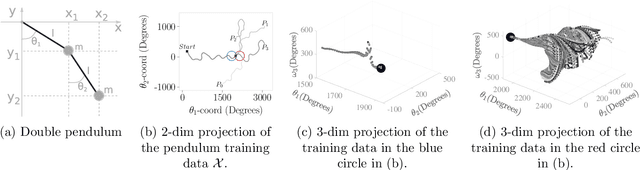
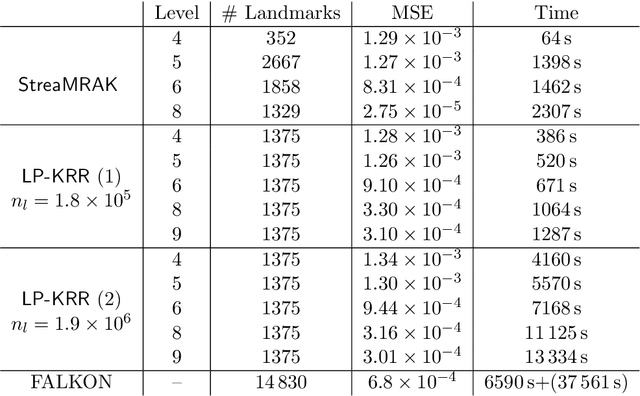
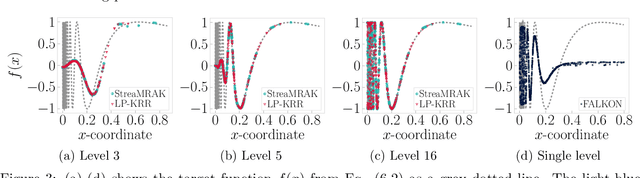
Kernel ridge regression (KRR) is a popular scheme for non-linear non-parametric learning. However, existing implementations of KRR require that all the data is stored in the main memory, which severely limits the use of KRR in contexts where data size far exceeds the memory size. Such applications are increasingly common in data mining, bioinformatics, and control. A powerful paradigm for computing on data sets that are too large for memory is the streaming model of computation, where we process one data sample at a time, discarding each sample before moving on to the next one. In this paper, we propose StreaMRAK - a streaming version of KRR. StreaMRAK improves on existing KRR schemes by dividing the problem into several levels of resolution, which allows continual refinement to the predictions. The algorithm reduces the memory requirement by continuously and efficiently integrating new samples into the training model. With a novel sub-sampling scheme, StreaMRAK reduces memory and computational complexities by creating a sketch of the original data, where the sub-sampling density is adapted to the bandwidth of the kernel and the local dimensionality of the data. We present a showcase study on two synthetic problems and the prediction of the trajectory of a double pendulum. The results show that the proposed algorithm is fast and accurate.

Optimal Strategies for Decision Theoretic Online Learning

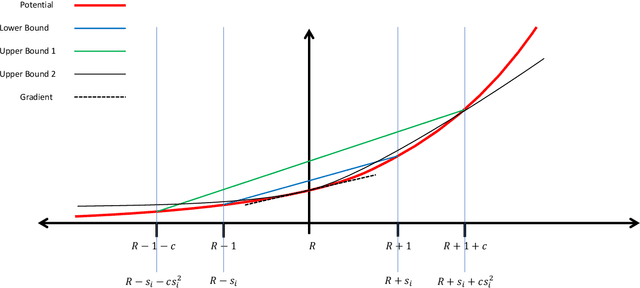
We extend the drifting games analysis to continuous time and show that the optimal adversary, if the value function has strictly positive derivative up to fourth order is bronian motion.

Audio scene monitoring using redundant un-localized microphone arrays

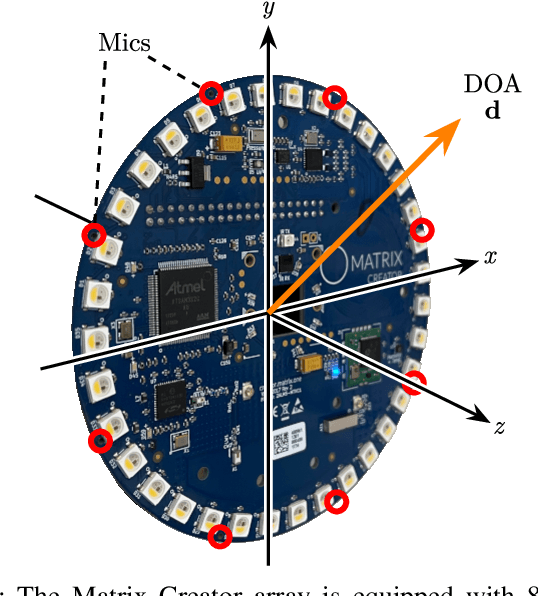
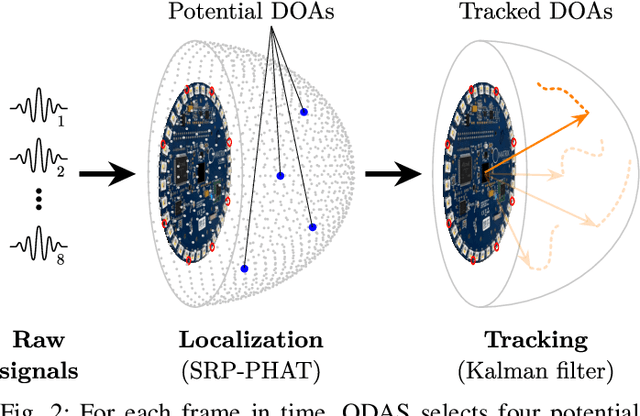
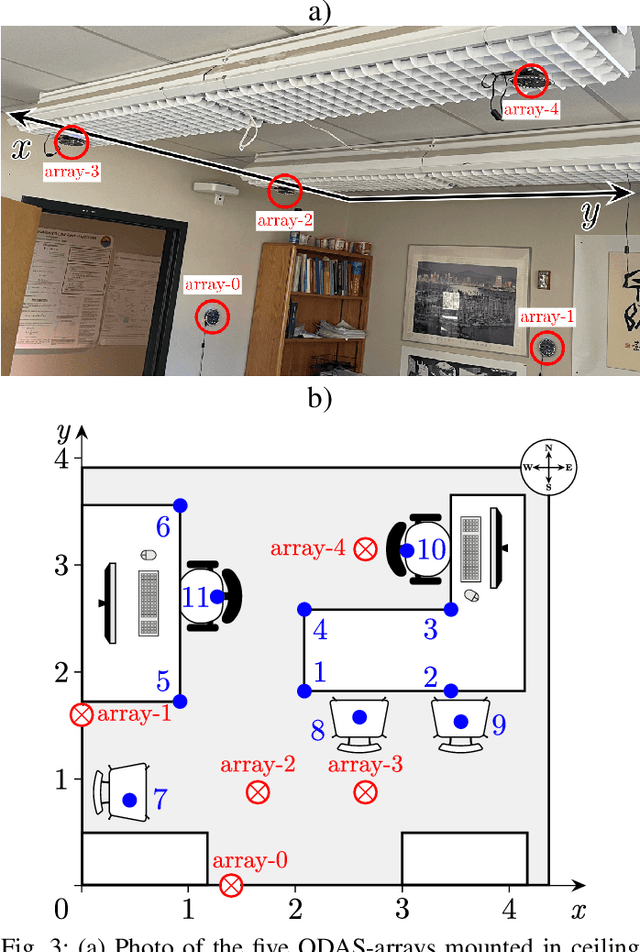
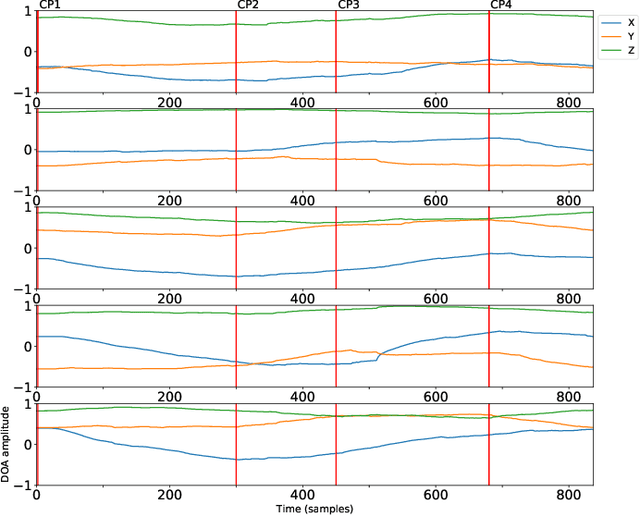
We present a system for localizing sound sources in a room with several microphone arrays. Unlike most existing approaches, the positions of the arrays in space are assumed to be unknown. Each circular array performs direction of arrival (DOA) estimation independently. The DOAs are then fed to a fusion center where they are concatenated and used to perform the localization based on two proposed methods, which require only few labeled source locations for calibration. The first proposed method is based on principal component analysis (PCA) of the observed DOA and does not require any calibration. The array cluster can then perform localization on a manifold defined by the PCA of concatenated DOAs over time. The second proposed method performs localization using an affine transformation between the DOA vectors and the room manifold. The PCA approach has fewer requirements on the training sequence, but is less robust to missing DOAs from one of the arrays. The approach is demonstrated with a set of five 8-microphone circular arrays, placed at unknown fixed locations in an office. Both the PCA approach and the direct approach can easily map out a rectangle based on a few calibration points with similar accuracy as calibration points. The methods demonstrated here provide a step towards monitoring activities in a smart home and require little installation effort as the array locations are not needed.

Experimental Design for Bathymetry Editing

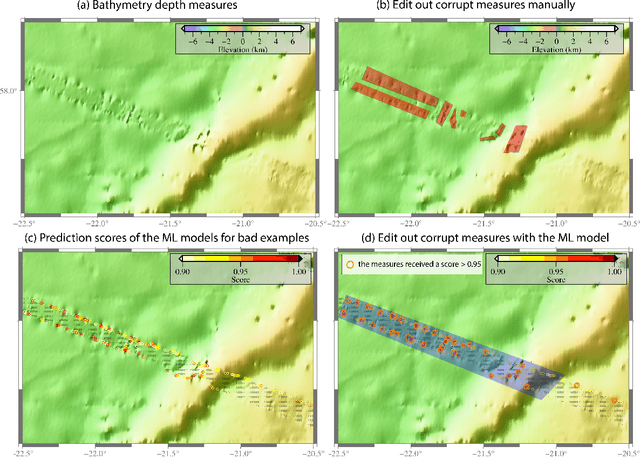
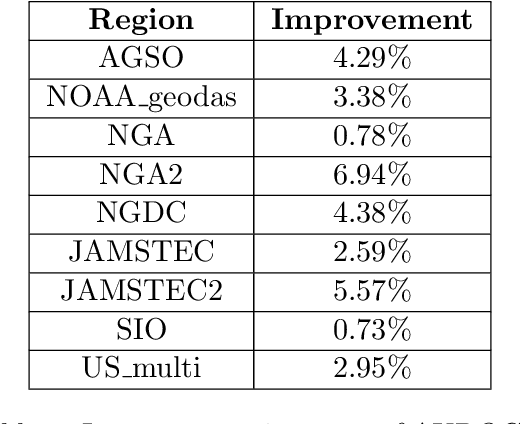
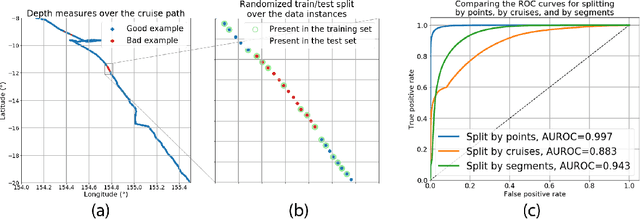
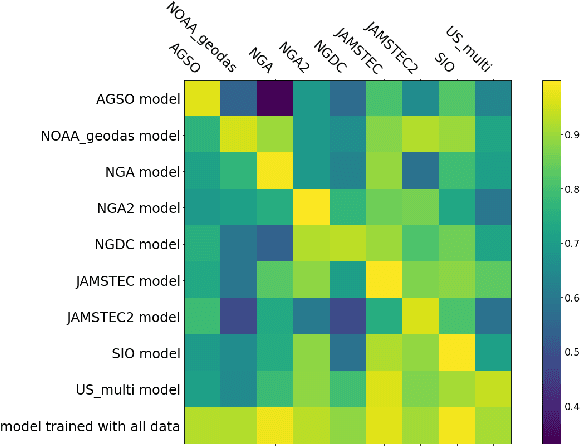
We describe an application of machine learning to a real-world computer assisted labeling task. Our experimental results expose significant deviations from the IID assumption commonly used in machine learning. These results suggest that the common random split of all data into training and testing can often lead to poor performance.

An adaptive nearest neighbor rule for classification

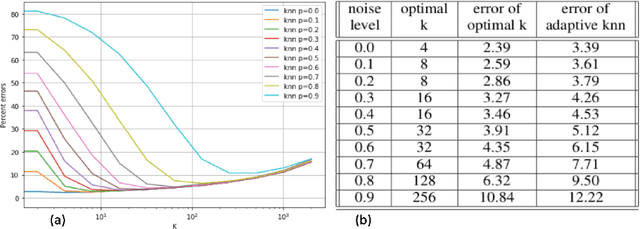
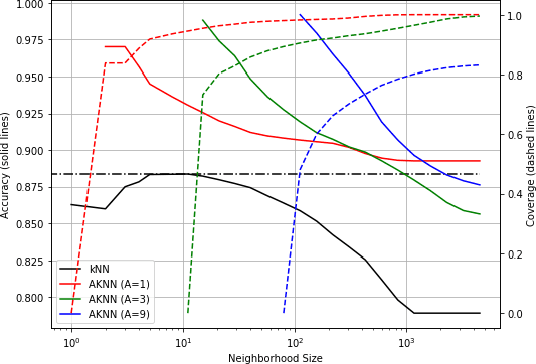
We introduce a variant of the $k$-nearest neighbor classifier in which $k$ is chosen adaptively for each query, rather than supplied as a parameter. The choice of $k$ depends on properties of each neighborhood, and therefore may significantly vary between different points. (For example, the algorithm will use larger $k$ for predicting the labels of points in noisy regions.) We provide theory and experiments that demonstrate that the algorithm performs comparably to, and sometimes better than, $k$-NN with an optimal choice of $k$. In particular, we derive bounds on the convergence rates of our classifier that depend on a local quantity we call the `advantage' which is significantly weaker than the Lipschitz conditions used in previous convergence rate proofs. These generalization bounds hinge on a variant of the seminal Uniform Convergence Theorem due to Vapnik and Chervonenkis; this variant concerns conditional probabilities and may be of independent interest.