How to safely discard features based on aggregate SHAP values

SHAP is one of the most popular local feature-attribution methods. Given a function f and an input x, it quantifies each feature's contribution to f(x). Recently, SHAP has been increasingly used for global insights: practitioners average the absolute SHAP values over many data points to compute global feature importance scores, which are then used to discard unimportant features. In this work, we investigate the soundness of this practice by asking whether small aggregate SHAP values necessarily imply that the corresponding feature does not affect the function. Unfortunately, the answer is no: even if the i-th SHAP value is 0 on the entire data support, there exist functions that clearly depend on Feature i. The issue is that computing SHAP values involves evaluating f on points outside of the data support, where f can be strategically designed to mask its dependence on Feature i. To address this, we propose to aggregate SHAP values over the extended support, which is the product of the marginals of the underlying distribution. With this modification, we show that a small aggregate SHAP value implies that we can safely discard the corresponding feature. We then extend our results to KernelSHAP, the most popular method to approximate SHAP values in practice. We show that if KernelSHAP is computed over the extended distribution, a small aggregate value justifies feature removal. This result holds independently of whether KernelSHAP accurately approximates true SHAP values, making it one of the first theoretical results to characterize the KernelSHAP algorithm itself. Our findings have both theoretical and practical implications. We introduce the Shapley Lie algebra, which offers algebraic insights that may enable a deeper investigation of SHAP and we show that randomly permuting each column of the data matrix enables safely discarding features based on aggregate SHAP and KernelSHAP values.

Auditing Local Explanations is Hard

In sensitive contexts, providers of machine learning algorithms are increasingly required to give explanations for their algorithms' decisions. However, explanation receivers might not trust the provider, who potentially could output misleading or manipulated explanations. In this work, we investigate an auditing framework in which a third-party auditor or a collective of users attempts to sanity-check explanations: they can query model decisions and the corresponding local explanations, pool all the information received, and then check for basic consistency properties. We prove upper and lower bounds on the amount of queries that are needed for an auditor to succeed within this framework. Our results show that successful auditing requires a potentially exorbitant number of queries -- particularly in high dimensional cases. Our analysis also reveals that a key property is the ``locality'' of the provided explanations -- a quantity that so far has not been paid much attention to in the explainability literature. Looking forward, our results suggest that for complex high-dimensional settings, merely providing a pointwise prediction and explanation could be insufficient, as there is no way for the users to verify that the provided explanations are not completely made-up.

Beyond Discrepancy: A Closer Look at the Theory of Distribution Shift

Many machine learning models appear to deploy effortlessly under distribution shift, and perform well on a target distribution that is considerably different from the training distribution. Yet, learning theory of distribution shift bounds performance on the target distribution as a function of the discrepancy between the source and target, rarely guaranteeing high target accuracy. Motivated by this gap, this work takes a closer look at the theory of distribution shift for a classifier from a source to a target distribution. Instead of relying on the discrepancy, we adopt an Invariant-Risk-Minimization (IRM)-like assumption connecting the distributions, and characterize conditions under which data from a source distribution is sufficient for accurate classification of the target. When these conditions are not met, we show when only unlabeled data from the target is sufficient, and when labeled target data is needed. In all cases, we provide rigorous theoretical guarantees in the large sample regime.

Effective resistance in metric spaces

Effective resistance (ER) is an attractive way to interrogate the structure of graphs. It is an alternative to computing the eigenvectors of the graph Laplacian. One attractive application of ER is to point clouds, i.e. graphs whose vertices correspond to IID samples from a distribution over a metric space. Unfortunately, it was shown that the ER between any two points converges to a trivial quantity that holds no information about the graph's structure as the size of the sample increases to infinity. In this study, we show that this trivial solution can be circumvented by considering a region-based ER between pairs of small regions rather than pairs of points and by scaling the edge weights appropriately with respect to the underlying density in each region. By keeping the regions fixed, we show analytically that the region-based ER converges to a non-trivial limit as the number of points increases to infinity. Namely the ER on a metric space. We support our theoretical findings with numerical experiments.

Data-Copying in Generative Models: A Formal Framework

There has been some recent interest in detecting and addressing memorization of training data by deep neural networks. A formal framework for memorization in generative models, called "data-copying," was proposed by Meehan et. al. (2020). We build upon their work to show that their framework may fail to detect certain kinds of blatant memorization. Motivated by this and the theory of non-parametric methods, we provide an alternative definition of data-copying that applies more locally. We provide a method to detect data-copying, and provably show that it works with high probability when enough data is available. We also provide lower bounds that characterize the sample requirement for reliable detection.

Robust Empirical Risk Minimization with Tolerance

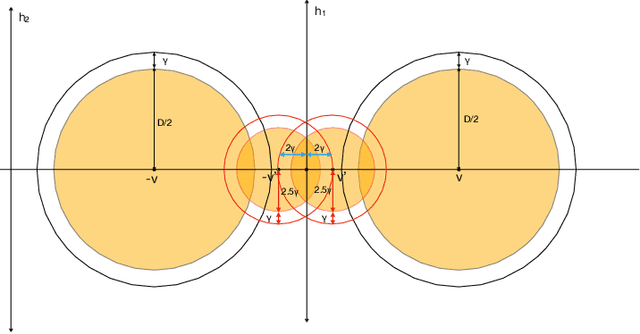
Developing simple, sample-efficient learning algorithms for robust classification is a pressing issue in today's tech-dominated world, and current theoretical techniques requiring exponential sample complexity and complicated improper learning rules fall far from answering the need. In this work we study the fundamental paradigm of (robust) $\textit{empirical risk minimization}$ (RERM), a simple process in which the learner outputs any hypothesis minimizing its training error. RERM famously fails to robustly learn VC classes (Montasser et al., 2019a), a bound we show extends even to `nice' settings such as (bounded) halfspaces. As such, we study a recent relaxation of the robust model called $\textit{tolerant}$ robust learning (Ashtiani et al., 2022) where the output classifier is compared to the best achievable error over slightly larger perturbation sets. We show that under geometric niceness conditions, a natural tolerant variant of RERM is indeed sufficient for $\gamma$-tolerant robust learning VC classes over $\mathbb{R}^d$, and requires only $\tilde{O}\left( \frac{VC(H)d\log \frac{D}{\gamma\delta}}{\epsilon^2}\right)$ samples for robustness regions of (maximum) diameter $D$.

Structure from Voltage

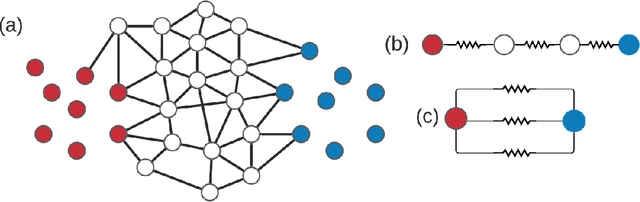
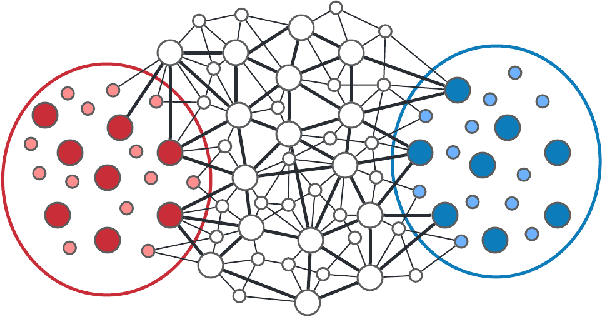
Effective resistance (ER) is an attractive way to interrogate the structure of graphs. It is an alternative to computing the eigen-vectors of the graph Laplacian. Graph laplacians are used to find low dimensional structures in high dimensional data. Here too, ER based analysis has advantages over eign-vector based methods. Unfortunately Von Luxburg et al. (2010) show that, when vertices correspond to a sample from a distribution over a metric space, the limit of the ER between distant points converges to a trivial quantity that holds no information about the structure of the graph. We show that by using scaling resistances in a graph with $n$ vertices by $n^2$, one gets a meaningful limit of the voltages and of effective resistances. We also show that by adding a "ground" node to a metric graph one gets a simple and natural way to compute all of the distances from a chosen point to all other points.

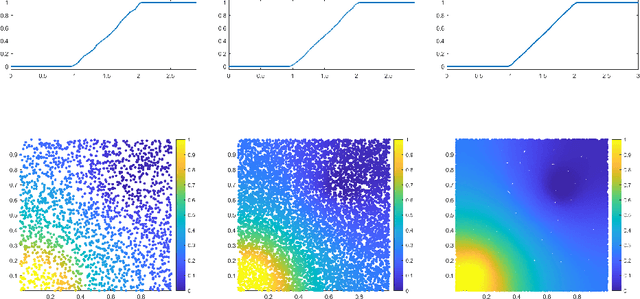
An Exploration of Multicalibration Uniform Convergence Bounds

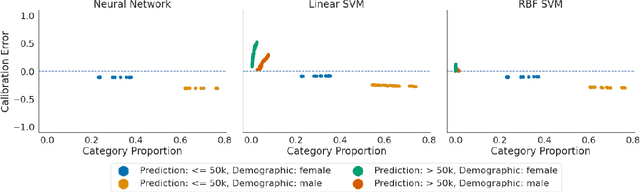
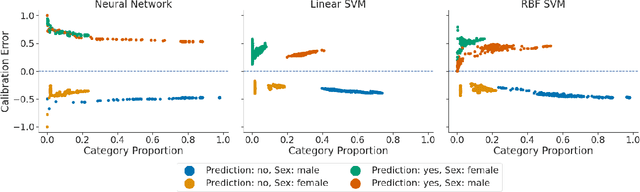
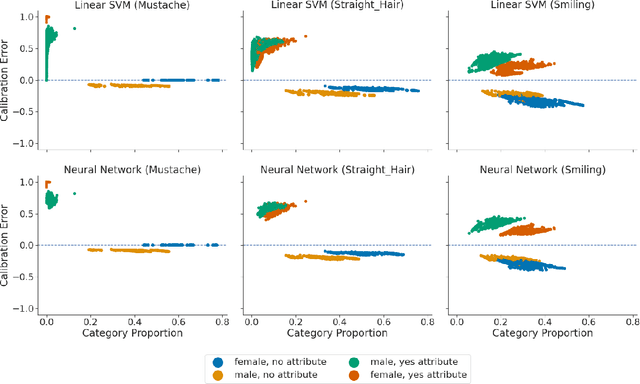
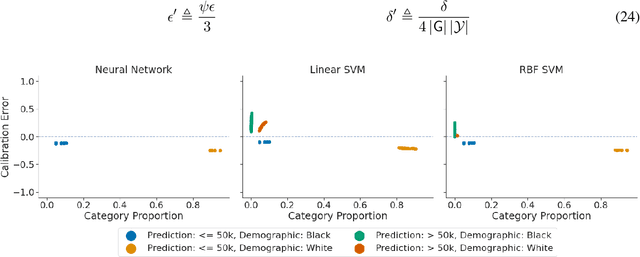
Recent works have investigated the sample complexity necessary for fair machine learning. The most advanced of such sample complexity bounds are developed by analyzing multicalibration uniform convergence for a given predictor class. We present a framework which yields multicalibration error uniform convergence bounds by reparametrizing sample complexities for Empirical Risk Minimization (ERM) learning. From this framework, we demonstrate that multicalibration error exhibits dependence on the classifier architecture as well as the underlying data distribution. We perform an experimental evaluation to investigate the behavior of multicalibration error for different families of classifiers. We compare the results of this evaluation to multicalibration error concentration bounds. Our investigation provides additional perspective on both algorithmic fairness and multicalibration error convergence bounds. Given the prevalence of ERM sample complexity bounds, our proposed framework enables machine learning practitioners to easily understand the convergence behavior of multicalibration error for a myriad of classifier architectures.

Learning what to remember

We consider a lifelong learning scenario in which a learner faces a neverending and arbitrary stream of facts and has to decide which ones to retain in its limited memory. We introduce a mathematical model based on the online learning framework, in which the learner measures itself against a collection of experts that are also memory-constrained and that reflect different policies for what to remember. Interspersed with the stream of facts are occasional questions, and on each of these the learner incurs a loss if it has not remembered the corresponding fact. Its goal is to do almost as well as the best expert in hindsight, while using roughly the same amount of memory. We identify difficulties with using the multiplicative weights update algorithm in this memory-constrained scenario, and design an alternative scheme whose regret guarantees are close to the best possible.

No-Substitution $k$-means Clustering with Low Center Complexity and Memory

Clustering is a fundamental task in machine learning. Given a dataset $X = \{x_1, \ldots x_n\}$, the goal of $k$-means clustering is to pick $k$ "centers" from $X$ in a way that minimizes the sum of squared distances from each point to its nearest center. We consider $k$-means clustering in the online, no substitution setting, where one must decide whether to take $x_t$ as a center immediately upon streaming it and cannot remove centers once taken. The online, no substitution setting is challenging for clustering--one can show that there exist datasets $X$ for which any $O(1)$-approximation $k$-means algorithm must have center complexity $\Omega(n)$, meaning that it takes $\Omega(n)$ centers in expectation. Bhattacharjee and Moshkovitz (2020) refined this bound by defining a complexity measure called $Lower_{\alpha, k}(X)$, and proving that any $\alpha$-approximation algorithm must have center complexity $\Omega(Lower_{\alpha, k}(X))$. They then complemented their lower bound by giving a $O(k^3)$-approximation algorithm with center complexity $\tilde{O}(k^2Lower_{k^3, k}(X))$, thus showing that their parameter is a tight measure of required center complexity. However, a major drawback of their algorithm is its memory requirement, which is $O(n)$. This makes the algorithm impractical for very large datasets. In this work, we strictly improve upon their algorithm on all three fronts; we develop a $36$-approximation algorithm with center complexity $\tilde{O}(kLower_{36, k}(X))$ that uses only $O(k)$ additional memory. In addition to having nearly optimal memory, this algorithm is the first known algorithm with center complexity bounded by $Lower_{36, k}(X)$ that is a true $O(1)$-approximation with its approximation factor being independent of $k$ or $n$.