Effective resistance in metric spaces

Effective resistance (ER) is an attractive way to interrogate the structure of graphs. It is an alternative to computing the eigenvectors of the graph Laplacian. One attractive application of ER is to point clouds, i.e. graphs whose vertices correspond to IID samples from a distribution over a metric space. Unfortunately, it was shown that the ER between any two points converges to a trivial quantity that holds no information about the graph's structure as the size of the sample increases to infinity. In this study, we show that this trivial solution can be circumvented by considering a region-based ER between pairs of small regions rather than pairs of points and by scaling the edge weights appropriately with respect to the underlying density in each region. By keeping the regions fixed, we show analytically that the region-based ER converges to a non-trivial limit as the number of points increases to infinity. Namely the ER on a metric space. We support our theoretical findings with numerical experiments.

StreaMRAK a Streaming Multi-Resolution Adaptive Kernel Algorithm

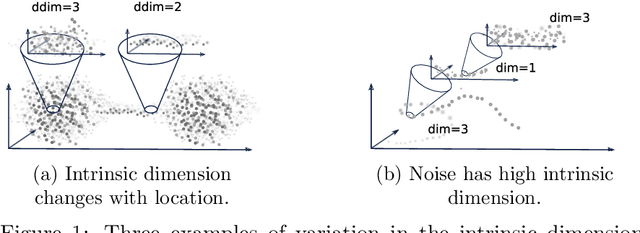
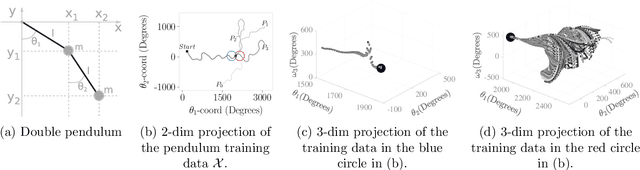
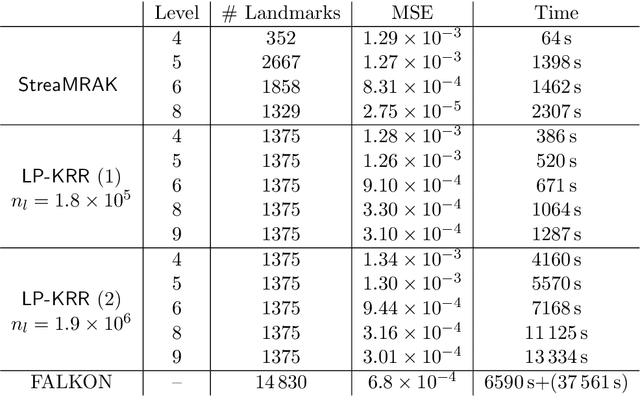
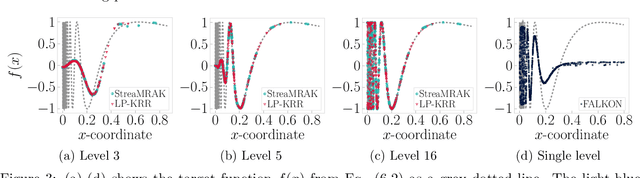
Kernel ridge regression (KRR) is a popular scheme for non-linear non-parametric learning. However, existing implementations of KRR require that all the data is stored in the main memory, which severely limits the use of KRR in contexts where data size far exceeds the memory size. Such applications are increasingly common in data mining, bioinformatics, and control. A powerful paradigm for computing on data sets that are too large for memory is the streaming model of computation, where we process one data sample at a time, discarding each sample before moving on to the next one. In this paper, we propose StreaMRAK - a streaming version of KRR. StreaMRAK improves on existing KRR schemes by dividing the problem into several levels of resolution, which allows continual refinement to the predictions. The algorithm reduces the memory requirement by continuously and efficiently integrating new samples into the training model. With a novel sub-sampling scheme, StreaMRAK reduces memory and computational complexities by creating a sketch of the original data, where the sub-sampling density is adapted to the bandwidth of the kernel and the local dimensionality of the data. We present a showcase study on two synthetic problems and the prediction of the trajectory of a double pendulum. The results show that the proposed algorithm is fast and accurate.