GeoEdit: Local Frames for Fast, Training-Free On-Manifold Editing in Diffusion Models

Diffusion models are a leading paradigm for data generation, but training-free editing typically re-runs the full denoising trajectory for every edit strength, making iterative refinement expensive. To address this issue, we instead edit near the data manifold, where small local updates can replace repeated re-synthesis. To enable this, we estimate a local manifold tangent space directly from perturbed samples and prove that this sample-based estimator closely approximates the true tangent. Building on this guarantee, we devise a Jacobian-free algorithm that constructs a tangent frame via small perturbations to the initial noise and alternates small tangent moves with diffusion-based projections. Updates within this frame follow principled on-manifold directions while suppressing off-manifold drift, enabling fine-grained edits without full re-diffusion or additional training. Edit strength is controlled by the number of steps for rapid, continuous adjustments that preserve fidelity and plug into existing samplers. Empirically, the resulting tangent directions yield smooth, semantic unsupervised traversals and effective CLIP-guided optimization, demonstrating practical interactive continuous editing.

Unbalanced Optimal Transport Dictionary Learning for Unsupervised Hyperspectral Image Clustering

Hyperspectral images capture vast amounts of high-dimensional spectral information about a scene, making labeling an intensive task that is resistant to out-of-the-box statistical methods. Unsupervised learning of clusters allows for automated segmentation of the scene, enabling a more rapid understanding of the image. Partitioning the spectral information contained within the data via dictionary learning in Wasserstein space has proven an effective method for unsupervised clustering. However, this approach requires balancing the spectral profiles of the data, blurring the classes, and sacrificing robustness to outliers and noise. In this paper, we suggest improving this approach by utilizing unbalanced Wasserstein barycenters to learn a lower-dimensional representation of the underlying data. The deployment of spectral clustering on the learned representation results in an effective approach for the unsupervised learning of labels.

OT Score: An OT based Confidence Score for Unsupervised Domain Adaptation

We address the computational and theoretical limitations of existing distributional alignment methods for unsupervised domain adaptation (UDA), particularly regarding the estimation of classification performance and confidence without target labels. Current theoretical frameworks for these methods often yield computationally intractable quantities and fail to adequately reflect the properties of the alignment algorithms employed. To overcome these challenges, we introduce the Optimal Transport (OT) score, a confidence metric derived from a novel theoretical analysis that exploits the flexibility of decision boundaries induced by Semi-Discrete Optimal Transport alignment. The proposed OT score is intuitively interpretable, theoretically rigorous, and computationally efficient. It provides principled uncertainty estimates for any given set of target pseudo-labels without requiring model retraining, and can flexibly adapt to varying degrees of available source information. Experimental results on standard UDA benchmarks demonstrate that classification accuracy consistently improves by identifying and removing low-confidence predictions, and that OT score significantly outperforms existing confidence metrics across diverse adaptation scenarios.

Structure from Voltage

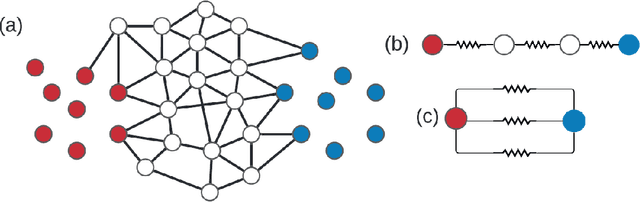
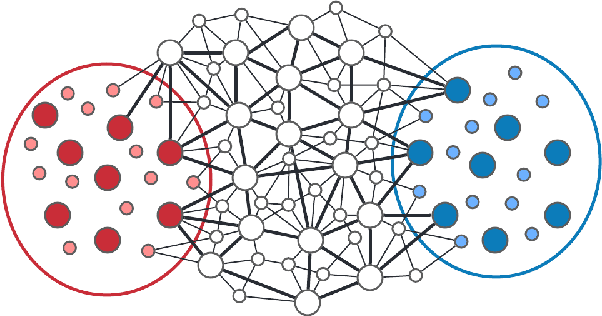
Effective resistance (ER) is an attractive way to interrogate the structure of graphs. It is an alternative to computing the eigen-vectors of the graph Laplacian. Graph laplacians are used to find low dimensional structures in high dimensional data. Here too, ER based analysis has advantages over eign-vector based methods. Unfortunately Von Luxburg et al. (2010) show that, when vertices correspond to a sample from a distribution over a metric space, the limit of the ER between distant points converges to a trivial quantity that holds no information about the structure of the graph. We show that by using scaling resistances in a graph with $n$ vertices by $n^2$, one gets a meaningful limit of the voltages and of effective resistances. We also show that by adding a "ground" node to a metric graph one gets a simple and natural way to compute all of the distances from a chosen point to all other points.

Nonclosedness of the Set of Neural Networks in Sobolev Space

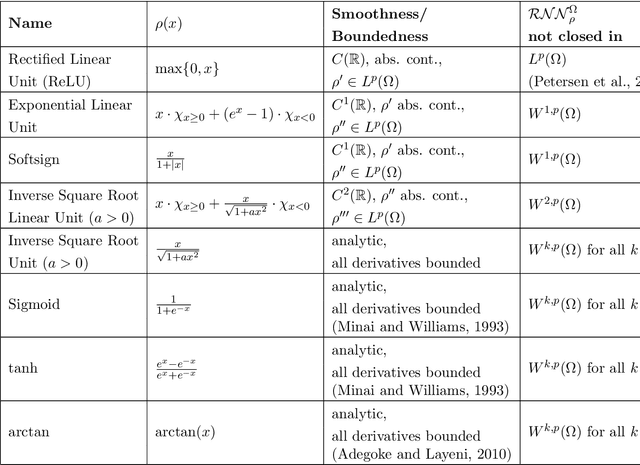
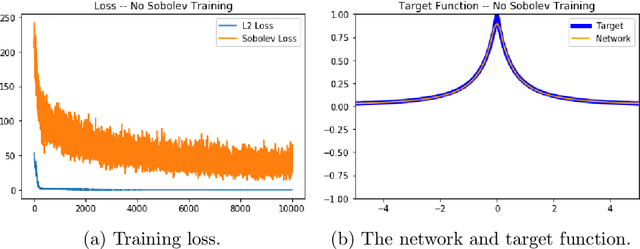
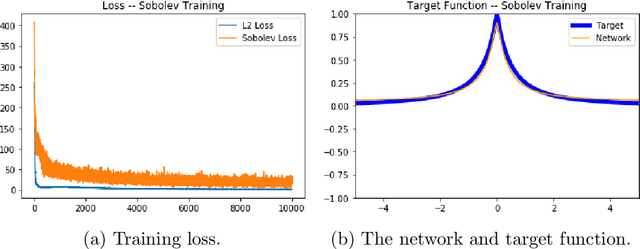
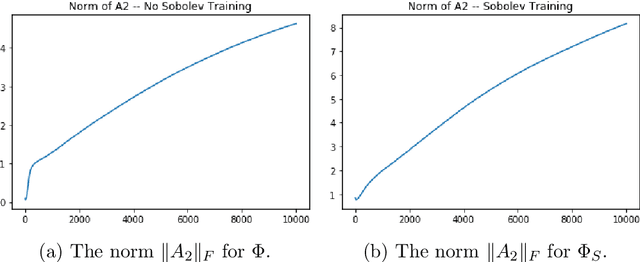
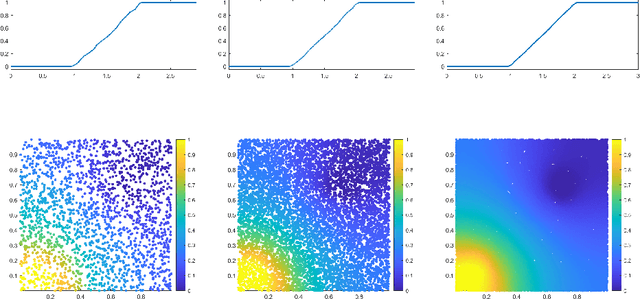
We examine the closedness of the set of realized neural networks of a fixed architecture in Sobolev space. For an exactly $m$-times differentiable activation function $\rho$, we construct a sequence of neural networks $(\Phi_n)_{n \in \mathbb{N}}$ whose realizations converge in order-$(m-1)$ Sobolev norm to a function that cannot be realized exactly by a neural network. Thus, the set of realized neural networks is not closed in the order-$(m-1)$ Sobolev space $W^{m-1,p}$. We further show that this set is not closed in $W^{m,p}$ under slightly stronger conditions on the $m$-th derivative of $\rho$. For a real analytic activation function, we show that the set of realized neural networks is not closed in $W^{k,p}$ for any $k \in \mathbb{N}$. These results suggest that training a network to approximate a target function in Sobolev norm does not prevent parameter explosion. Finally, we present experimental results demonstrating that parameter explosion occurs in stochastic training regardless of the norm under which the network is trained. However, the network is still capable of closely approximating a non-network target function with network parameters that grow at a manageable rate.

Defending against Adversarial Images using Basis Functions Transformations

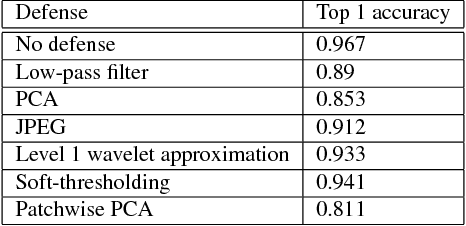
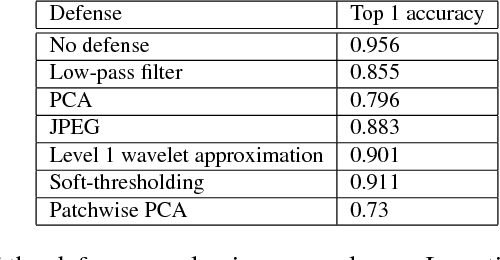
We study the effectiveness of various approaches that defend against adversarial attacks on deep networks via manipulations based on basis function representations of images. Specifically, we experiment with low-pass filtering, PCA, JPEG compression, low resolution wavelet approximation, and soft-thresholding. We evaluate these defense techniques using three types of popular attacks in black, gray and white-box settings. Our results show JPEG compression tends to outperform the other tested defenses in most of the settings considered, in addition to soft-thresholding, which performs well in specific cases, and yields a more mild decrease in accuracy on benign examples. In addition, we also mathematically derive a novel white-box attack in which the adversarial perturbation is composed only of terms corresponding a to pre-determined subset of the basis functions, of which a "low frequency attack" is a special case.