Denoising guarantees for optimized sampling schemes in compressed sensing

Compressed sensing with subsampled unitary matrices benefits from \emph{optimized} sampling schemes, which feature improved theoretical guarantees and empirical performance relative to uniform subsampling. We provide, in a first of its kind in compressed sensing, theoretical guarantees showing that the error caused by the measurement noise vanishes with an increasing number of measurements for optimized sampling schemes, assuming that the noise is Gaussian. We moreover provide similar guarantees for measurements sampled with-replacement with arbitrary probability weights. All our results hold on prior sets contained in a union of low-dimensional subspaces. Finally, we demonstrate that this denoising behavior appears in empirical experiments with a rate that closely matches our theoretical guarantees when the prior set is the range of a generative ReLU neural network and when it is the set of sparse vectors.

Model-adapted Fourier sampling for generative compressed sensing

We study generative compressed sensing when the measurement matrix is randomly subsampled from a unitary matrix (with the DFT as an important special case). It was recently shown that $\textit{O}(kdn\| \boldsymbol{\alpha}\|_{\infty}^{2})$ uniformly random Fourier measurements are sufficient to recover signals in the range of a neural network $G:\mathbb{R}^k \to \mathbb{R}^n$ of depth $d$, where each component of the so-called local coherence vector $\boldsymbol{\alpha}$ quantifies the alignment of a corresponding Fourier vector with the range of $G$. We construct a model-adapted sampling strategy with an improved sample complexity of $\textit{O}(kd\| \boldsymbol{\alpha}\|_{2}^{2})$ measurements. This is enabled by: (1) new theoretical recovery guarantees that we develop for nonuniformly random sampling distributions and then (2) optimizing the sampling distribution to minimize the number of measurements needed for these guarantees. This development offers a sample complexity applicable to natural signal classes, which are often almost maximally coherent with low Fourier frequencies. Finally, we consider a surrogate sampling scheme, and validate its performance in recovery experiments using the CelebA dataset.

A coherence parameter characterizing generative compressed sensing with Fourier measurements

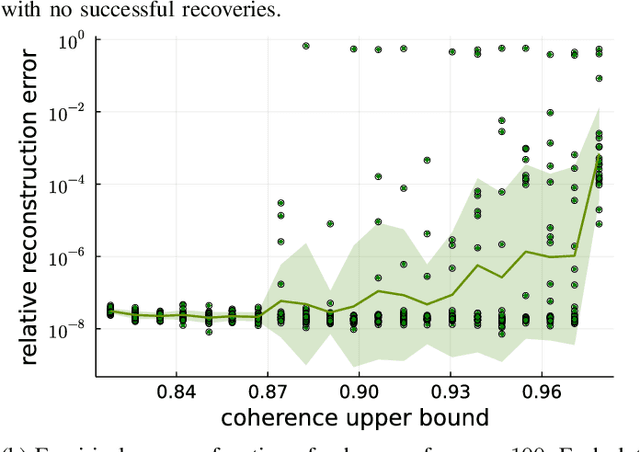
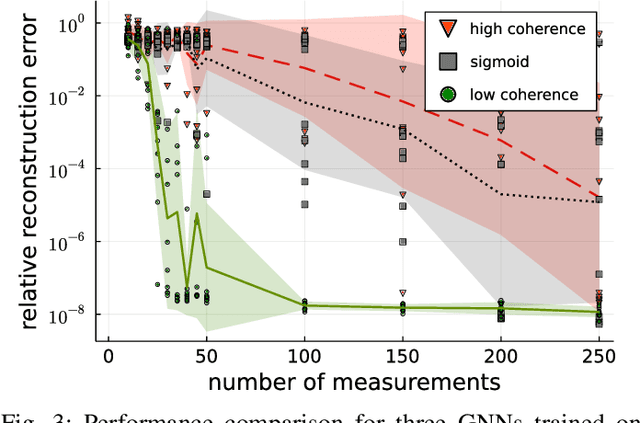
In Bora et al. (2017), a mathematical framework was developed for compressed sensing guarantees in the setting where the measurement matrix is Gaussian and the signal structure is the range of a generative neural network (GNN). The problem of compressed sensing with GNNs has since been extensively analyzed when the measurement matrix and/or network weights follow a subgaussian distribution. We move beyond the subgaussian assumption, to measurement matrices that are derived by sampling uniformly at random rows of a unitary matrix (including subsampled Fourier measurements as a special case). Specifically, we prove the first known restricted isometry guarantee for generative compressed sensing with subsampled isometries, and provide recovery bounds with nearly order-optimal sample complexity, addressing an open problem of Scarlett et al. (2022, p. 10). Recovery efficacy is characterized by the coherence, a new parameter, which measures the interplay between the range of the network and the measurement matrix. Our approach relies on subspace counting arguments and ideas central to high-dimensional probability. Furthermore, we propose a regularization strategy for training GNNs to have favourable coherence with the measurement operator. We provide compelling numerical simulations that support this regularized training strategy: our strategy yields low coherence networks that require fewer measurements for signal recovery. This, together with our theoretical results, supports coherence as a natural quantity for characterizing generative compressed sensing with subsampled isometries.

Beyond Independent Measurements: General Compressed Sensing with GNN Application

We consider the problem of recovering a structured signal $\mathbf{x} \in \mathbb{R}^{n}$ from noisy linear observations $\mathbf{y} =\mathbf{M} \mathbf{x}+\mathbf{w}$. The measurement matrix is modeled as $\mathbf{M} = \mathbf{B}\mathbf{A}$, where $\mathbf{B} \in \mathbb{R}^{l \times m}$ is arbitrary and $\mathbf{A} \in \mathbb{R}^{m \times n}$ has independent sub-gaussian rows. By varying $\mathbf{B}$, and the sub-gaussian distribution of $\mathbf{A}$, this gives a family of measurement matrices which may have heavy tails, dependent rows and columns, and singular values with a large dynamic range. When the structure is given as a possibly non-convex cone $T \subset \mathbb{R}^{n}$, an approximate empirical risk minimizer is proven to be a robust estimator if the effective number of measurements is sufficient, even in the presence of a model mismatch. In classical compressed sensing with independent (sub-)gaussian measurements, one asks how many measurements are needed to recover $\mathbf{x}$? In our setting, however, the effective number of measurements depends on the properties of $\mathbf{B}$. We show that the effective rank of $\mathbf{B}$ may be used as a surrogate for the number of measurements, and if this exceeds the squared Gaussian mean width of $(T-T) \cap \mathbb{S}^{n-1}$, then accurate recovery is guaranteed. Furthermore, we examine the special case of generative priors in detail, that is when $\mathbf{x}$ lies close to $T = \mathrm{ran}(G)$ and $G: \mathbb{R}^k \rightarrow \mathbb{R}^n$ is a Generative Neural Network (GNN) with ReLU activation functions. Our work relies on a recent result in random matrix theory by Jeong, Li, Plan, and Yilmaz arXiv:2001.10631. .

Sub-Gaussian Matrices on Sets: Optimal Tail Dependence and Applications

Random linear mappings are widely used in modern signal processing, compressed sensing and machine learning. These mappings may be used to embed the data into a significantly lower dimension while at the same time preserving useful information. This is done by approximately preserving the distances between data points, which are assumed to belong to $\mathbb{R}^n$. Thus, the performance of these mappings is usually captured by how close they are to an isometry on the data. Random Gaussian linear mappings have been the object of much study, while the sub-Gaussian settings is not yet fully understood. In the latter case, the performance depends on the sub-Gaussian norm of the rows. In many applications, e.g., compressed sensing, this norm may be large, or even growing with dimension, and thus it is important to characterize this dependence. We study when a sub-Gaussian matrix can become a near isometry on a set, show that previous best known dependence on the sub-Gaussian norm was sub-optimal, and present the optimal dependence. Our result not only answers a remaining question posed by Liaw, Mehrabian, Plan and Vershynin in 2017, but also generalizes their work. We also develop a new Bernstein type inequality for sub-exponential random variables, and a new Hanson-Wright inequality for quadratic forms of sub-Gaussian random variables, in both cases improving the bounds in the sub-Gaussian regime under moment constraints. Finally, we illustrate popular applications such as Johnson-Lindenstrauss embeddings, randomized sketches and blind demodulation, whose theoretical guarantees can be improved by our results in the sub-Gaussian case.

Tight Analyses for Non-Smooth Stochastic Gradient Descent

Consider the problem of minimizing functions that are Lipschitz and strongly convex, but not necessarily differentiable. We prove that after $T$ steps of stochastic gradient descent, the error of the final iterate is $O(\log(T)/T)$ with high probability. We also construct a function from this class for which the error of the final iterate of deterministic gradient descent is $\Omega(\log(T)/T)$. This shows that the upper bound is tight and that, in this setting, the last iterate of stochastic gradient descent has the same general error rate (with high probability) as deterministic gradient descent. This resolves both open questions posed by Shamir (2012). An intermediate step of our analysis proves that the suffix averaging method achieves error $O(1/T)$ with high probability, which is optimal (for any first-order optimization method). This improves results of Rakhlin (2012) and Hazan and Kale (2014), both of which achieved error $O(1/T)$, but only in expectation, and achieved a high probability error bound of $O(\log \log(T)/T)$, which is suboptimal. We prove analogous results for functions that are Lipschitz and convex, but not necessarily strongly convex or differentiable. After $T$ steps of stochastic gradient descent, the error of the final iterate is $O(\log(T)/\sqrt{T})$ with high probability, and there exists a function for which the error of the final iterate of deterministic gradient descent is $\Omega(\log(T)/\sqrt{T})$.

Settling the Sample Complexity for Learning Mixtures of Gaussians

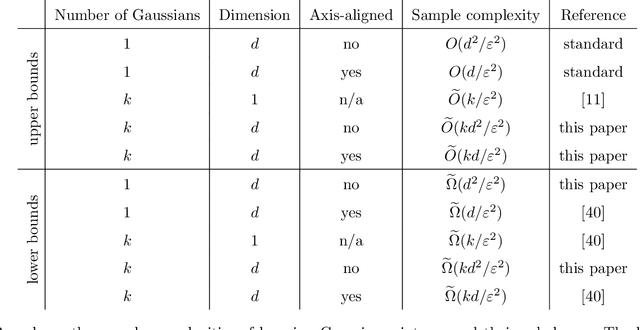
We prove that $\widetilde{\Theta}(k d^2 / \varepsilon^2)$ samples are necessary and sufficient for learning a mixture of $k$ Gaussians in $\mathbf{R}^d$, up to error $\varepsilon$ in total variation distance. This improves both the known upper bound and lower bound for this problem. For mixtures of axis-aligned Gaussians, we show that $\widetilde{O}(k d / \varepsilon^2)$ samples suffice, matching a known lower bound. Moreover, these results hold in an agnostic learning setting as well. The upper bound is based on a novel technique for distribution learning based on a notion of sample compression. Any class of distributions that allows such a sample compression scheme can also be learned with few samples. Moreover, if a class of distributions has such a compression scheme, then so do the classes of products and mixtures of those distributions. The core of our main result is showing that the class of Gaussians in $\mathbf{R}^d$ has an efficient sample compression.

Near-optimal sample complexity for convex tensor completion

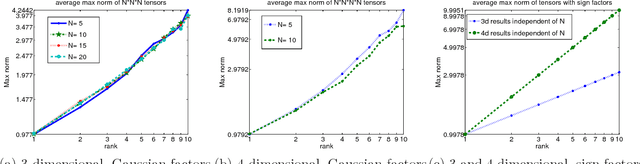
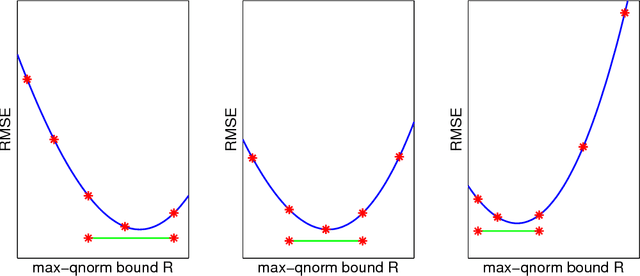
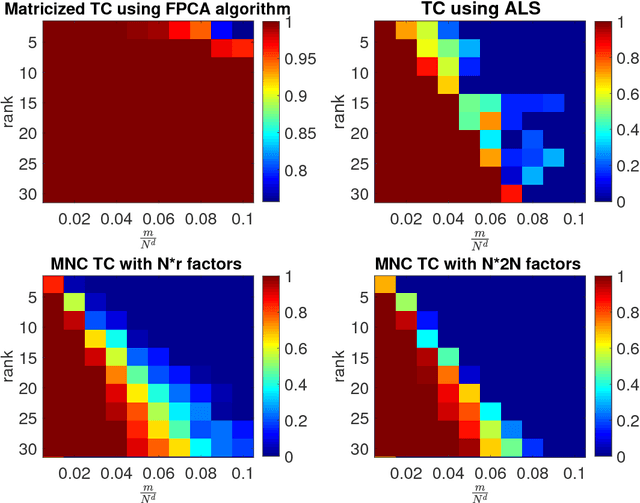
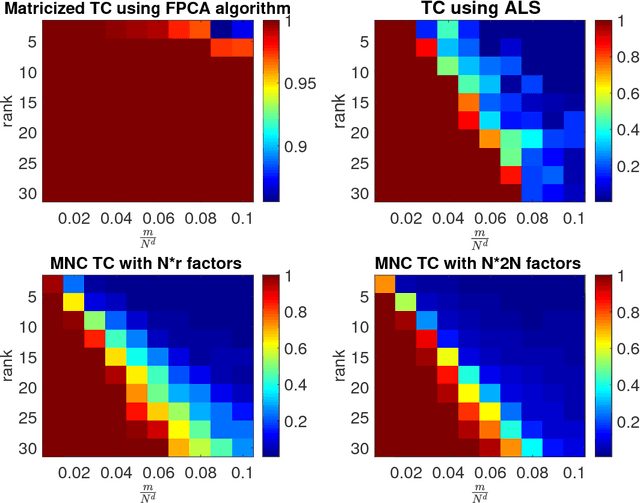
We analyze low rank tensor completion (TC) using noisy measurements of a subset of the tensor. Assuming a rank-$r$, order-$d$, $N \times N \times \cdots \times N$ tensor where $r=O(1)$, the best sampling complexity that was achieved is $O(N^{\frac{d}{2}})$, which is obtained by solving a tensor nuclear-norm minimization problem. However, this bound is significantly larger than the number of free variables in a low rank tensor which is $O(dN)$. In this paper, we show that by using an atomic-norm whose atoms are rank-$1$ sign tensors, one can obtain a sample complexity of $O(dN)$. Moreover, we generalize the matrix max-norm definition to tensors, which results in a max-quasi-norm (max-qnorm) whose unit ball has small Rademacher complexity. We prove that solving a constrained least squares estimation using either the convex atomic-norm or the nonconvex max-qnorm results in optimal sample complexity for the problem of low-rank tensor completion. Furthermore, we show that these bounds are nearly minimax rate-optimal. We also provide promising numerical results for max-qnorm constrained tensor completion, showing improved recovery results compared to matricization and alternating least squares.

Average-case Hardness of RIP Certification

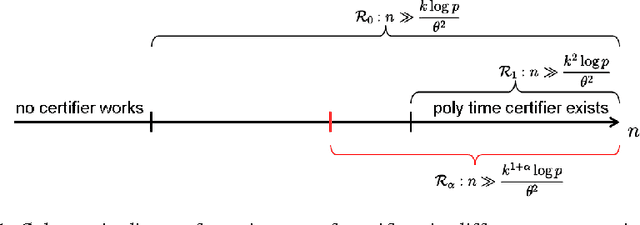
The restricted isometry property (RIP) for design matrices gives guarantees for optimal recovery in sparse linear models. It is of high interest in compressed sensing and statistical learning. This property is particularly important for computationally efficient recovery methods. As a consequence, even though it is in general NP-hard to check that RIP holds, there have been substantial efforts to find tractable proxies for it. These would allow the construction of RIP matrices and the polynomial-time verification of RIP given an arbitrary matrix. We consider the framework of average-case certifiers, that never wrongly declare that a matrix is RIP, while being often correct for random instances. While there are such functions which are tractable in a suboptimal parameter regime, we show that this is a computationally hard task in any better regime. Our results are based on a new, weaker assumption on the problem of detecting dense subgraphs.