Model-adapted Fourier sampling for generative compressed sensing

We study generative compressed sensing when the measurement matrix is randomly subsampled from a unitary matrix (with the DFT as an important special case). It was recently shown that $\textit{O}(kdn\| \boldsymbol{\alpha}\|_{\infty}^{2})$ uniformly random Fourier measurements are sufficient to recover signals in the range of a neural network $G:\mathbb{R}^k \to \mathbb{R}^n$ of depth $d$, where each component of the so-called local coherence vector $\boldsymbol{\alpha}$ quantifies the alignment of a corresponding Fourier vector with the range of $G$. We construct a model-adapted sampling strategy with an improved sample complexity of $\textit{O}(kd\| \boldsymbol{\alpha}\|_{2}^{2})$ measurements. This is enabled by: (1) new theoretical recovery guarantees that we develop for nonuniformly random sampling distributions and then (2) optimizing the sampling distribution to minimize the number of measurements needed for these guarantees. This development offers a sample complexity applicable to natural signal classes, which are often almost maximally coherent with low Fourier frequencies. Finally, we consider a surrogate sampling scheme, and validate its performance in recovery experiments using the CelebA dataset.

Square Root LASSO: Well-posedness, Lipschitz stability and the tuning trade off

This paper studies well-posedness and parameter sensitivity of the Square Root LASSO (SR-LASSO), an optimization model for recovering sparse solutions to linear inverse problems in finite dimension. An advantage of the SR-LASSO (e.g., over the standard LASSO) is that the optimal tuning of the regularization parameter is robust with respect to measurement noise. This paper provides three point-based regularity conditions at a solution of the SR-LASSO: the weak, intermediate, and strong assumptions. It is shown that the weak assumption implies uniqueness of the solution in question. The intermediate assumption yields a directionally differentiable and locally Lipschitz solution map (with explicit Lipschitz bounds), whereas the strong assumption gives continuous differentiability of said map around the point in question. Our analysis leads to new theoretical insights on the comparison between SR-LASSO and LASSO from the viewpoint of tuning parameter sensitivity: noise-robust optimal parameter choice for SR-LASSO comes at the "price" of elevated tuning parameter sensitivity. Numerical results support and showcase the theoretical findings.

Learning from few examples: Classifying sex from retinal images via deep learning

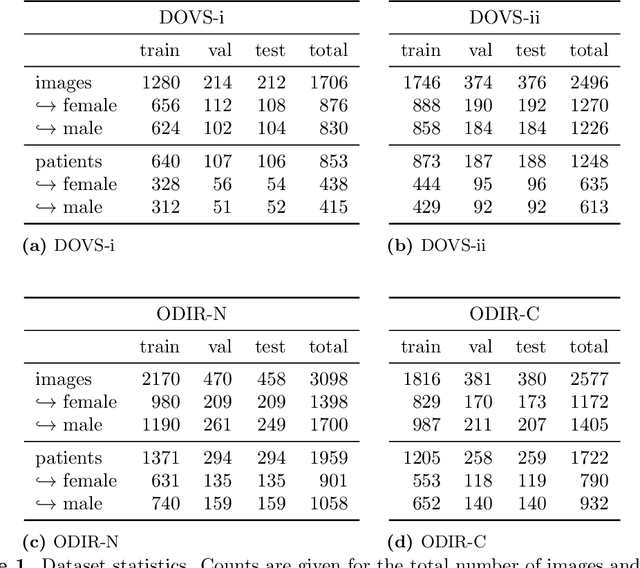
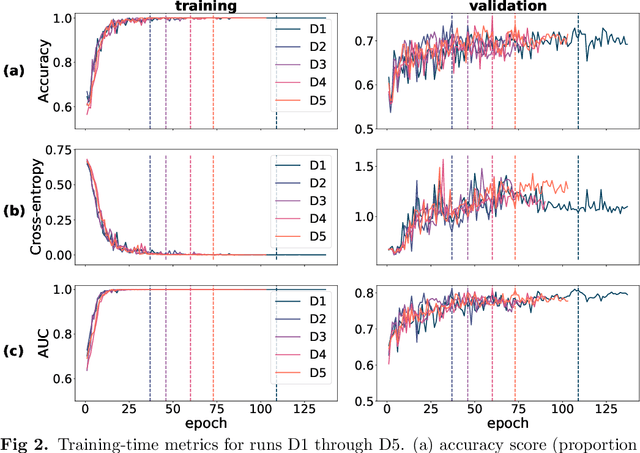
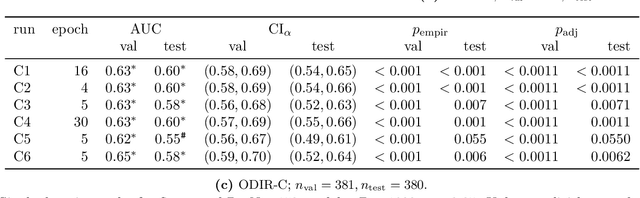
Deep learning has seen tremendous interest in medical imaging, particularly in the use of convolutional neural networks (CNNs) for developing automated diagnostic tools. The facility of its non-invasive acquisition makes retinal fundus imaging amenable to such automated approaches. Recent work in analyzing fundus images using CNNs relies on access to massive data for training and validation - hundreds of thousands of images. However, data residency and data privacy restrictions stymie the applicability of this approach in medical settings where patient confidentiality is a mandate. Here, we showcase results for the performance of DL on small datasets to classify patient sex from fundus images - a trait thought not to be present or quantifiable in fundus images until recently. We fine-tune a Resnet-152 model whose last layer has been modified for binary classification. In several experiments, we assess performance in the small dataset context using one private (DOVS) and one public (ODIR) data source. Our models, developed using approximately 2500 fundus images, achieved test AUC scores of up to 0.72 (95% CI: [0.67, 0.77]). This corresponds to a mere 25% decrease in performance despite a nearly 1000-fold decrease in the dataset size compared to prior work in the literature. Even with a hard task like sex categorization from retinal images, we find that classification is possible with very small datasets. Additionally, we perform domain adaptation experiments between DOVS and ODIR; explore the effect of data curation on training and generalizability; and investigate model ensembling to maximize CNN classifier performance in the context of small development datasets.

A coherence parameter characterizing generative compressed sensing with Fourier measurements

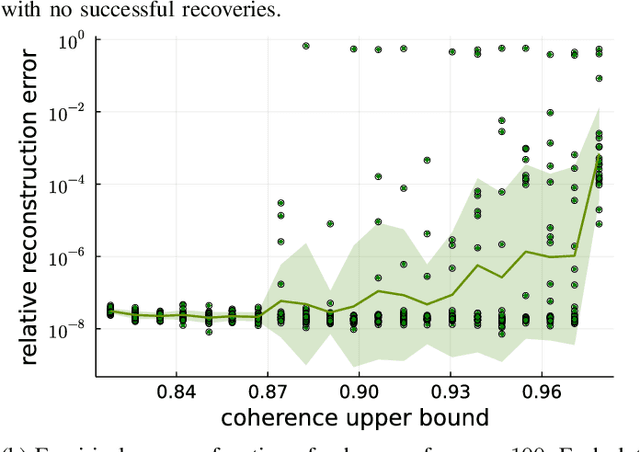
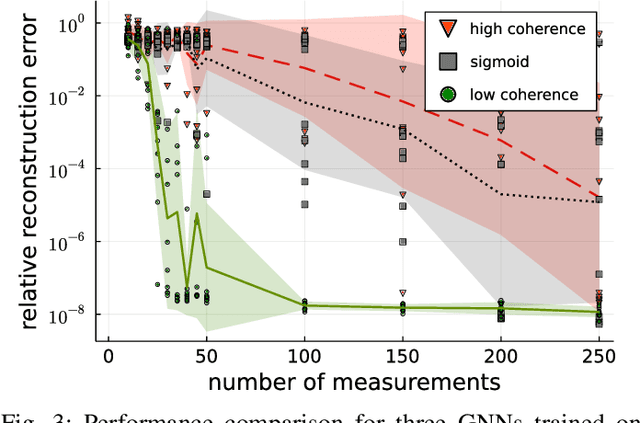
In Bora et al. (2017), a mathematical framework was developed for compressed sensing guarantees in the setting where the measurement matrix is Gaussian and the signal structure is the range of a generative neural network (GNN). The problem of compressed sensing with GNNs has since been extensively analyzed when the measurement matrix and/or network weights follow a subgaussian distribution. We move beyond the subgaussian assumption, to measurement matrices that are derived by sampling uniformly at random rows of a unitary matrix (including subsampled Fourier measurements as a special case). Specifically, we prove the first known restricted isometry guarantee for generative compressed sensing with subsampled isometries, and provide recovery bounds with nearly order-optimal sample complexity, addressing an open problem of Scarlett et al. (2022, p. 10). Recovery efficacy is characterized by the coherence, a new parameter, which measures the interplay between the range of the network and the measurement matrix. Our approach relies on subspace counting arguments and ideas central to high-dimensional probability. Furthermore, we propose a regularization strategy for training GNNs to have favourable coherence with the measurement operator. We provide compelling numerical simulations that support this regularized training strategy: our strategy yields low coherence networks that require fewer measurements for signal recovery. This, together with our theoretical results, supports coherence as a natural quantity for characterizing generative compressed sensing with subsampled isometries.

Deep generative demixing: Recovering Lipschitz signals from noisy subgaussian mixtures

Generative neural networks (GNNs) have gained renown for efficaciously capturing intrinsic low-dimensional structure in natural images. Here, we investigate the subgaussian demixing problem for two Lipschitz signals, with GNN demixing as a special case. In demixing, one seeks identification of two signals given their sum and prior structural information. Here, we assume each signal lies in the range of a Lipschitz function, which includes many popular GNNs as a special case. We prove a sample complexity bound for nearly optimal recovery error that extends a recent result of Bora, et al. (2017) from the compressed sensing setting with gaussian matrices to demixing with subgaussian ones. Under a linear signal model in which the signals lie in convex sets, McCoy & Tropp (2014) have characterized the sample complexity for identification under subgaussian mixing. In the present setting, the signal structure need not be convex. For example, our result applies to a domain that is a non-convex union of convex cones. We support the efficacy of this demixing model with numerical simulations using trained GNNs, suggesting an algorithm that would be an interesting object of further theoretical study.