Sample-Efficient Private Learning of Mixtures of Gaussians

We study the problem of learning mixtures of Gaussians with approximate differential privacy. We prove that roughly $kd^2 + k^{1.5} d^{1.75} + k^2 d$ samples suffice to learn a mixture of $k$ arbitrary $d$-dimensional Gaussians up to low total variation distance, with differential privacy. Our work improves over the previous best result [AAL24b] (which required roughly $k^2 d^4$ samples) and is provably optimal when $d$ is much larger than $k^2$. Moreover, we give the first optimal bound for privately learning mixtures of $k$ univariate (i.e., $1$-dimensional) Gaussians. Importantly, we show that the sample complexity for privately learning mixtures of univariate Gaussians is linear in the number of components $k$, whereas the previous best sample complexity [AAL21] was quadratic in $k$. Our algorithms utilize various techniques, including the inverse sensitivity mechanism [AD20b, AD20a, HKMN23], sample compression for distributions [ABDH+20], and methods for bounding volumes of sumsets.

Agnostic Private Density Estimation via Stable List Decoding

We introduce a new notion of stability--which we call stable list decoding--and demonstrate its applicability in designing differentially private density estimators. This definition is weaker than global stability [ABLMM22] and is related to the notions of replicability [ILPS22] and list replicability [CMY23]. We show that if a class of distributions is stable list decodable, then it can be learned privately in the agnostic setting. As the main application of our framework, we prove the first upper bound on the sample complexity of private density estimation for Gaussian Mixture Models in the agnostic setting, extending the realizable result of Afzali et al. [AAL24].

Sample-Optimal Locally Private Hypothesis Selection and the Provable Benefits of Interactivity

We study the problem of hypothesis selection under the constraint of local differential privacy. Given a class $\mathcal{F}$ of $k$ distributions and a set of i.i.d. samples from an unknown distribution $h$, the goal of hypothesis selection is to pick a distribution $\hat{f}$ whose total variation distance to $h$ is comparable with the best distribution in $\mathcal{F}$ (with high probability). We devise an $\varepsilon$-locally-differentially-private ($\varepsilon$-LDP) algorithm that uses $\Theta\left(\frac{k}{\alpha^2\min \{\varepsilon^2,1\}}\right)$ samples to guarantee that $d_{TV}(h,\hat{f})\leq \alpha + 9 \min_{f\in \mathcal{F}}d_{TV}(h,f)$ with high probability. This sample complexity is optimal for $\varepsilon<1$, matching the lower bound of Gopi et al. (2020). All previously known algorithms for this problem required $\Omega\left(\frac{k\log k}{\alpha^2\min \{ \varepsilon^2 ,1\}} \right)$ samples to work. Moreover, our result demonstrates the power of interaction for $\varepsilon$-LDP hypothesis selection. Namely, it breaks the known lower bound of $\Omega\left(\frac{k\log k}{\alpha^2\min \{ \varepsilon^2 ,1\}} \right)$ for the sample complexity of non-interactive hypothesis selection. Our algorithm breaks this barrier using only $\Theta(\log \log k)$ rounds of interaction. To prove our results, we define the notion of \emph{critical queries} for a Statistical Query Algorithm (SQA) which may be of independent interest. Informally, an SQA is said to use a small number of critical queries if its success relies on the accuracy of only a small number of queries it asks. We then design an LDP algorithm that uses a smaller number of critical queries.

Mixtures of Gaussians are Privately Learnable with a Polynomial Number of Samples

We study the problem of estimating mixtures of Gaussians under the constraint of differential privacy (DP). Our main result is that $\tilde{O}(k^2 d^4 \log(1/\delta) / \alpha^2 \varepsilon)$ samples are sufficient to estimate a mixture of $k$ Gaussians up to total variation distance $\alpha$ while satisfying $(\varepsilon, \delta)$-DP. This is the first finite sample complexity upper bound for the problem that does not make any structural assumptions on the GMMs. To solve the problem, we devise a new framework which may be useful for other tasks. On a high level, we show that if a class of distributions (such as Gaussians) is (1) list decodable and (2) admits a "locally small'' cover [BKSW19] with respect to total variation distance, then the class of its mixtures is privately learnable. The proof circumvents a known barrier indicating that, unlike Gaussians, GMMs do not admit a locally small cover [AAL21].

On the Role of Noise in the Sample Complexity of Learning Recurrent Neural Networks: Exponential Gaps for Long Sequences

We consider the class of noisy multi-layered sigmoid recurrent neural networks with $w$ (unbounded) weights for classification of sequences of length $T$, where independent noise distributed according to $\mathcal{N}(0,\sigma^2)$ is added to the output of each neuron in the network. Our main result shows that the sample complexity of PAC learning this class can be bounded by $O (w\log(T/\sigma))$. For the non-noisy version of the same class (i.e., $\sigma=0$), we prove a lower bound of $\Omega (wT)$ for the sample complexity. Our results indicate an exponential gap in the dependence of sample complexity on $T$ for noisy versus non-noisy networks. Moreover, given the mild logarithmic dependence of the upper bound on $1/\sigma$, this gap still holds even for numerically negligible values of $\sigma$.

Polynomial Time and Private Learning of Unbounded Gaussian Mixture Models

We study the problem of privately estimating the parameters of $d$-dimensional Gaussian Mixture Models (GMMs) with $k$ components. For this, we develop a technique to reduce the problem to its non-private counterpart. This allows us to privatize existing non-private algorithms in a blackbox manner, while incurring only a small overhead in the sample complexity and running time. As the main application of our framework, we develop an $(\varepsilon, \delta)$-differentially private algorithm to learn GMMs using the non-private algorithm of Moitra and Valiant [MV10] as a blackbox. Consequently, this gives the first sample complexity upper bound and first polynomial time algorithm for privately learning GMMs without any boundedness assumptions on the parameters.

Benefits of Additive Noise in Composing Classes with Bounded Capacity

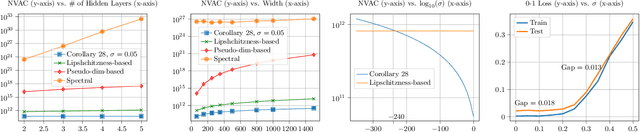
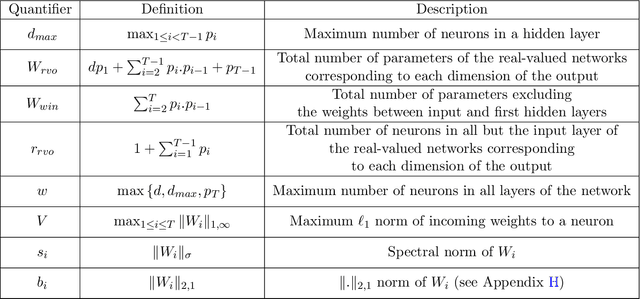
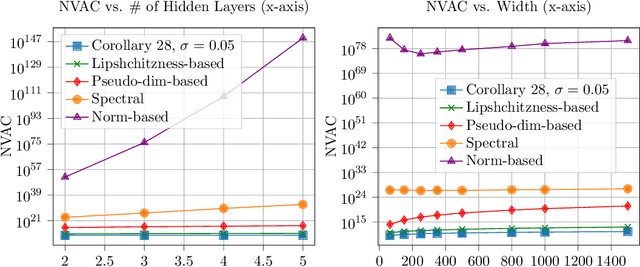
We observe that given two (compatible) classes of functions $\mathcal{F}$ and $\mathcal{H}$ with small capacity as measured by their uniform covering numbers, the capacity of the composition class $\mathcal{H} \circ \mathcal{F}$ can become prohibitively large or even unbounded. We then show that adding a small amount of Gaussian noise to the output of $\mathcal{F}$ before composing it with $\mathcal{H}$ can effectively control the capacity of $\mathcal{H} \circ \mathcal{F}$, offering a general recipe for modular design. To prove our results, we define new notions of uniform covering number of random functions with respect to the total variation and Wasserstein distances. We instantiate our results for the case of multi-layer sigmoid neural networks. Preliminary empirical results on MNIST dataset indicate that the amount of noise required to improve over existing uniform bounds can be numerically negligible (i.e., element-wise i.i.d. Gaussian noise with standard deviation $10^{-240}$). The source codes are available at https://github.com/fathollahpour/composition_noise.

Adversarially Robust Learning with Tolerance

We study the problem of tolerant adversarial PAC learning with respect to metric perturbation sets. In adversarial PAC learning, an adversary is allowed to replace a test point $x$ with an arbitrary point in a closed ball of radius $r$ centered at $x$. In the tolerant version, the error of the learner is compared with the best achievable error with respect to a slightly larger perturbation radius $(1+\gamma)r$. For perturbation sets with doubling dimension $d$, we show that a variant of the natural ``perturb-and-smooth'' algorithm PAC learns any hypothesis class $\mathcal{H}$ with VC dimension $v$ in the $\gamma$-tolerant adversarial setting with $O\left(\frac{v(1+1/\gamma)^{O(d)}}{\varepsilon}\right)$ samples. This is the first such general guarantee with linear dependence on $v$ even for the special case where the domain is the real line and the perturbation sets are closed balls (intervals) of radius $r$. However, the proposed guarantees for the perturb-and-smooth algorithm currently only hold in the tolerant robust realizable setting and exhibit exponential dependence on $d$. We additionally propose an alternative learning method which yields sample complexity bounds with only linear dependence on the doubling dimension even in the more general agnostic case. This approach is based on sample compression.

Private and polynomial time algorithms for learning Gaussians and beyond

We present a fairly general framework for reducing $(\varepsilon, \delta)$ differentially private (DP) statistical estimation to its non-private counterpart. As the main application of this framework, we give a polynomial time and $(\varepsilon,\delta)$-DP algorithm for learning (unrestricted) Gaussian distributions in $\mathbb{R}^d$. The sample complexity of our approach for learning the Gaussian up to total variation distance $\alpha$ is $\widetilde{O}\left(\frac{d^2}{\alpha^2}+\frac{d^2 \sqrt{\ln{1/\delta}}}{\alpha\varepsilon} \right)$, matching (up to logarithmic factors) the best known information-theoretic (non-efficient) sample complexity upper bound of Aden-Ali, Ashtiani, Kamath~(ALT'21). In an independent work, Kamath, Mouzakis, Singhal, Steinke, and Ullman~(arXiv:2111.04609) proved a similar result using a different approach and with $O(d^{5/2})$ sample complexity dependence on $d$. As another application of our framework, we provide the first polynomial time $(\varepsilon, \delta)$-DP algorithm for robust learning of (unrestricted) Gaussians.

Privately Learning Mixtures of Axis-Aligned Gaussians

We consider the problem of learning mixtures of Gaussians under the constraint of approximate differential privacy. We prove that $\widetilde{O}(k^2 d \log^{3/2}(1/\delta) / \alpha^2 \varepsilon)$ samples are sufficient to learn a mixture of $k$ axis-aligned Gaussians in $\mathbb{R}^d$ to within total variation distance $\alpha$ while satisfying $(\varepsilon, \delta)$-differential privacy. This is the first result for privately learning mixtures of unbounded axis-aligned (or even unbounded univariate) Gaussians. If the covariance matrices of each of the Gaussians is the identity matrix, we show that $\widetilde{O}(kd/\alpha^2 + kd \log(1/\delta) / \alpha \varepsilon)$ samples are sufficient. Recently, the "local covering" technique of Bun, Kamath, Steinke, and Wu has been successfully used for privately learning high-dimensional Gaussians with a known covariance matrix and extended to privately learning general high-dimensional Gaussians by Aden-Ali, Ashtiani, and Kamath. Given these positive results, this approach has been proposed as a promising direction for privately learning mixtures of Gaussians. Unfortunately, we show that this is not possible. We design a new technique for privately learning mixture distributions. A class of distributions $\mathcal{F}$ is said to be list-decodable if there is an algorithm that, given "heavily corrupted" samples from $f\in \mathcal{F}$, outputs a list of distributions, $\widehat{\mathcal{F}}$, such that one of the distributions in $\widehat{\mathcal{F}}$ approximates $f$. We show that if $\mathcal{F}$ is privately list-decodable, then we can privately learn mixtures of distributions in $\mathcal{F}$. Finally, we show axis-aligned Gaussian distributions are privately list-decodable, thereby proving mixtures of such distributions are privately learnable.