Optimal anytime regret with two experts

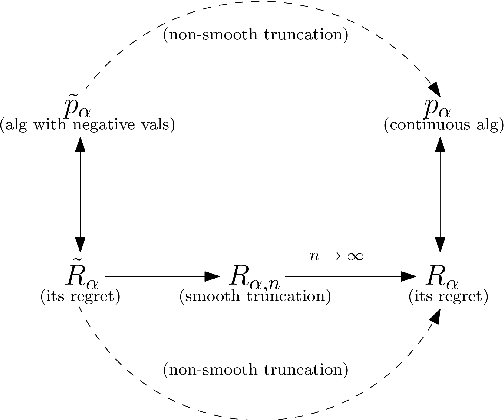
The multiplicative weights method is an algorithm for the problem of prediction with expert advice. It achieves the minimax regret asymptotically if the number of experts is large, and the time horizon is known in advance. Optimal algorithms are also known if there are exactly two or three experts, and the time horizon is known in advance. In the anytime setting, where the time horizon is not known in advance, algorithms can be obtained by the doubling trick, but they are not optimal, let alone practical. No minimax optimal algorithm was previously known in the anytime setting, regardless of the number of experts. We design the first minimax optimal algorithm for minimizing regret in the anytime setting. We consider the case of two experts, and prove that the optimal regret is $\gamma \sqrt{t} / 2$ at all time steps $t$, where $\gamma$ is a natural constant that arose 35 years ago in studying fundamental properties of Brownian motion. The algorithm is designed by considering a continuous analogue, which is solved using ideas from stochastic calculus.

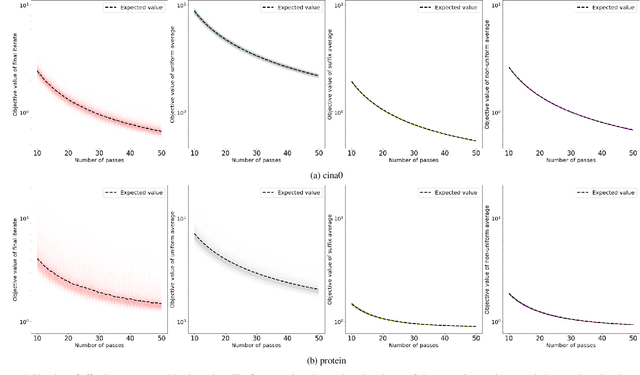
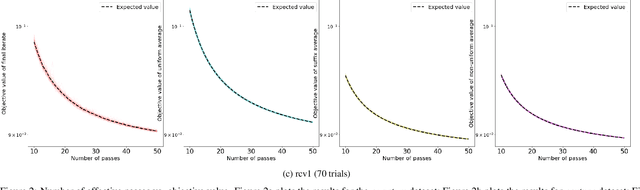
Simple and optimal high-probability bounds for strongly-convex stochastic gradient descent

We consider stochastic gradient descent algorithms for minimizing a non-smooth, strongly-convex function. Several forms of this algorithm, including suffix averaging, are known to achieve the optimal $O(1/T)$ convergence rate in expectation. We consider a simple, non-uniform averaging strategy of Lacoste-Julien et al. (2011) and prove that it achieves the optimal $O(1/T)$ convergence rate with high probability. Our proof uses a recently developed generalization of Freedman's inequality. Finally, we compare several of these algorithms experimentally and show that this non-uniform averaging strategy outperforms many standard techniques, and with smaller variance.

Tight Analyses for Non-Smooth Stochastic Gradient Descent

Consider the problem of minimizing functions that are Lipschitz and strongly convex, but not necessarily differentiable. We prove that after $T$ steps of stochastic gradient descent, the error of the final iterate is $O(\log(T)/T)$ with high probability. We also construct a function from this class for which the error of the final iterate of deterministic gradient descent is $\Omega(\log(T)/T)$. This shows that the upper bound is tight and that, in this setting, the last iterate of stochastic gradient descent has the same general error rate (with high probability) as deterministic gradient descent. This resolves both open questions posed by Shamir (2012). An intermediate step of our analysis proves that the suffix averaging method achieves error $O(1/T)$ with high probability, which is optimal (for any first-order optimization method). This improves results of Rakhlin (2012) and Hazan and Kale (2014), both of which achieved error $O(1/T)$, but only in expectation, and achieved a high probability error bound of $O(\log \log(T)/T)$, which is suboptimal. We prove analogous results for functions that are Lipschitz and convex, but not necessarily strongly convex or differentiable. After $T$ steps of stochastic gradient descent, the error of the final iterate is $O(\log(T)/\sqrt{T})$ with high probability, and there exists a function for which the error of the final iterate of deterministic gradient descent is $\Omega(\log(T)/\sqrt{T})$.