Agnostic Private Density Estimation via Stable List Decoding

We introduce a new notion of stability--which we call stable list decoding--and demonstrate its applicability in designing differentially private density estimators. This definition is weaker than global stability [ABLMM22] and is related to the notions of replicability [ILPS22] and list replicability [CMY23]. We show that if a class of distributions is stable list decodable, then it can be learned privately in the agnostic setting. As the main application of our framework, we prove the first upper bound on the sample complexity of private density estimation for Gaussian Mixture Models in the agnostic setting, extending the realizable result of Afzali et al. [AAL24].

Improved Online Learning Algorithms for CTR Prediction in Ad Auctions

In this work, we investigate the online learning problem of revenue maximization in ad auctions, where the seller needs to learn the click-through rates (CTRs) of each ad candidate and charge the price of the winner through a pay-per-click manner. We focus on two models of the advertisers' strategic behaviors. First, we assume that the advertiser is completely myopic; i.e.~in each round, they aim to maximize their utility only for the current round. In this setting, we develop an online mechanism based on upper-confidence bounds that achieves a tight $O(\sqrt{T})$ regret in the worst-case and negative regret when the values are static across all the auctions and there is a gap between the highest expected value (i.e.~value multiplied by their CTR) and second highest expected value ad. Next, we assume that the advertiser is non-myopic and cares about their long term utility. This setting is much more complex since an advertiser is incentivized to influence the mechanism by bidding strategically in earlier rounds. In this setting, we provide an algorithm to achieve negative regret for the static valuation setting (with a positive gap), which is in sharp contrast with the prior work that shows $O(T^{2/3})$ regret when the valuation is generated by adversary.

Mixtures of Gaussians are Privately Learnable with a Polynomial Number of Samples

We study the problem of estimating mixtures of Gaussians under the constraint of differential privacy (DP). Our main result is that $\tilde{O}(k^2 d^4 \log(1/\delta) / \alpha^2 \varepsilon)$ samples are sufficient to estimate a mixture of $k$ Gaussians up to total variation distance $\alpha$ while satisfying $(\varepsilon, \delta)$-DP. This is the first finite sample complexity upper bound for the problem that does not make any structural assumptions on the GMMs. To solve the problem, we devise a new framework which may be useful for other tasks. On a high level, we show that if a class of distributions (such as Gaussians) is (1) list decodable and (2) admits a "locally small'' cover [BKSW19] with respect to total variation distance, then the class of its mixtures is privately learnable. The proof circumvents a known barrier indicating that, unlike Gaussians, GMMs do not admit a locally small cover [AAL21].

Polynomial Time and Private Learning of Unbounded Gaussian Mixture Models

We study the problem of privately estimating the parameters of $d$-dimensional Gaussian Mixture Models (GMMs) with $k$ components. For this, we develop a technique to reduce the problem to its non-private counterpart. This allows us to privatize existing non-private algorithms in a blackbox manner, while incurring only a small overhead in the sample complexity and running time. As the main application of our framework, we develop an $(\varepsilon, \delta)$-differentially private algorithm to learn GMMs using the non-private algorithm of Moitra and Valiant [MV10] as a blackbox. Consequently, this gives the first sample complexity upper bound and first polynomial time algorithm for privately learning GMMs without any boundedness assumptions on the parameters.

User Response in Ad Auctions: An MDP Formulation of Long-Term Revenue Optimization

We propose a new Markov Decision Process (MDP) model for ad auctions to capture the user response to the quality of ads, with the objective of maximizing the long-term discounted revenue. By incorporating user response, our model takes into consideration all three parties involved in the auction (advertiser, auctioneer, and user). The state of the user is modeled as a user-specific click-through rate (CTR) with the CTR changing in the next round according to the set of ads shown to the user in the current round. We characterize the optimal mechanism for this MDP as a Myerson's auction with a notion of modified virtual value, which relies on the value distribution of the advertiser, the current user state, and the future impact of showing the ad to the user. Moreover, we propose a simple mechanism built upon second price auctions with personalized reserve prices and show it can achieve a constant-factor approximation to the optimal long term discounted revenue.

Continuous Prediction with Experts' Advice

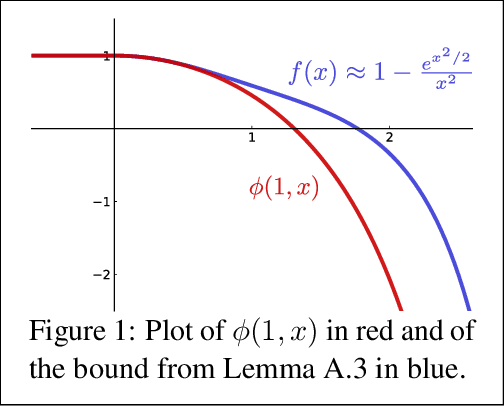
Prediction with experts' advice is one of the most fundamental problems in online learning and captures many of its technical challenges. A recent line of work has looked at online learning through the lens of differential equations and continuous-time analysis. This viewpoint has yielded optimal results for several problems in online learning. In this paper, we employ continuous-time stochastic calculus in order to study the discrete-time experts' problem. We use these tools to design a continuous-time, parameter-free algorithm with improved guarantees for the quantile regret. We then develop an analogous discrete-time algorithm with a very similar analysis and identical quantile regret bounds. Finally, we design an anytime continuous-time algorithm with regret matching the optimal fixed-time rate when the gains are independent Brownian Motions; in many settings, this is the most difficult case. This gives some evidence that, even with adversarial gains, the optimal anytime and fixed-time regrets may coincide.

Private and polynomial time algorithms for learning Gaussians and beyond

We present a fairly general framework for reducing $(\varepsilon, \delta)$ differentially private (DP) statistical estimation to its non-private counterpart. As the main application of this framework, we give a polynomial time and $(\varepsilon,\delta)$-DP algorithm for learning (unrestricted) Gaussian distributions in $\mathbb{R}^d$. The sample complexity of our approach for learning the Gaussian up to total variation distance $\alpha$ is $\widetilde{O}\left(\frac{d^2}{\alpha^2}+\frac{d^2 \sqrt{\ln{1/\delta}}}{\alpha\varepsilon} \right)$, matching (up to logarithmic factors) the best known information-theoretic (non-efficient) sample complexity upper bound of Aden-Ali, Ashtiani, Kamath~(ALT'21). In an independent work, Kamath, Mouzakis, Singhal, Steinke, and Ullman~(arXiv:2111.04609) proved a similar result using a different approach and with $O(d^{5/2})$ sample complexity dependence on $d$. As another application of our framework, we provide the first polynomial time $(\varepsilon, \delta)$-DP algorithm for robust learning of (unrestricted) Gaussians.

Privately Learning Mixtures of Axis-Aligned Gaussians

We consider the problem of learning mixtures of Gaussians under the constraint of approximate differential privacy. We prove that $\widetilde{O}(k^2 d \log^{3/2}(1/\delta) / \alpha^2 \varepsilon)$ samples are sufficient to learn a mixture of $k$ axis-aligned Gaussians in $\mathbb{R}^d$ to within total variation distance $\alpha$ while satisfying $(\varepsilon, \delta)$-differential privacy. This is the first result for privately learning mixtures of unbounded axis-aligned (or even unbounded univariate) Gaussians. If the covariance matrices of each of the Gaussians is the identity matrix, we show that $\widetilde{O}(kd/\alpha^2 + kd \log(1/\delta) / \alpha \varepsilon)$ samples are sufficient. Recently, the "local covering" technique of Bun, Kamath, Steinke, and Wu has been successfully used for privately learning high-dimensional Gaussians with a known covariance matrix and extended to privately learning general high-dimensional Gaussians by Aden-Ali, Ashtiani, and Kamath. Given these positive results, this approach has been proposed as a promising direction for privately learning mixtures of Gaussians. Unfortunately, we show that this is not possible. We design a new technique for privately learning mixture distributions. A class of distributions $\mathcal{F}$ is said to be list-decodable if there is an algorithm that, given "heavily corrupted" samples from $f\in \mathcal{F}$, outputs a list of distributions, $\widehat{\mathcal{F}}$, such that one of the distributions in $\widehat{\mathcal{F}}$ approximates $f$. We show that if $\mathcal{F}$ is privately list-decodable, then we can privately learn mixtures of distributions in $\mathcal{F}$. Finally, we show axis-aligned Gaussian distributions are privately list-decodable, thereby proving mixtures of such distributions are privately learnable.

Optimal anytime regret with two experts

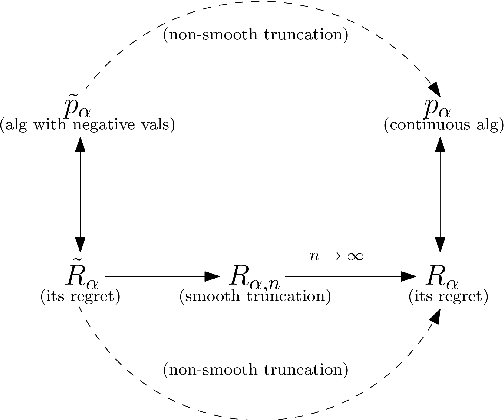
The multiplicative weights method is an algorithm for the problem of prediction with expert advice. It achieves the minimax regret asymptotically if the number of experts is large, and the time horizon is known in advance. Optimal algorithms are also known if there are exactly two or three experts, and the time horizon is known in advance. In the anytime setting, where the time horizon is not known in advance, algorithms can be obtained by the doubling trick, but they are not optimal, let alone practical. No minimax optimal algorithm was previously known in the anytime setting, regardless of the number of experts. We design the first minimax optimal algorithm for minimizing regret in the anytime setting. We consider the case of two experts, and prove that the optimal regret is $\gamma \sqrt{t} / 2$ at all time steps $t$, where $\gamma$ is a natural constant that arose 35 years ago in studying fundamental properties of Brownian motion. The algorithm is designed by considering a continuous analogue, which is solved using ideas from stochastic calculus.

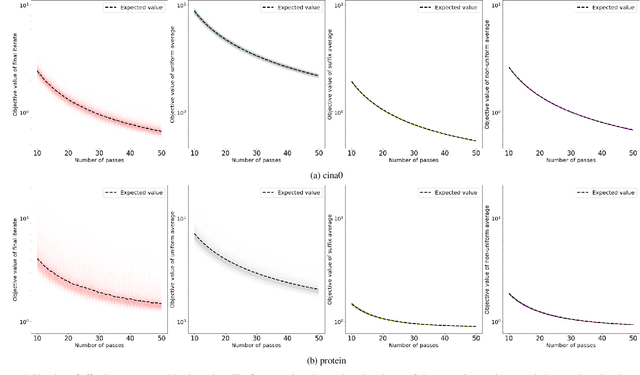
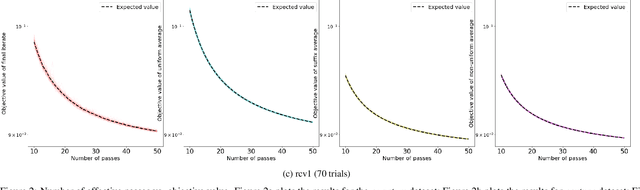
Simple and optimal high-probability bounds for strongly-convex stochastic gradient descent

We consider stochastic gradient descent algorithms for minimizing a non-smooth, strongly-convex function. Several forms of this algorithm, including suffix averaging, are known to achieve the optimal $O(1/T)$ convergence rate in expectation. We consider a simple, non-uniform averaging strategy of Lacoste-Julien et al. (2011) and prove that it achieves the optimal $O(1/T)$ convergence rate with high probability. Our proof uses a recently developed generalization of Freedman's inequality. Finally, we compare several of these algorithms experimentally and show that this non-uniform averaging strategy outperforms many standard techniques, and with smaller variance.