Physics-informed deep learning and compressive collocation for high-dimensional diffusion-reaction equations: practical existence theory and numerics

On the forefront of scientific computing, Deep Learning (DL), i.e., machine learning with Deep Neural Networks (DNNs), has emerged a powerful new tool for solving Partial Differential Equations (PDEs). It has been observed that DNNs are particularly well suited to weakening the effect of the curse of dimensionality, a term coined by Richard E. Bellman in the late `50s to describe challenges such as the exponential dependence of the sample complexity, i.e., the number of samples required to solve an approximation problem, on the dimension of the ambient space. However, although DNNs have been used to solve PDEs since the `90s, the literature underpinning their mathematical efficiency in terms of numerical analysis (i.e., stability, accuracy, and sample complexity), is only recently beginning to emerge. In this paper, we leverage recent advancements in function approximation using sparsity-based techniques and random sampling to develop and analyze an efficient high-dimensional PDE solver based on DL. We show, both theoretically and numerically, that it can compete with a novel stable and accurate compressive spectral collocation method. In particular, we demonstrate a new practical existence theorem, which establishes the existence of a class of trainable DNNs with suitable bounds on the network architecture and a sufficient condition on the sample complexity, with logarithmic or, at worst, linear scaling in dimension, such that the resulting networks stably and accurately approximate a diffusion-reaction PDE with high probability.

Real-Time Motion Detection Using Dynamic Mode Decomposition

Dynamic Mode Decomposition (DMD) is a numerical method that seeks to fit timeseries data to a linear dynamical system. In doing so, DMD decomposes dynamic data into spatially coherent modes that evolve in time according to exponential growth/decay or with a fixed frequency of oscillation. A prolific application of DMD has been to video, where one interprets the high-dimensional pixel space evolving through time as the video plays. In this work, we propose a simple and interpretable motion detection algorithm for streaming video data rooted in DMD. Our method leverages the fact that there exists a correspondence between the evolution of important video features, such as foreground motion, and the eigenvalues of the matrix which results from applying DMD to segments of video. We apply the method to a database of test videos which emulate security footage under varying realistic conditions. Effectiveness is analyzed using receiver operating characteristic curves, while we use cross-validation to optimize the threshold parameter that identifies movement.

Learning smooth functions in high dimensions: from sparse polynomials to deep neural networks

Learning approximations to smooth target functions of many variables from finite sets of pointwise samples is an important task in scientific computing and its many applications in computational science and engineering. Despite well over half a century of research on high-dimensional approximation, this remains a challenging problem. Yet, significant advances have been made in the last decade towards efficient methods for doing this, commencing with so-called sparse polynomial approximation methods and continuing most recently with methods based on Deep Neural Networks (DNNs). In tandem, there have been substantial advances in the relevant approximation theory and analysis of these techniques. In this work, we survey this recent progress. We describe the contemporary motivations for this problem, which stem from parametric models and computational uncertainty quantification; the relevant function classes, namely, classes of infinite-dimensional, Banach-valued, holomorphic functions; fundamental limits of learnability from finite data for these classes; and finally, sparse polynomial and DNN methods for efficiently learning such functions from finite data. For the latter, there is currently a significant gap between the approximation theory of DNNs and the practical performance of deep learning. Aiming to narrow this gap, we develop the topic of practical existence theory, which asserts the existence of dimension-independent DNN architectures and training strategies that achieve provably near-optimal generalization errors in terms of the amount of training data.

Neural Rank Collapse: Weight Decay and Small Within-Class Variability Yield Low-Rank Bias

Recent work in deep learning has shown strong empirical and theoretical evidence of an implicit low-rank bias: weight matrices in deep networks tend to be approximately low-rank and removing relatively small singular values during training or from available trained models may significantly reduce model size while maintaining or even improving model performance. However, the majority of the theoretical investigations around low-rank bias in neural networks deal with oversimplified deep linear networks. In this work, we consider general networks with nonlinear activations and the weight decay parameter, and we show the presence of an intriguing neural rank collapse phenomenon, connecting the low-rank bias of trained networks with networks' neural collapse properties: as the weight decay parameter grows, the rank of each layer in the network decreases proportionally to the within-class variability of the hidden-space embeddings of the previous layers. Our theoretical findings are supported by a range of experimental evaluations illustrating the phenomenon.

A practical existence theorem for reduced order models based on convolutional autoencoders

In recent years, deep learning has gained increasing popularity in the fields of Partial Differential Equations (PDEs) and Reduced Order Modeling (ROM), providing domain practitioners with new powerful data-driven techniques such as Physics-Informed Neural Networks (PINNs), Neural Operators, Deep Operator Networks (DeepONets) and Deep-Learning based ROMs (DL-ROMs). In this context, deep autoencoders based on Convolutional Neural Networks (CNNs) have proven extremely effective, outperforming established techniques, such as the reduced basis method, when dealing with complex nonlinear problems. However, despite the empirical success of CNN-based autoencoders, there are only a few theoretical results supporting these architectures, usually stated in the form of universal approximation theorems. In particular, although the existing literature provides users with guidelines for designing convolutional autoencoders, the subsequent challenge of learning the latent features has been barely investigated. Furthermore, many practical questions remain unanswered, e.g., the number of snapshots needed for convergence or the neural network training strategy. In this work, using recent techniques from sparse high-dimensional function approximation, we fill some of these gaps by providing a new practical existence theorem for CNN-based autoencoders when the parameter-to-solution map is holomorphic. This regularity assumption arises in many relevant classes of parametric PDEs, such as the parametric diffusion equation, for which we discuss an explicit application of our general theory.

Model-adapted Fourier sampling for generative compressed sensing

We study generative compressed sensing when the measurement matrix is randomly subsampled from a unitary matrix (with the DFT as an important special case). It was recently shown that $\textit{O}(kdn\| \boldsymbol{\alpha}\|_{\infty}^{2})$ uniformly random Fourier measurements are sufficient to recover signals in the range of a neural network $G:\mathbb{R}^k \to \mathbb{R}^n$ of depth $d$, where each component of the so-called local coherence vector $\boldsymbol{\alpha}$ quantifies the alignment of a corresponding Fourier vector with the range of $G$. We construct a model-adapted sampling strategy with an improved sample complexity of $\textit{O}(kd\| \boldsymbol{\alpha}\|_{2}^{2})$ measurements. This is enabled by: (1) new theoretical recovery guarantees that we develop for nonuniformly random sampling distributions and then (2) optimizing the sampling distribution to minimize the number of measurements needed for these guarantees. This development offers a sample complexity applicable to natural signal classes, which are often almost maximally coherent with low Fourier frequencies. Finally, we consider a surrogate sampling scheme, and validate its performance in recovery experiments using the CelebA dataset.

Generalization Limits of Graph Neural Networks in Identity Effects Learning

Graph Neural Networks (GNNs) have emerged as a powerful tool for data-driven learning on various graph domains. They are usually based on a message-passing mechanism and have gained increasing popularity for their intuitive formulation, which is closely linked to the Weisfeiler-Lehman (WL) test for graph isomorphism to which they have been proven equivalent in terms of expressive power. In this work, we establish new generalization properties and fundamental limits of GNNs in the context of learning so-called identity effects, i.e., the task of determining whether an object is composed of two identical components or not. Our study is motivated by the need to understand the capabilities of GNNs when performing simple cognitive tasks, with potential applications in computational linguistics and chemistry. We analyze two case studies: (i) two-letters words, for which we show that GNNs trained via stochastic gradient descent are unable to generalize to unseen letters when utilizing orthogonal encodings like one-hot representations; (ii) dicyclic graphs, i.e., graphs composed of two cycles, for which we present positive existence results leveraging the connection between GNNs and the WL test. Our theoretical analysis is supported by an extensive numerical study.

Square Root LASSO: Well-posedness, Lipschitz stability and the tuning trade off

This paper studies well-posedness and parameter sensitivity of the Square Root LASSO (SR-LASSO), an optimization model for recovering sparse solutions to linear inverse problems in finite dimension. An advantage of the SR-LASSO (e.g., over the standard LASSO) is that the optimal tuning of the regularization parameter is robust with respect to measurement noise. This paper provides three point-based regularity conditions at a solution of the SR-LASSO: the weak, intermediate, and strong assumptions. It is shown that the weak assumption implies uniqueness of the solution in question. The intermediate assumption yields a directionally differentiable and locally Lipschitz solution map (with explicit Lipschitz bounds), whereas the strong assumption gives continuous differentiability of said map around the point in question. Our analysis leads to new theoretical insights on the comparison between SR-LASSO and LASSO from the viewpoint of tuning parameter sensitivity: noise-robust optimal parameter choice for SR-LASSO comes at the "price" of elevated tuning parameter sensitivity. Numerical results support and showcase the theoretical findings.

Is Monte Carlo a bad sampling strategy for learning smooth functions in high dimensions?

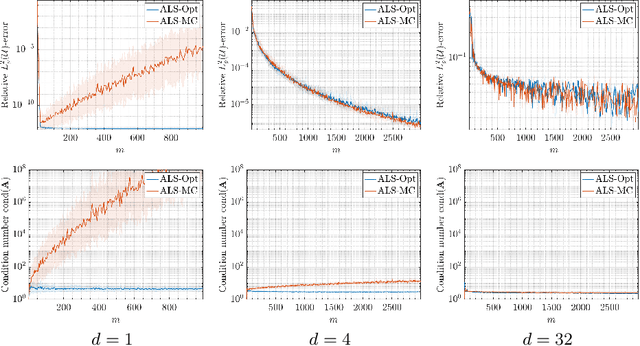
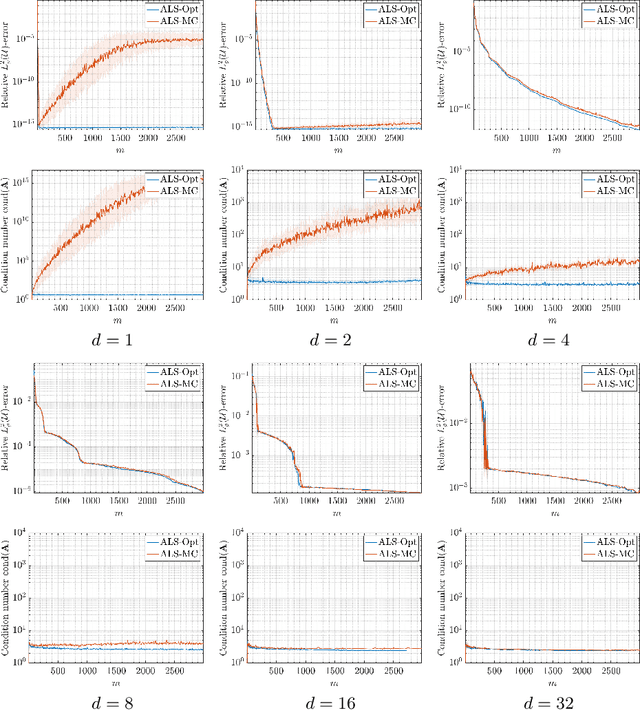
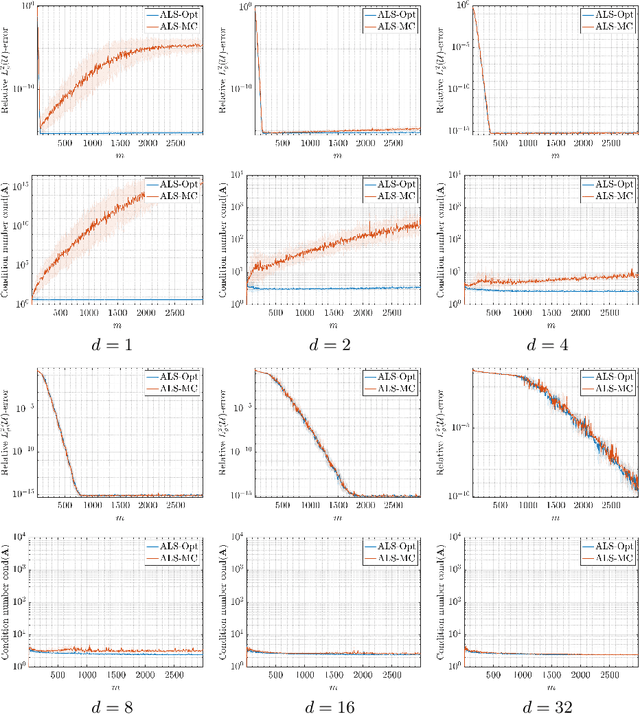
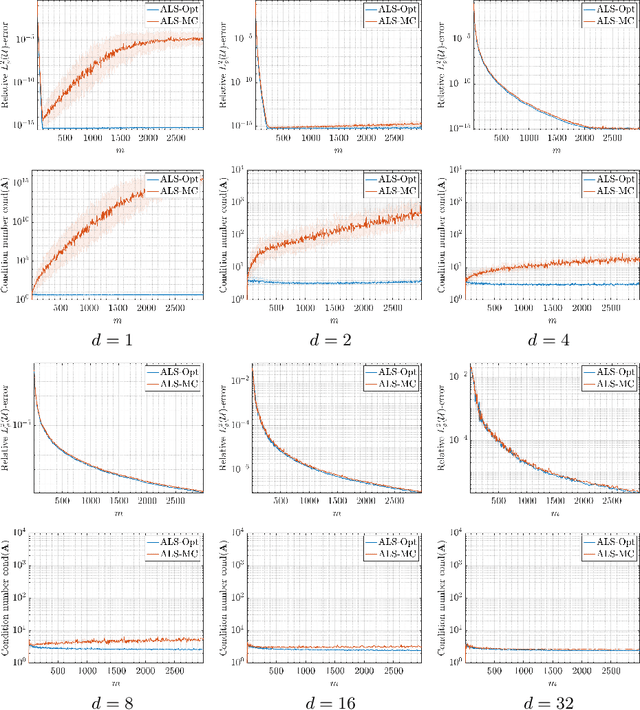
This paper concerns the approximation of smooth, high-dimensional functions from limited samples using polynomials. This task lies at the heart of many applications in computational science and engineering -- notably, those arising from parametric modelling and uncertainty quantification. It is common to use Monte Carlo (MC) sampling in such applications, so as not to succumb to the curse of dimensionality. However, it is well known this strategy is theoretically suboptimal. There are many polynomial spaces of dimension $n$ for which the sample complexity scales log-quadratically in $n$. This well-documented phenomenon has led to a concerted effort to design improved, in fact, near-optimal strategies, whose sample complexities scale log-linearly, or even linearly in $n$. Paradoxically, in this work we show that MC is actually a perfectly good strategy in high dimensions. We first document this phenomenon via several numerical examples. Next, we present a theoretical analysis that resolves this paradox for holomorphic functions of infinitely-many variables. We show that there is a least-squares scheme based on $m$ MC samples whose error decays algebraically fast in $m/\log(m)$, with a rate that is the same as that of the best $n$-term polynomial approximation. This result is non-constructive, since it assumes knowledge of a suitable polynomial space in which to perform the approximation. We next present a compressed sensing-based scheme that achieves the same rate, except for a larger polylogarithmic factor. This scheme is practical, and numerically it performs as well as or better than well-known adaptive least-squares schemes. Overall, our findings demonstrate that MC sampling is eminently suitable for smooth function approximation when the dimension is sufficiently high. Hence the benefits of improved sampling strategies are generically limited to lower-dimensional settings.

A coherence parameter characterizing generative compressed sensing with Fourier measurements

In Bora et al. (2017), a mathematical framework was developed for compressed sensing guarantees in the setting where the measurement matrix is Gaussian and the signal structure is the range of a generative neural network (GNN). The problem of compressed sensing with GNNs has since been extensively analyzed when the measurement matrix and/or network weights follow a subgaussian distribution. We move beyond the subgaussian assumption, to measurement matrices that are derived by sampling uniformly at random rows of a unitary matrix (including subsampled Fourier measurements as a special case). Specifically, we prove the first known restricted isometry guarantee for generative compressed sensing with subsampled isometries, and provide recovery bounds with nearly order-optimal sample complexity, addressing an open problem of Scarlett et al. (2022, p. 10). Recovery efficacy is characterized by the coherence, a new parameter, which measures the interplay between the range of the network and the measurement matrix. Our approach relies on subspace counting arguments and ideas central to high-dimensional probability. Furthermore, we propose a regularization strategy for training GNNs to have favourable coherence with the measurement operator. We provide compelling numerical simulations that support this regularized training strategy: our strategy yields low coherence networks that require fewer measurements for signal recovery. This, together with our theoretical results, supports coherence as a natural quantity for characterizing generative compressed sensing with subsampled isometries.