Contextual Linear Optimization with Bandit Feedback

Contextual linear optimization (CLO) uses predictive observations to reduce uncertainty in random cost coefficients and thereby improve average-cost performance. An example is a stochastic shortest path with random edge costs (e.g., traffic) and predictive features (e.g., lagged traffic, weather). Existing work on CLO assumes the data has fully observed cost coefficient vectors, but in many applications, we can only see the realized cost of a historical decision, that is, just one projection of the random cost coefficient vector, to which we refer as bandit feedback. We study a class of algorithms for CLO with bandit feedback, which we term induced empirical risk minimization (IERM), where we fit a predictive model to directly optimize the downstream performance of the policy it induces. We show a fast-rate regret bound for IERM that allows for misspecified model classes and flexible choices of the optimization estimate, and we develop computationally tractable surrogate losses. A byproduct of our theory of independent interest is fast-rate regret bound for IERM with full feedback and misspecified policy class. We compare the performance of different modeling choices numerically using a stochastic shortest path example and provide practical insights from the empirical results.

Practical Policy Optimization with Personalized Experimentation

Many organizations measure treatment effects via an experimentation platform to evaluate the casual effect of product variations prior to full-scale deployment. However, standard experimentation platforms do not perform optimally for end user populations that exhibit heterogeneous treatment effects (HTEs). Here we present a personalized experimentation framework, Personalized Experiments (PEX), which optimizes treatment group assignment at the user level via HTE modeling and sequential decision policy optimization to optimize multiple short-term and long-term outcomes simultaneously. We describe an end-to-end workflow that has proven to be successful in practice and can be readily implemented using open-source software.

Fast Rates for the Regret of Offline Reinforcement Learning

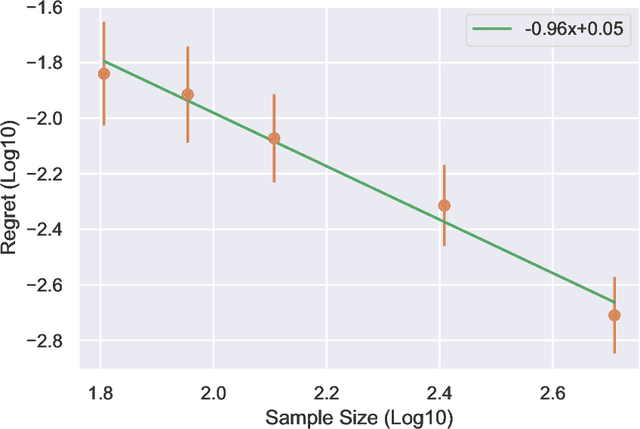
We study the regret of reinforcement learning from offline data generated by a fixed behavior policy in an infinite-horizon discounted Markov decision process (MDP). While existing analyses of common approaches, such as fitted $Q$-iteration (FQI), suggest a $O(1/\sqrt{n})$ convergence for regret, empirical behavior exhibits much faster convergence. In this paper, we present a finer regret analysis that exactly characterizes this phenomenon by providing fast rates for the regret convergence. First, we show that given any estimate for the optimal quality function $Q^*$, the regret of the policy it defines converges at a rate given by the exponentiation of the $Q^*$-estimate's pointwise convergence rate, thus speeding it up. The level of exponentiation depends on the level of noise in the decision-making problem, rather than the estimation problem. We establish such noise levels for linear and tabular MDPs as examples. Second, we provide new analyses of FQI and Bellman residual minimization to establish the correct pointwise convergence guarantees. As specific cases, our results imply $O(1/n)$ regret rates in linear cases and $\exp(-\Omega(n))$ regret rates in tabular cases.

Fast Rates for Contextual Linear Optimization

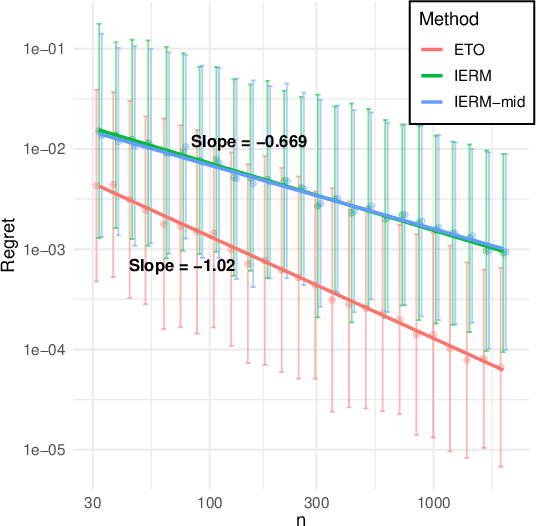
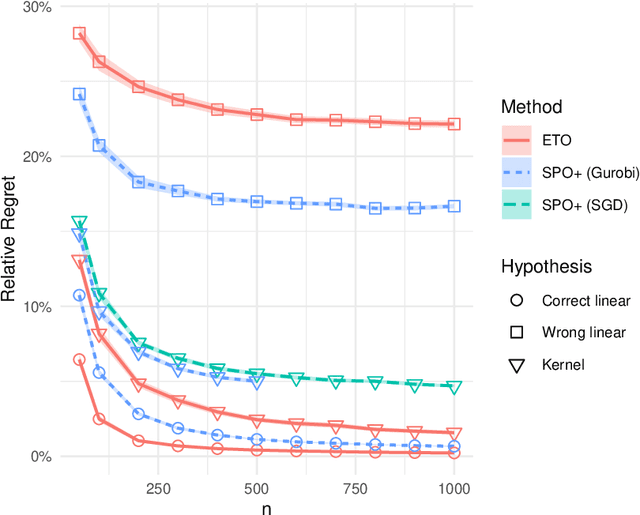
Incorporating side observations of predictive features can help reduce uncertainty in operational decision making, but it also requires we tackle a potentially complex predictive relationship. Although one may use a variety of off-the-shelf machine learning methods to learn a predictive model and then plug it into our decision-making problem, a variety of recent work has instead advocated integrating estimation and optimization by taking into consideration downstream decision performance. Surprisingly, in the case of contextual linear optimization, we show that the naive plug-in approach actually achieves regret convergence rates that are significantly faster than the best-possible by methods that directly optimize down-stream decision performance. We show this by leveraging the fact that specific problem instances do not have arbitrarily bad near-degeneracy. While there are other pros and cons to consider as we discuss, our results highlight a very nuanced landscape for the enterprise to integrate estimation and optimization.

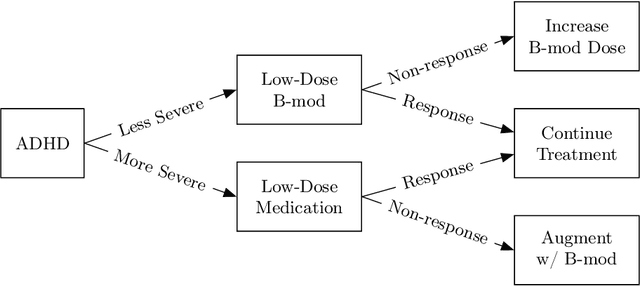
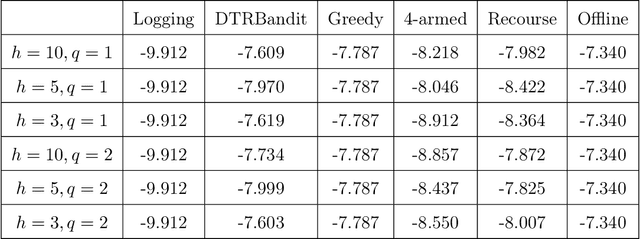
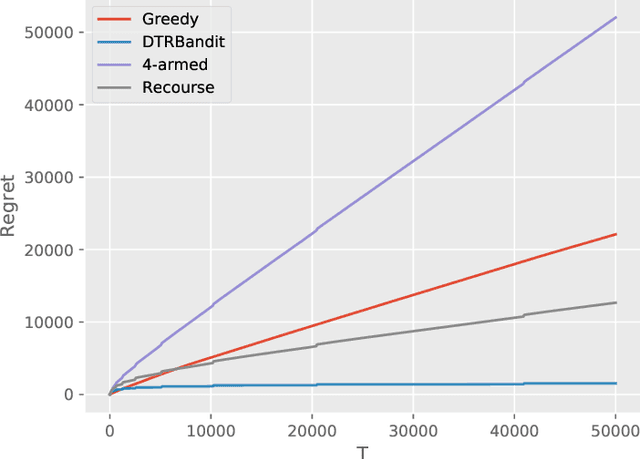
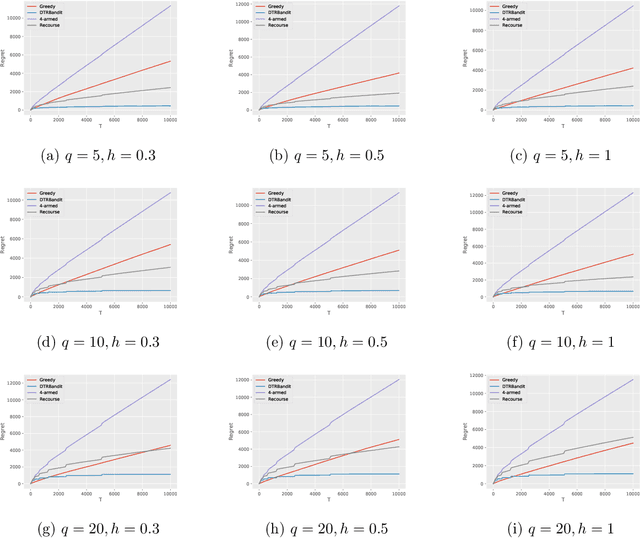
DTR Bandit: Learning to Make Response-Adaptive Decisions With Low Regret

Dynamic treatment regimes (DTRs) are personalized, adaptive, multi-stage treatment plans that adapt treatment decisions both to an individual's initial features and to intermediate outcomes and features at each subsequent stage, which are affected by decisions in prior stages. Examples include personalized first- and second-line treatments of chronic conditions like diabetes, cancer, and depression, which adapt to patient response to first-line treatment, disease progression, and individual characteristics. While existing literature mostly focuses on estimating the optimal DTR from offline data such as from sequentially randomized trials, we study the problem of developing the optimal DTR in an online manner, where the interaction with each individual affect both our cumulative reward and our data collection for future learning. We term this the DTR bandit problem. We propose a novel algorithm that, by carefully balancing exploration and exploitation, is guaranteed to achieve rate-optimal regret when the transition and reward models are linear. We demonstrate our algorithm and its benefits both in synthetic experiments and in a case study of adaptive treatment of major depressive disorder using real-world data.

Smooth Contextual Bandits: Bridging the Parametric and Non-differentiable Regret Regimes

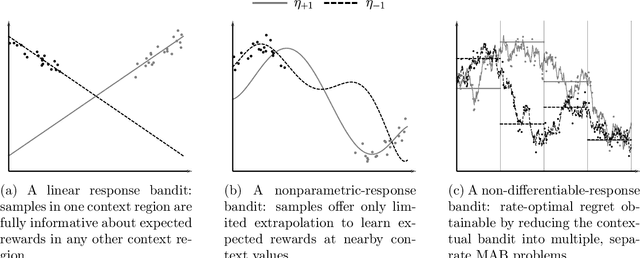
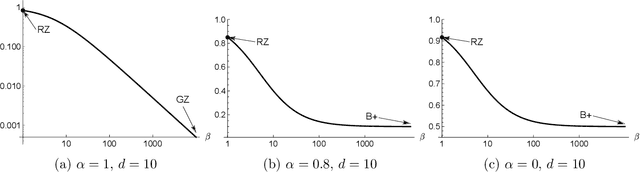
We study a nonparametric contextual bandit problem where the expected reward functions belong to a H\"older class with smoothness parameter $\beta$. We show how this interpolates between two extremes that were previously studied in isolation: non-differentiable bandits ($\beta\leq1$), where rate-optimal regret is achieved by running separate non-contextual bandits in different context regions, and parametric-response bandits ($\beta=\infty$), where rate-optimal regret can be achieved with minimal or no exploration due to infinite extrapolatability. We develop a novel algorithm that carefully adjusts to all smoothness settings and we prove its regret is rate-optimal by establishing matching upper and lower bounds, recovering the existing results at the two extremes. In this sense, our work bridges the gap between the existing literature on parametric and non-differentiable contextual bandit problems and between bandit algorithms that exclusively use global or local information, shedding light on the crucial interplay of complexity and regret in contextual bandits.