Wotao Yin
Zeroth-Order Regularized Optimization (ZORO): Approximately Sparse Gradients and Adaptive Sampling
Mar 29, 2020


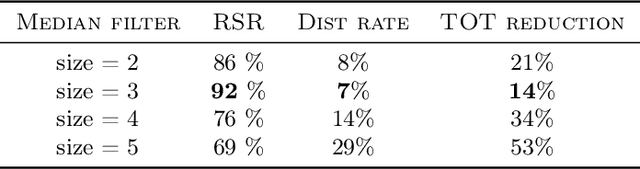
Abstract:We consider the problem of minimizing a high-dimensional objective function, which may include a regularization term, using (possibly noisy) evaluations of the function. Such optimization is also called derivative-free, zeroth-order, or black-box optimization. We propose a new $\textbf{Z}$eroth-$\textbf{O}$rder $\textbf{R}$egularized $\textbf{O}$ptimization method, dubbed ZORO. When the underlying gradient is approximately sparse at an iterate, ZORO needs very few objective function evaluations to obtain a new iterate that decreases the objective function. We achieve this with an adaptive, randomized gradient estimator, followed by an inexact proximal-gradient scheme. Under a novel approximately sparse gradient assumption and various different convex settings, we show the (theoretical and empirical) convergence rate of ZORO is only logarithmically dependent on the problem dimension. Numerical experiments show that ZORO outperforms the existing methods with similar assumptions, on both synthetic and real datasets.
Provably Efficient Exploration for RL with Unsupervised Learning
Mar 15, 2020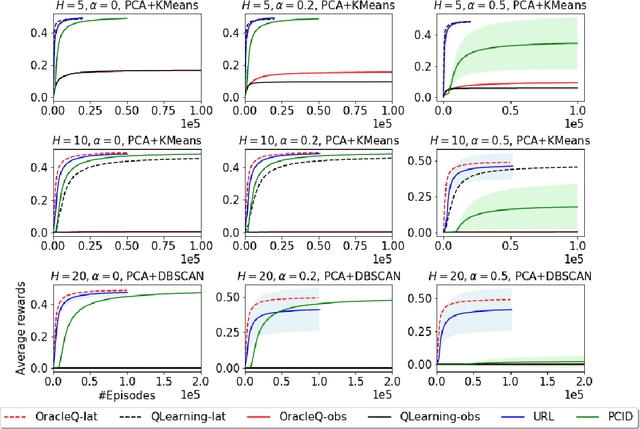
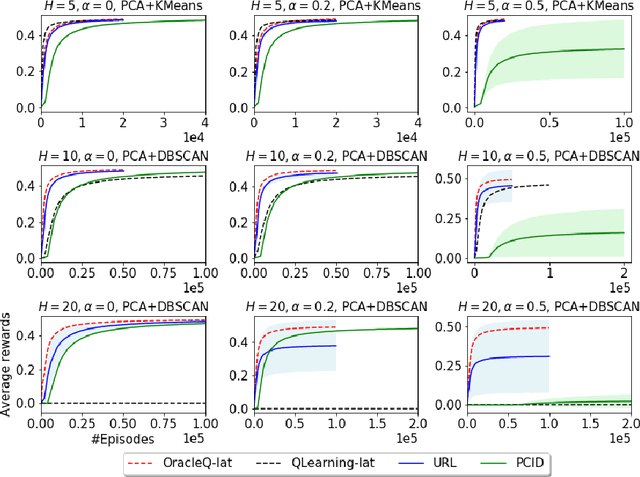
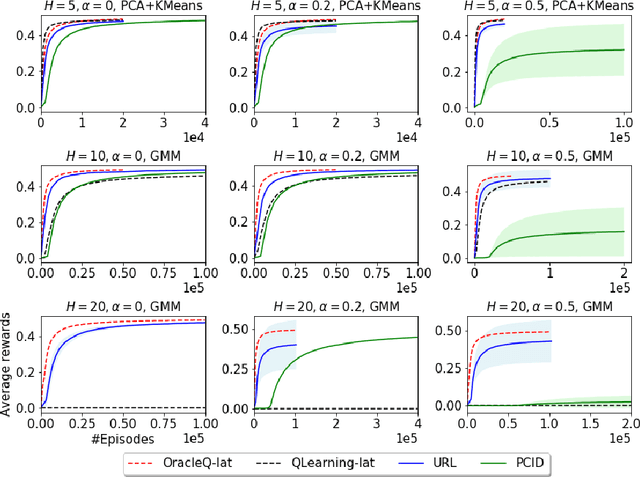
Abstract:We study how to use unsupervised learning for efficient exploration in reinforcement learning with rich observations generated from a small number of latent states. We present a novel algorithmic framework that is built upon two components: an unsupervised learning algorithm and a no-regret reinforcement learning algorithm. We show that our algorithm provably finds a near-optimal policy with sample complexity polynomial in the number of latent states, which is significantly smaller than the number of possible observations. Our result gives theoretical justification to the prevailing paradigm of using unsupervised learning for efficient exploration [tang2017exploration,bellemare2016unifying].
Safeguarded Learned Convex Optimization
Mar 04, 2020
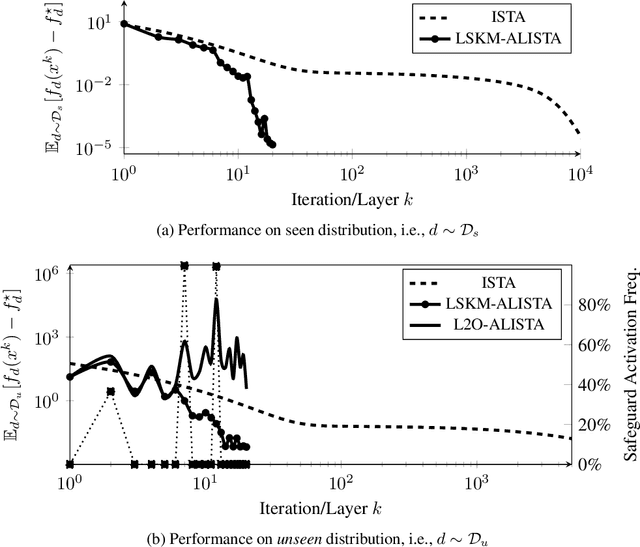
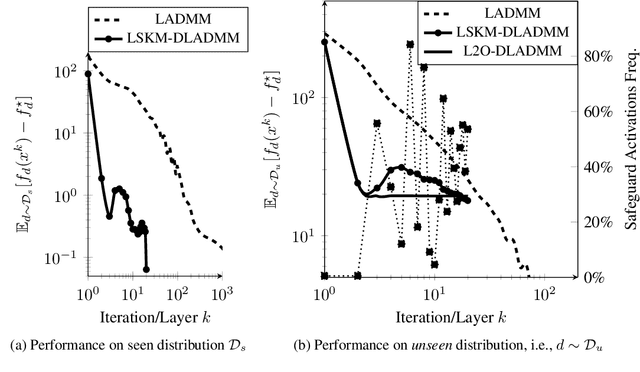

Abstract:Many applications require repeatedly solving a certain type of optimization problem, each time with new (but similar) data. Data-driven algorithms can "learn to optimize" (L2O) with much fewer iterations and with similar cost per iteration as general-purpose optimization algorithms. L2O algorithms are often derived from general-purpose algorithms, but with the inclusion of (possibly many) tunable parameters. Exceptional performance has been demonstrated when the parameters are optimized for a particular distribution of data. Unfortunately, it is impossible to ensure all L2O algorithms always converge to a solution. However, we present a framework that uses L2O updates together with a safeguard to guarantee convergence for convex problems with proximal and/or gradient oracles. The safeguard is simple and computationally cheap to implement, and it should be activated only when the current L2O updates would perform poorly or appear to diverge. This approach yields the numerical benefits of employing machine learning methods to create rapid L2O algorithms while still guaranteeing convergence. Our numerical examples demonstrate the efficacy of this approach for existing and new L2O schemes.
LASG: Lazily Aggregated Stochastic Gradients for Communication-Efficient Distributed Learning
Feb 26, 2020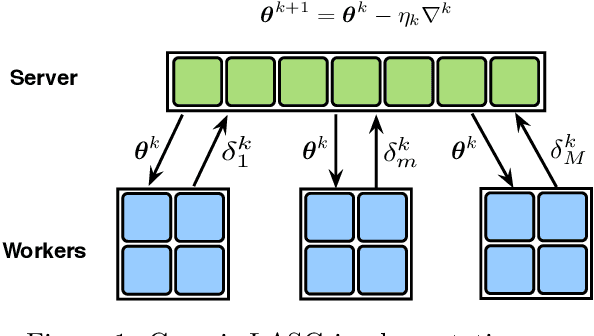
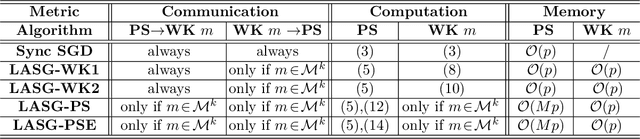
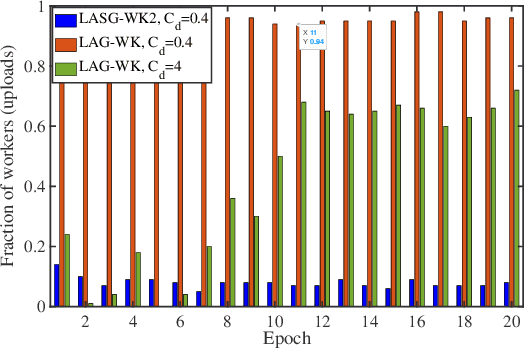

Abstract:This paper targets solving distributed machine learning problems such as federated learning in a communication-efficient fashion. A class of new stochastic gradient descent (SGD) approaches have been developed, which can be viewed as the stochastic generalization to the recently developed lazily aggregated gradient (LAG) method --- justifying the name LASG. LAG adaptively predicts the contribution of each round of communication and chooses only the significant ones to perform. It saves communication while also maintains the rate of convergence. However, LAG only works with deterministic gradients, and applying it to stochastic gradients yields poor performance. The key components of LASG are a set of new rules tailored for stochastic gradients that can be implemented either to save download, upload, or both. The new algorithms adaptively choose between fresh and stale stochastic gradients and have convergence rates comparable to the original SGD. LASG achieves impressive empirical performance --- it typically saves total communication by an order of magnitude.
Does Knowledge Transfer Always Help to Learn a Better Policy?
Dec 06, 2019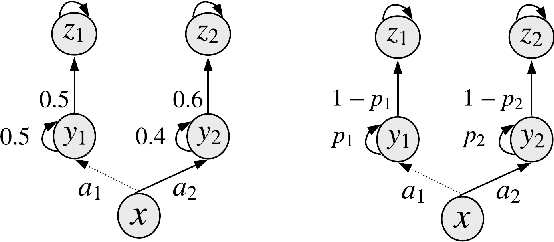
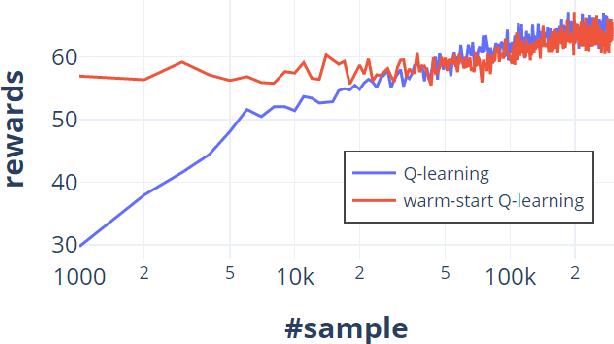
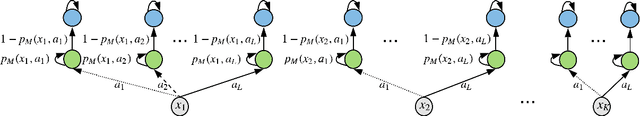
Abstract:One of the key approaches to save samples when learning a policy for a reinforcement learning problem is to use knowledge from an approximate model such as its simulator. However, does knowledge transfer from approximate models always help to learn a better policy? Despite numerous empirical studies of transfer reinforcement learning, an answer to this question is still elusive. In this paper, we provide a strong negative result, showing that even the full knowledge of an approximate model may not help reduce the number of samples for learning an accurate policy of the true model. We construct an example of reinforcement learning models and show that the complexity with or without knowledge transfer has the same order. On the bright side, effective knowledge transferring is still possible under additional assumptions. In particular, we demonstrate that knowing the (linear) bases of the true model significantly reduces the number of samples for learning an accurate policy.
XPipe: Efficient Pipeline Model Parallelism for Multi-GPU DNN Training
Nov 20, 2019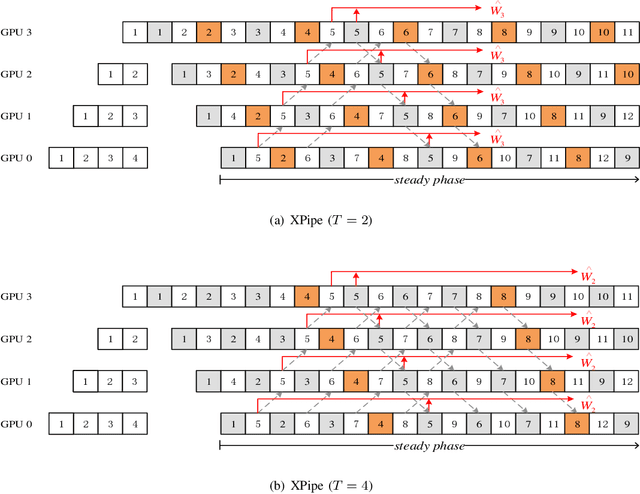
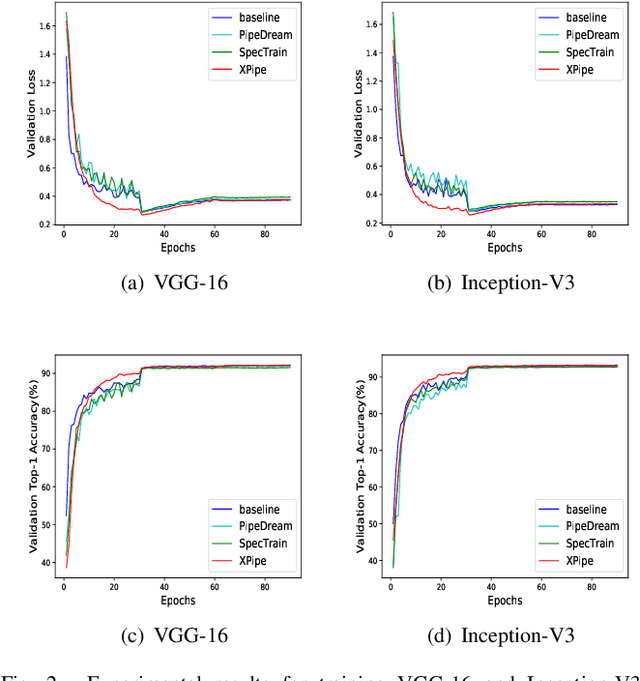
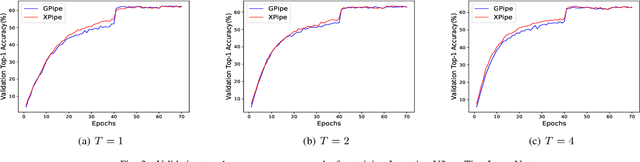
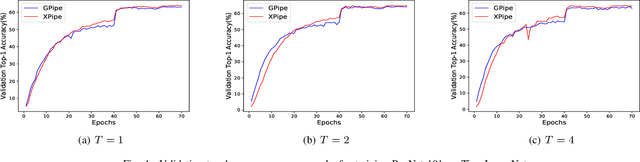
Abstract:We propose XPipe, an efficient asynchronous pipeline model parallelism approach for multi-GPU DNN training. XPipe is designed to make use of multiple GPUs to concurrently and continuously train different parts of a DNN model. To improve GPU utilization and achieve high throughput, it splits a mini-batch into a set of micro-batches and allows the overlapping of the pipelines of multiple micro-batches, including those belonging to different mini-batches. Most importantly, the novel weight prediction strategy adopted by XPipe enables it to effectively address the weight inconsistency and staleness issues incurred by the asynchronous pipeline parallelism. As a result, XPipe incorporates the advantages of both synchronous and asynchronous pipeline model parallelism approaches. Concretely, it can achieve very comparable (even slightly better) model accuracy as its synchronous counterpart, while obtaining higher throughput than it. Experimental results show that XPipe outperforms other state-of-the-art synchronous and asynchronous model parallelism approaches.
ODE Analysis of Stochastic Gradient Methods with Optimism and Anchoring for Minimax Problems and GANs
Jun 06, 2019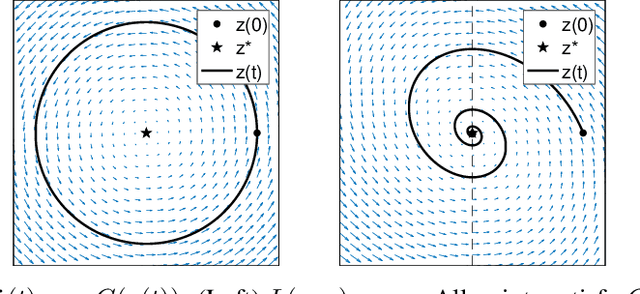


Abstract:Despite remarkable empirical success, the training dynamics of generative adversarial networks (GAN), which involves solving a minimax game using stochastic gradients, is still poorly understood. In this work, we analyze last-iterate convergence of simultaneous gradient descent (simGD) and its variants under the assumption of convex-concavity, guided by a continuous-time analysis with differential equations. First, we show that simGD, as is, converges with stochastic sub-gradients under strict convexity in the primal variable. Second, we generalize optimistic simGD to accommodate an optimism rate separate from the learning rate and show its convergence with full gradients. Finally, we present anchored simGD, a new method, and show convergence with stochastic subgradients.
Plug-and-Play Methods Provably Converge with Properly Trained Denoisers
May 14, 2019
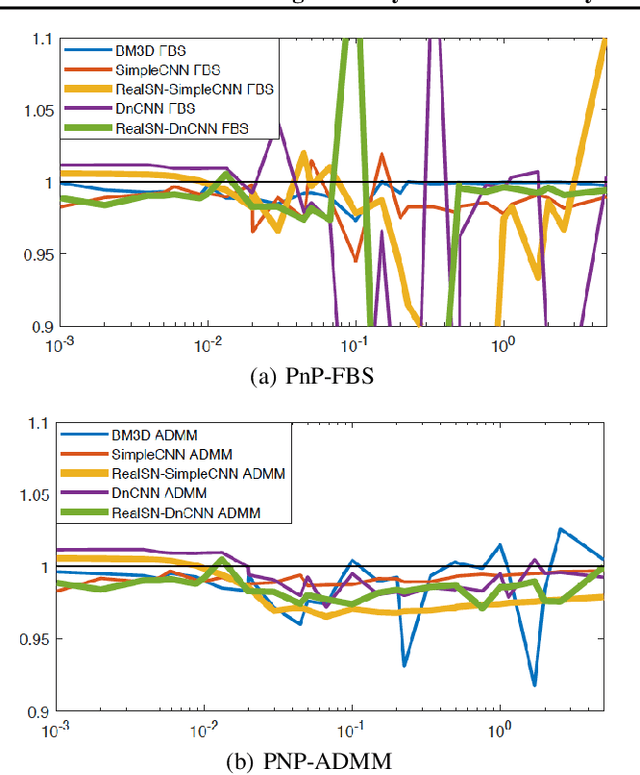

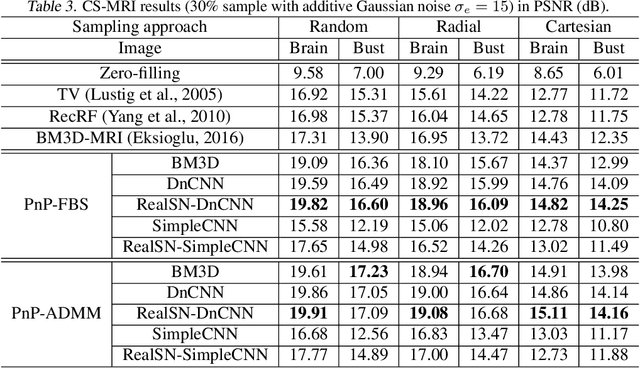
Abstract:Plug-and-play (PnP) is a non-convex framework that integrates modern denoising priors, such as BM3D or deep learning-based denoisers, into ADMM or other proximal algorithms. An advantage of PnP is that one can use pre-trained denoisers when there is not sufficient data for end-to-end training. Although PnP has been recently studied extensively with great empirical success, theoretical analysis addressing even the most basic question of convergence has been insufficient. In this paper, we theoretically establish convergence of PnP-FBS and PnP-ADMM, without using diminishing stepsizes, under a certain Lipschitz condition on the denoisers. We then propose real spectral normalization, a technique for training deep learning-based denoisers to satisfy the proposed Lipschitz condition. Finally, we present experimental results validating the theory.
ExtraPush for convex smooth decentralized optimization over directed networks
Jan 30, 2019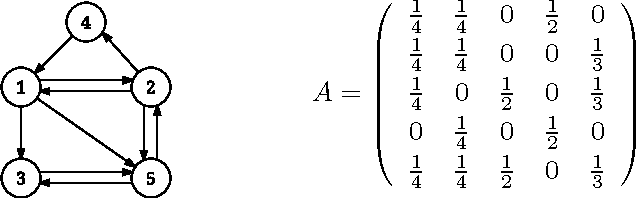
Abstract:In this note, we extend the algorithms Extra and subgradient-push to a new algorithm ExtraPush for consensus optimization with convex differentiable objective functions over a directed network. When the stationary distribution of the network can be computed in advance}, we propose a simplified algorithm called Normalized ExtraPush. Just like Extra, both ExtraPush and Normalized ExtraPush can iterate with a fixed step size. But unlike Extra, they can take a column-stochastic mixing matrix, which is not necessarily doubly stochastic. Therefore, they remove the undirected-network restriction of Extra. Subgradient-push, while also works for directed networks, is slower on the same type of problem because it must use a sequence of diminishing step sizes. We present preliminary analysis for ExtraPush under a bounded sequence assumption. For Normalized ExtraPush, we show that it naturally produces a bounded, linearly convergent sequence provided that the objective function is strongly convex. In our numerical experiments, ExtraPush and Normalized ExtraPush performed similarly well. They are significantly faster than subgradient-push, even when we hand-optimize the step sizes for the latter.
* 16 pages, 3 figures
AsyncQVI: Asynchronous-Parallel Q-Value Iteration for Reinforcement Learning with Near-Optimal Sample Complexity
Dec 03, 2018
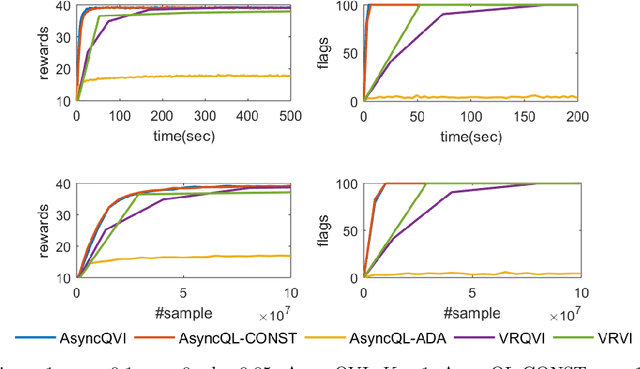

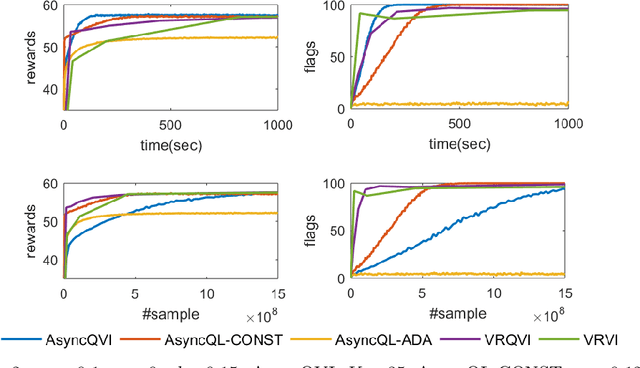
Abstract:In this paper, we propose AsyncQVI: Asynchronous-Parallel Q-value Iteration to solve Reinforcement Learning (RL) problems. Given an RL problem with $|\mathcal{S}|$ states, $|\mathcal{A}|$ actions, and a discounted factor $\gamma\in(0,1)$, AsyncQVI returns an $\varepsilon$-optimal policy with probability at least $1-\delta$ at the sample complexity $$\tilde{\mathcal{O}}\bigg(\frac{|\mathcal{S}||\mathcal{A}|}{(1-\gamma)^5\varepsilon^2}\log\Big(\frac{1}{\delta}\Big)\bigg).$$ AsyncQVI is the first asynchronous-parallel RL algorithm with convergence rate analysis and an explicit sample complexity. The above sample complexity of AsyncQVI nearly matches the lower bound. Furthermore, AsyncQVI is scalable since it has low memory footprint at $\mathcal{O}(|\mathcal{S}|)$ and also has an efficient asynchronous-parallel implementation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge